- 收藏
- 加入书签
基于改进的灰色理论和BP神经网络组合算法的小样本质量预测研究
摘要:电机行业产品具有小样本生产环境和加工质量数据具有趋势性和随机性的特点,灰色理论在小样本情况预测的优势和BP神经网络在非线性、随机性方面拟合的优点,两种模式优势互补。因此,提出改进的灰色理论和BP神经网络组合的质量预测模型,并通过比较各种预测方法来验证组合预测模式的准确性和有效性。
关键词:灰色理论 BP神经网络 质量预测
中图分类号:TP391 文献标识码:A
1引言
电机行业的产品具有多规格、小批量的特点,质量控制的要求和难度就更高,传统的统计过程控制(SPC)控制图虽然能够起良好的质量监控作用,但对小批量、多品种的柔性生产模式适应能力不强;同时还有一定的滞后性,不能有效的防止不合格品的产生。传统的SPC质量控制技术已不能适应质量控制的需要,也很难满足零废品率、高质量控制的要求。为了在单件小批量环境中实现零缺陷控制,必须使用基于质量预测的质量控制手段。
结合灰色理论在小样本情况预测的优势和BP神经网络在非线性、随机性方面拟合的优点,提出一种质量预测思路:把已加工的历史数据作为模型的输出,运用灰色理论和人工智能的技术手段,对未来下一时刻的质量值进行预测建模,提前获知下一时刻的质量状况,真正做到事前预防,提前消除质量隐患。
2 灰色理论数学原理
华中科技大学邓聚龙教授提出灰色理论,专门用于研究具有不确定性的灰色系统的预测,小批量生产条件下电机零部件加工工序的质量预测属于典型“小样本,少信息”的灰色系统。灰色理论预测模型的优点是当所需样本量较小时,系统的预测精度较高,但其基于指数函数的预测没有考虑系统的随机性,所以随机误差预测精度较差。
3 BP神经网络数学原理
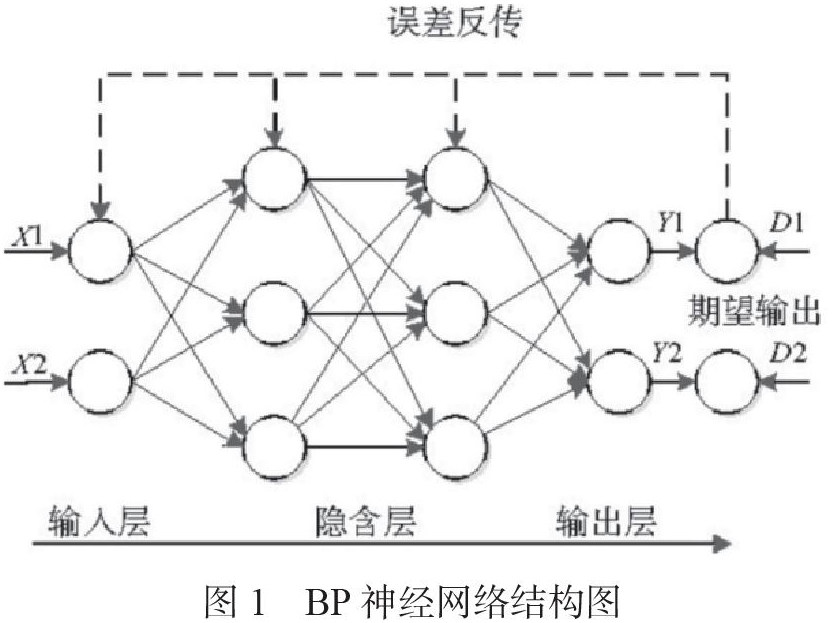
BP神经网络(Back Propagation)是使用得最为广泛的第二代神经网络模型,包括输入层(input)、隐含层(hidden layer)和输出层(output layer)。其结构图如图1所示:
在BP神经网络中,确定了输入层和输出层中的节点数,但隐藏层节点的的层数和数量是不确定的。实际上,隐藏层节点的数量对神经网络的性能有影响,有一个经验公式15,可以确定隐含层节点数目,如下:
其中h是隐含层节点的数量,m是输入层节点的数量数目,n是输出层节点的数量,a是1~10之间的调整常数。
BP神经网络由两个过程组成,信息的正向传导和误差的反向传导。输入层节点中的每个神经元负责接收来自外界的输入信息并将其发送到隐藏层中的每个神经元;隐藏层负责内部信息的处理和转换并传递输出层中每个神经元的信息,并在通过激励函数后,完成信息的前向传播,当输出层信息输出到外部并与实际输出进行对比,与预期输出产生的误差将会进入反向传播阶段。通过输出层校正误差,并且根据误差梯度校正每层的权重和阈值,并且逐层地反向传输隐藏层和输入层。网络训练过程就是信息正向传播和误差反向传播时调整各个节点权重值,该过程直到网络输出中的误差降低到可接受的水平或预定的学习次数。
4 基于灰色理论和BP神经网络的组合算法
为了提高预测精度,通过采用新陈代谢来改进GM(1,1)预测模型,即删除最旧的信息并输入最新信息以形成滚动样本集。这种方法在一定程度上提高了预测精度,但毕竟该模型是建立在部分信息而不是全部信息的的基础上,预测值和实际值之间的残差是预测准确性的根本原因。因此,通过BP神经网络校正灰色预测模型的残差值可以获得更准确的预测值。其主要过程如下所示:
(1)建立残差序列的BP神经网络模型
残差是t时刻的原始数据序列与灰色预测模型模拟值之间的差值,记为。为了预测t+1时刻的残差,将n个时刻的残差作为BP神经网络的输入样本,神经网络的输出则为t+1时刻的残差。
(2)运用BP神经网络模型进行训练
收集足够数量的残差序列,并通过上述BP神经网络算法训练网络,使得不同的输入向量获得相应输出值,将训练好的网络用于预测残差序列。
(3)获得新的预测值
由BP网络预测的t+1时刻的残差序列加上灰色模型模拟的就是t+1时刻的最终预测值,如式23所示:
参考文献
[1]董辉,赵刚,单忠臣,陈杰远.基于灰色理论和神经网络的零件尺寸精度的组合预报[J].应用科技,2015(06):48-49.
[2]张爽,李辉.经济视角下质量预测的BP神经网络优化方法研究[J].现代制造工程,2018(05):1-2+11.




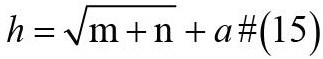 < a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/afkj/afkj202114/afkj202114312-3-l.jpg">
< a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/afkj/afkj202114/afkj202114312-3-l.jpg">

 京公网安备 11011302003690号
京公网安备 11011302003690号

