- 收藏
- 加入书签
基于长方形面积计算公式的小学教学中化归思想方法的渗透
【摘要】目前,我国对于教育行业提出培养学生全面发展的新要求。在这样的时代背景下需要教师注重培养学生的数学思维品质,化归思想方法有利于培养学生多方面的能力和提高小学数学整体教学水平。本文以长方形面积计算的启发式教学为例对小学数学化归思想方法的渗透展开探讨研究。
【关键词】小学数学;化归思想方法;教学应用
一、引言
通过对比小学初中高中的课标,笔者发现无论是小学还是中学都涉及到了图形与几何,小学初中讲平面几何初高中讲立体几何。不同点在于抽象的程度不一样,这也是大多数学生认为数学越学越难的原因。因此,从小学就将化归的思想方法渗透给学生,一定程度上能增加学生的数学学习的自信心和兴趣,打破学生的常规思维方式,也为后续的学习奠定了基础。
二、化归思想与化归方法的内涵及意义
化归思想的内涵主要是“转化”与“归结”。化归思想方法的教学不仅有利于培养小学生的解题能力而且对初高中甚至大学的数学学习同样重要。“授人以鱼不如授人以渔”。数学老师在课堂教学中渗透化归的数学思想,才能真正意义上拓宽学生的解题思路,提高学生的思维能力,增强解题能力。化归思想方法的使用,还注重学生发散思维和创新思维的培养,注重形成科学的数学知识体系,把复杂的问题简单化,将其转化为以前熟悉的问题,用已有知识和方法来解决,提升小学生的核心素养和数学素质。
三、化归思想在小学数学教学中的应用
(一)在动手操作中体验化归思想
本文以长方形、平行四边形面积计算方法为例,运用化归的数学思想,把学生已经学会的正方形的计算方法运用到长方形、平行四边形的计算过程中,从而让学生清楚地了解面积公式的推导过程,构建和完善他们的认知结构。
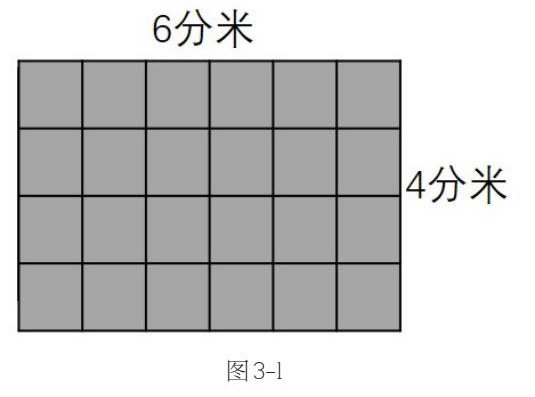
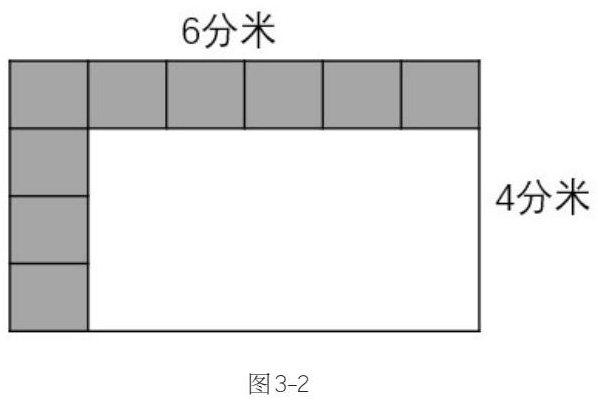
在学习长方形面积的计算时,很多同学已经知道了长方形面积计算公式为长宽,但仍然有的学生对其存有疑虑,不知道为什么两个线段相乘就是面积,会提出面积是线的疑虑。还有的学生会问原来写的答案的单位是分米,为什么现在变为了平方分米。由于学生经过之前的学习已知边长为1分米的方格的面积为1平方分米,所以针对学生的这两个问题,教师可以利用教室已有的条件如课桌让学生用一平方分米的方格来将其摆满,通过让学生数方格的个数的方式认识长方形的面积计算公式,如学生用方格摆满课桌(如图3-1所示)。通过数方格的个数(24个)学生可以知道课桌的面积为24平方分米,教师再引导学生只摆课桌的长和宽(如图3-2所示),让学生去发现其中的规律,进而得出面积的计算公式。
小学阶段的学生的抽象思维水平不高,常需要教师设计让学生自己动手操作的教学活动。本节教学思路是以学生已知的边长为1分米的正方形的面积为1平方分米的旧知为出发点,让学生测量具体的实物,测量方式由摆满方格到只摆部分方格。教师将化归的思想方法渗入其中,把抽象的面积计算公式转化为具体可感的事物让学生清楚地了解面积公式的推导过程,从而发现化归思想方法的运用,形成初步认识。
(二)知识梳理,深化化归思想方法
为将化归思想进一步渗透给学生,教师可以继续抓住在学习长方形面积探究这一核心概念,先引导学生回忆和思考长方形面积计算公式中的长和宽的意思以及求长方形的面积本质是在求什么(图3-3)。接着带领学生在方格中探究平行四边形的面积(图3-4),以度量单位为核心进行学习的迁移,通过寻找度量单位个数的方法,概括新旧知识间的共同本质,有意识地沟通新旧知识间的联系,在迁移中帮助学生理解面积的意义。
教师在课堂上引导学生了解知识结构,培养学生在探索新知识的过程中会运用旧知识的能力能增强独立思考能力,提高有效整合、储存新旧知识的能力。
(三)适时点拨内化化归思想
知识的教授要课上与课下巩固练习相结合。在教授解题方法之后教师要安排相同类型的题目让学生解答,比如结合化归在图形与几何的相关知识点,就可以布置学生思考直角梯形面积求解,等腰梯形面积求解以及一般梯形的面积计算方法。学生在充分认识了长方形,三角形的面积计算公式后,教师可以进一步提出新的解题方法如等腰三角形可以分成一个长方形和两个三角形,进一步提高学生知识的运用能力。
应用举例如图3-5和3-6所示
学生通过前面的学习有了计算规则图形面积的基础之后教师布置学生做上面的变式,将化归思想继续渗透给学生。第一题(图3-5)求空白部分的面积。此题可视为把一张长方形的纸折一个角,空白部分的面积为外面大的长方形的面积减去折角部分的两个三角形的面积。第二题(图3-6)求阴影部分面积。观察图形可知,用两个正方形的面积减去空白部分的两个三角形的面积就是阴影部分的面积。
四、对小学教师渗透化归思想方法的几点建议
教师要转变数学内容的教育方式和选择教学内容的标准要将数学内容通过整理系统化的教授给学生,让学生通过掌握一道题而会一类题,从而使学生潜移默化了解化归思想。另外,教师要利用转换的思想鼓励学生主动根据不同的类型和内容整理知识,学会自我总结本章的学习重点。值得强调的一点是,在双减政策的时代背景下,注重培养学生能力,而不是增加学生压力,因此,教师给学生的作业应在精不在多。
教师在开展具体课程时要以学生为主,发挥学生的主体作用,多考虑学生的思维,而不仅是按自己的思维进行讲解,让学生通过自己思考问题提高他们自己运用化归思想的能力。数学的思想渗透比教授知识更为重要。教学最终结果的参考不是教师在课堂中讲了多少,而是学生学了多少知识。在数学核心素养培养中更是应当把学生的长远发展放到首位,通过自主学习发现,让学生主动建构数学知识,深刻体会数学思想。
教师应跟随新课标的导向,一方面要努力挖掘教材中可以体现化归思想的教学内容,通过长期渗透体会化归思想方法;另一方面应该从多角度、多维度渗入化归思想,培养学生的思维能力和学习能力。数学教师应当积极利用数学教学资源,开展有效的数学教学活动,逐步实现小学生的核心素养的培养。
五、结束语
德国教育家第斯多惠说:“一个坏教师给学生奉献真理,一个好老师则教学生发现真理。”因此,在教学中教师要重视对学生思维的培养,加强对学生化归思想的渗透,让学生会一道题就会一类题,注重从本质上提高学生能力,这也是积极响应国家双减政策的一种方式。
【参考文献】
[1]史久一.化归与归纳类比联想[M].大连理工大学出版社,2008:1-2.
[2]李西华.运用化归思想方法教学的意义[J].课程教学教材研究.中教研究2019.9~10:5.
[3]冯桂群.数学“三动”课堂:让能动学习自然发生[J].小学数学教与学,2021.10:36-38.
[4]马芯兰 孙佳威.开启学生的数学思维.[M].北京师范大学出版社,2021:32-33.
[5]邵凡玲.小学数学“图形与几何”教学中化归思想的渗透研究.[D].2018:4.
[6]洑冬青.对小学数学运用化归思想方法的分析[J].学周刊.2018 (28):96.
【作者简介】
余庆雯(2000~),女,汉族,重庆市忠县,本科,研究方向:数学与应用数学。




 < a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/528d/528d202201/528d202201215-3-l.jpg">
< a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/528d/528d202201/528d202201215-3-l.jpg"> < a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/528d/528d202201/528d202201215-4-l.jpg">
< a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/528d/528d202201/528d202201215-4-l.jpg">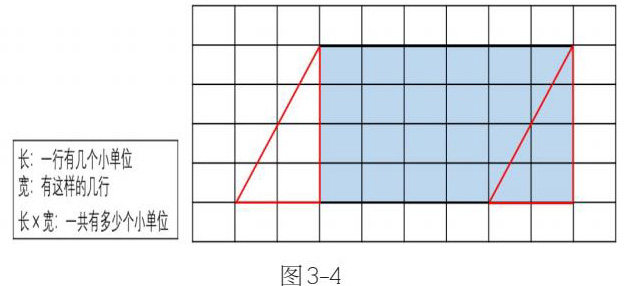 < a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/528d/528d202201/528d202201215-5-l.jpg">
< a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/528d/528d202201/528d202201215-5-l.jpg">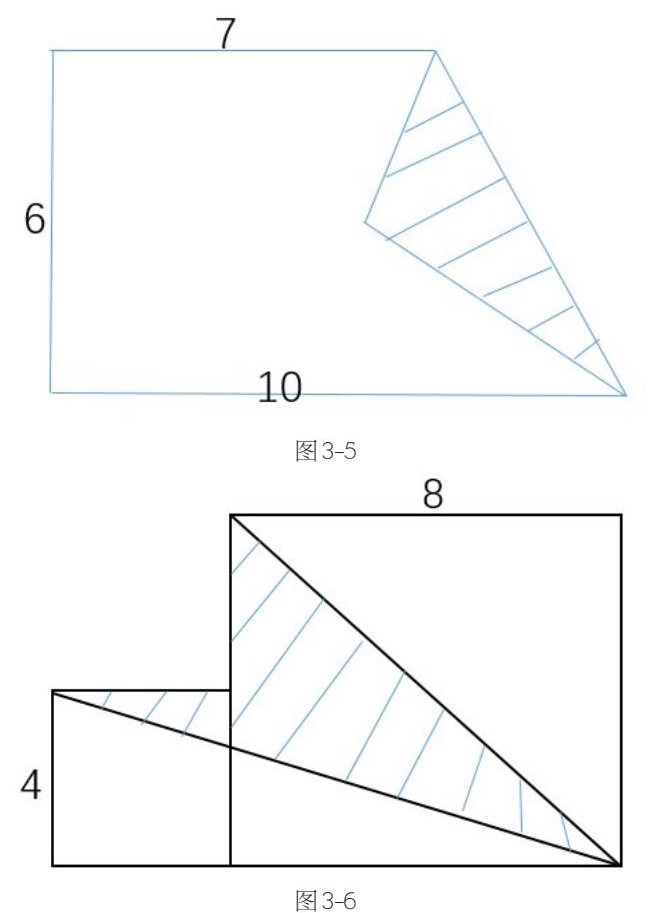

 京公网安备 11011302003690号
京公网安备 11011302003690号

