整体构思在浮力题中的应用

炫动漫

重庆市巴蜀渝东中学?404600

打开文本图片集

浮力教学在初中阶段物理中具有重大作用，在重庆中考中也占有重要的比例，本可以很好的培养学生物理思维，但是浮力题型涉及力与运动、密度、液体压强、固体压强等综合问题，学生往往感到一片茫然，甚至谈"浮"色变。为此，这就对老师的教学方法提出了更多的要求，教学方法老师需要采用确实可行的方式，将难点的问题简易化方便培养学生系统的逻辑思维能力，培养学生能够自我归纳、总结，实现多题一解，获得举一反三的能力，通过这种教学方法的采用促进学生在日后物理学习过程中迈向更高台阶，为高中物理的学习打下坚实的基础。整体的思维方法能够有效果的从部分到整体，将复杂问题简易化，不需要将多个物体及多个细小的过程作为重点来分析，而是追求全面把握，不再让学生感到无从下手，降低了审题难度，提高解题效率，同时也简化了解题的过程，更好的培养了学生的逻辑思维能力。

一整体法巧解浮力压强综合题型：

浮力对于初中学生感到困难的最大特点来源于综合性太强，需要涉及的知识点以及其中的联系把握不住，而整体法从整体入手简化过程，有效的减少学生思维的难度，从最简单基础的推导，循序渐进的去找到其中的内在联系，使看似困难的题迎刃而解。

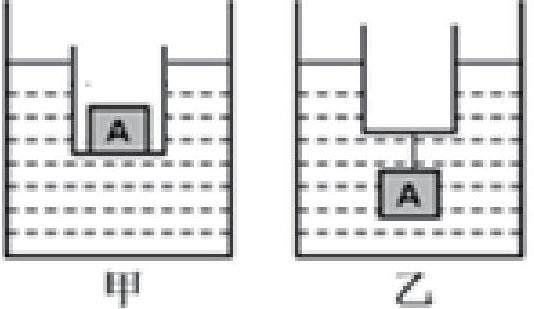
例1：如下图所示，两容器中装有一定质量的水，先后将甲、乙两种方式使物体A和小玻璃杯漂浮在水面上，（图中细线重力及体积均不计）．设甲、乙两图中物体A和小玻璃杯共同受到的浮力，分别为F甲和F乙，水对容器底的压强分别为p甲和p乙，则（）

A．p甲=p乙；F甲＜F乙；

B．p甲=p乙；F甲=F乙

C．p甲＜p乙；F甲=F乙；

D．p甲＞p乙；F甲＞F乙；

思路分析：由图可知物体都处于漂浮状态，要比较甲、乙，F甲、F乙的大小，可利用物体的浮沉条件进行判断、比较．由P=ρ液gh；容器底部受到压强的水，还与深度有关的水，当容器底面积不发生变时，若物体排开水的体积就越来越大时，液体表面就越高，容器的底部受到的压强就越来越大．

把A和容器看作一个整体，则A和容器的总的重力保持不变，由图中可分析出物体都是浮在水面上的，所以甲、乙两个图中物体A和小玻璃杯一起共同受到的浮力，一定等于物体A和小玻璃杯的总重力大小不变，所以F甲=F乙；

因为在这两中情况下能判断出浮力是相等的，又由阿基米德原理又可分析得出，F浮=ρ水gv排；

∵F乙=F甲，∴v排乙=v排甲；

由甲、乙两图得，液体表面的高度是相等的情况下，由公式p=ρgh可得，当ρ一不变的情况下，若h相等，则P不变；即 p乙=p甲．所以选择答案B．

二整体构思在液面升降问题上的应用：

液面升降问题对于初中学生也是感到困难的题型，不同物理量之间的变换将学生搞得晕头转向，抓住整体从受力的方向分析浮力，再通过浮力的变化找到液体排开体积的变化的多少，便可解决液面升降问题。

例2：如图所示，小船上有三个a球。小船和小球一起漂浮在水面上，小球a的密度小于液体的密度。小球b的密度等于水的密度，小球c密度小于水的的密度，船可以在水面上自由的静止的漂浮。

（1）若将球a放入水中，然后将球a （填入浮沉情况），水面（填“升高”或“下降”或“不变”）。图5

（2）若将球b放入水中，然后将球b（填入浮沉情况），水面（填“升高”或“下降”或“不变”）。

（3）若只将球c放入水中，然后球cb（填入浮沉情况），水面（填“升高”或“下降”或“不变”）

（4）若同时将abc三球从船中取出放入水中，水面会（填“升高”或“下降”或“不变”）。

思路分析：根据浮力知识a球放入水中漂浮，b球悬浮于水中，c球浸入水中。当容器的底面积不变时，物体排出的水的体积越大，液面越高，液面的变化可以通过寻找V排的变化来判断。由F浮=ρ水gv排，找到浮力最终还是怎么变化。

将ABC及小船看作一个整体，当球A放在水里，像船一样漂浮。F浮= G总，总浮力不变，所以V排保持不变。液面不变;将放入水中B球F浮=G总，不变的是浮力故V排不变，液面将不变;将放入水中的C球F浮+F支=G总，总的重力不变，总的浮力减小故V排减小，液面下降。将ABC三个小球同时放入水中整体受力F浮+F支=G总，总的重力不变，总的浮力减小故V排减小，液面下降。

参考文献

[1]董兰.初中物理浮力教学难点及对策探索[J].中学生数理化学研版，2014（11）.

[2]王虎华.初中物理浮力问题的教学思考[J]. 新教育时代教师版，2016（14）.

[3]黄岑.整体法在初中物理解题中的应用分析[J]. 数理化学习教育理论版，2013（4）.

[4]徐广玉.整体分析法在初中物理解题中的应用[J]. 启迪与智慧教育版，2015（1）.

*本文暂不支持打印功能