- 收藏
- 加入书签
基于ARIMA预测模型的小批量物料的生产安排
摘要:电子产品企业面临着种种挑战,例如在不知物料所需量的情况下,如何合理安排多种类小批量物料的生产。本文采用时间序列中的 ARIMA 预测模型,进行预测以周为单位的物料需求量,并根据动态规划多方面因素考虑,合理制定生产计划。
关键词:最小二乘法 ARIMA 预测动态规划
引言:
随着经济的发展,人民生活水平的提高,顾客对产品的多样化要求越来越高。生产模式逐渐转向多品种小批量,这将导致更复杂的企业各方面管理。物料管理作为整个企业运作的重要环节,在成本控制方面占有主导地位,因此在多品种小批量模式下如何运转好物料管理的各个环节,具有十分重要的意义。
在当今快速多变、竞争日趋激烈的市场环境中,为了生存与发展,越来越多的企业采用了小批量多品种的生产方式来满足用户的需求。生产的模式已从大批量生产向小批量生产、个性化生产、定制式生产转变。市场环境的变化,批量小、多品种、短的交货期是企业面临的现实生存环境。传统的管理方式在面对计划变更频繁、紧急插单、交货延迟、成本上升方面显得束手无策。我们传统的制造企业为了生存下来,也必须作相应的改变。企业职能从社会的角度讲,是满足社会需求,为消费者提供所需的产品。从企业内部来看,制造型企业是在一定规则和信息的支持下对有形的物质进行加工组合的过程。所以,制造型企业的处理对象是各种物料。物料始终伴随着企业的各个生产活动过程。因此对物料的管理、存取、搬运、加工、装配就成为企业内车间生产活动的主要内容。车间生产效率的高低、成本的高低不仅与物料的消耗和物化劳动量有关,而且与物料的储存方式、存取效力、辅助人力消耗有关。当一个产品设计定型后,其基本材料消耗就确定了。但其生产效率却与物料的供给方式、存取方式、搬运方式有很大的关系。这个问题在我们的许多制造企业特别是传统的制造企业却给忽视了,没有得到应有的重视。
1.问题一模型的求解
1.1 选出 6 种重点关注的物料
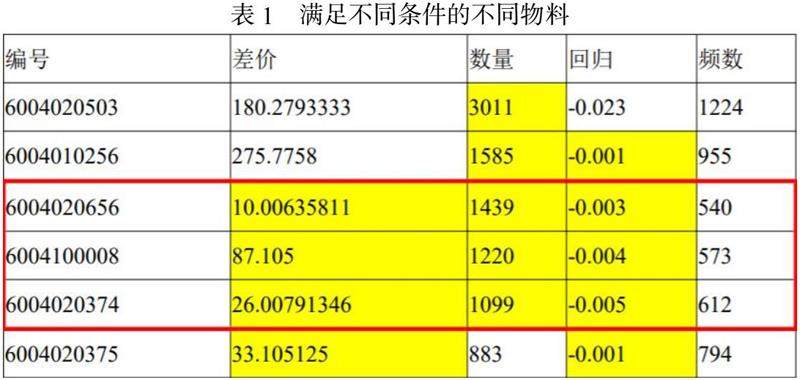
通过 SPSS 软件,将需求量及日期运用最小二乘法[1]得到各物料的回归系数,可认为回归系数B为总趋势,若系数为正,即随时间增长,市场需求量越大,负则反之,取回归系数大于-0.005的物料。其次,分别对表1中13种物料的需求量求和得到数量,取数量大于1000的物量,再分别对表1中13种物料销售单价[2]进行最大值最小值计算,得到差值,选取差值小于100的物料,如下表1所示:
最后,满足2条及以上条件的6种物料即为最终选择结果。由上表可知:共有8种物料满足2条及以上条件,共有3种物料满足3条条件。
第三步:对仅满足2条条件的5种物料进行筛选
首先,对频数进行比较得出:
6004020900>6004020504>60040209 18>6004020375>6004010256
1.2实验结果及分析
因所建模型为周预测模型[3],故排除历史数据中2022年5月后需求量的数据,即6004020900,根据物料的市场需求数量趋势及稳定性,筛选出6004020918、
6004020375两种物料。
为了进一步提升选择准确性,利用SPSS对数据进行主成分分析[4],经过次调试比对,选出最能反应实际情况的权重配比并取整,再对各项数据进行赋权求和,选取最优结果。
公式如下:
总权值= B2*(-25%)+C2* 25%+ D2 * 25%+ E2 * 25%
通过比较权值,结果如下:
6004020503>6004010256>6004020656>6004 100008>
6004020374>6004020375>6004010174>6004020918
最终,得出选择出应重点考虑的6种物料物料为:
6004020656、6004 100008、6004020374、6004020918、 6004020375、6004010256
2.问题二模型的求解
2.1实验求解
首先,由题中假设的对应关系得,本周的实际需求数等于上周的生产计划数,且本周生产计划数不可在本周使用,故以动态规划算法求解。根据问题一的周预测模型预测出101-177周的需求量,作为每周实际需求量。
令上周生产计划量与本周实际需求量做差即可得到库存值与缺货值,假设库存值为Q,.上周生产计划件数为E,上周库存量为F,本周实际需求量为T,则库存值公式如下:
由公式分析可知库存值与实际需求量[5]将影响下周结果,故将库存量作为限制条件一。
将服务水平[6]作为目标函数,假设服务水平为R,缺失值为N,实际需求量为T,则平均服务水平如下:
由题目可知,平均服务水平为101周- 177 周各服务水平的平均值,根据要求,令平均服务水平[7]大于等于85%为限制条件二。
利用bp神经网络模型,通过Matlab软件编写代码,令每周生产计划为自变量,对问题一的各物料预测量结果[8]进行处理,以呒需求周预测量为0作标准,补全177条数据作为实际需求量带入并进行6次迭代计算[9],得到各物料生产计划量,进而得出库存量、缺货量及每种物料各周服务水平。
2.2实验结果及分析
导出6种物料第101 ~ 177 周平均值的综合结果,如下表2所示:
观察表2可知,各物料的平均服务水平皆大于85%,符合题目要求。
参考文献:
[1]韩中庚.数学建模方法及其应用[M].北京,高等教育出版社,2017 年.
[2]司守奎、孙玺菁.数学建模算法与应用[M].北京,国防工业出版社,2011 年.
[3]吴孟达,成礼智.数学建模的理论与实践[M].长沙,国防科技大学出版社,1999年.
论文来源:2022年“高教社杯”全国大学生数学建模竞赛.




 < a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/dd3d/dd3d202302/dd3d2023022644-3-l.jpg">
< a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/dd3d/dd3d202302/dd3d2023022644-3-l.jpg">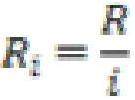 < a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/dd3d/dd3d202302/dd3d2023022644-4-l.jpg">
< a rel="example_group" title="Custom title" href="http://img.resource.qikan.cn/qkimages/dd3d/dd3d202302/dd3d2023022644-4-l.jpg">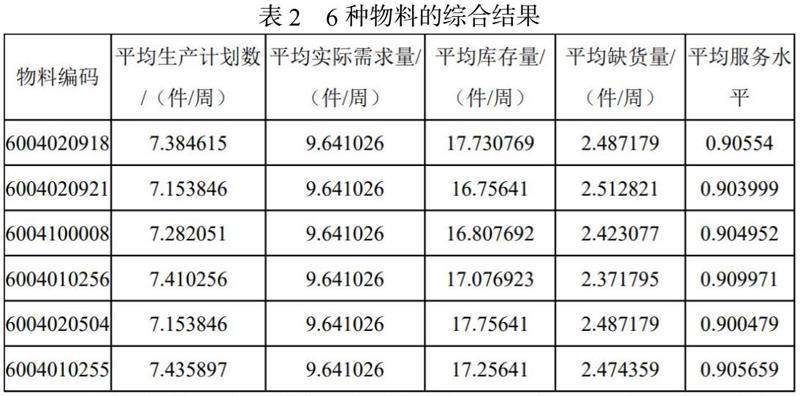

 京公网安备 11011302003690号
京公网安备 11011302003690号

