
- 收藏
- 加入书签
基于ARIMA-GM模型的中国碳交易市场价格预测研究
作者简介:林丹益(1987.8),男,汉族,浙江象山人,助理研究员硕士研究生研究方向 :低碳经济。
作者简介:彭绪山(1966.7),男,汉族,湖北恩施人,
工作单位:宁波财经学院,教授 ,硕士,研究方向 :数据挖掘。
基金项目:浙江省统计科学研究课题(项目编号:21TJQN14)
摘要:本文以2017年7月到2021年3月间广东省碳交易市场的每日碳交易平均价格为研究对象,分别运用GM(1,1)模型、ARIMA模型以及两者组合模型对碳价格进行了预测。结果表明:组合模型的预测结果更加逼近真实数据,预测精度较单一预测模型的结果更准确。
关键词:碳排放交易权价格;时间序列模型;灰色模型;Eviews
0引言
目前,我国已开通北京、天津、广东、上海、深圳、重庆、湖北和福建8大碳交易市场。但是我国碳市场处于发展初期,存在着碳市场交易不活跃、碳价低迷、以现货交易为主、金融化程度不高等问题。因此,研究碳排放交易价格并寻找其波动的客观规律可鼓励更多企业进行碳排放交易。基于此,本文选取广东省碳排放交易价格进行研究,对碳排放价格进行预测,找寻碳价格波动的客观规律。
1 灰色时间序列组合预测模型
1.1 GM(1,1)模型
灰色预测是一种对具有不确定因素的系统进行预测的方法,能有效解决数据少、序列的完整性及可靠性低的问题。GM(1,1) 模型是一种较为常用的灰色模型,GM(1,1) 预测模型的建立实质上就是对原始数据序列作一次累加生成,使生成数据序列呈显出一定规律,然后通过建立微分方程模型,求得拟合曲线,进而对系统进行预测。
1.2 ARIMA模型
ARIMA模型(自回归积分滑动平均模型)是一种根据系统观察得到的初始时间序列数据,通过曲线拟合和参数估计建立数学模型的理论和方法。ARIMA模型认为依照时间顺序进行排列的所有观测值之间都具有自相关性,这种自相关性延续了变量的发展趋势。若将这种自相关性用定量的方法描述,就可以依据时间序列的过去值预测其将来值。
1.3组合预测模型
灰色模型是通过对原始数据加工处理来弱化随机性的,若数据存在较大的波动性,预测出来的结果可能会存在较大误差。ARIMA模型对于预测的模型比较理想,要求时序数据是稳定的,或者是进行差分后是稳定的,往往需要对数据进行预处理,导致预测的精度不够准确。单一的预测模型均存在一定的局限性,很难把握预测结果的准确性,从而使得误差较大。组合模型可以通过对各个预测模型加权平均,把单一预测模型的优点集合起来,形成预测精度更高的预测模型,可以大大减小误差,使得结果更加准确。
2 实证分析
2.1数据来源及描述性统计
本文所使用的数据区间是2017年7月17日至2021年3月11日,数据截止到广东省碳排放配额(GDEA)交易的近期收盘价,其中剔除了部分零交易量的数据,数据来源于中国碳排放交易网,共计795个样本。广东省碳排放配额的市场价格并不稳定,一直处于波动状态,但总体上呈现出震荡上行的趋势,但在部分阶段会出现剧烈震荡。其中涨幅最大的一次是由2018年10月20日的9.8元/t 一直涨至2021年3月9日的35.5元/t,持续跌幅达到262.64%。
2.2时间序列预测模型
2.2.1单位根检验
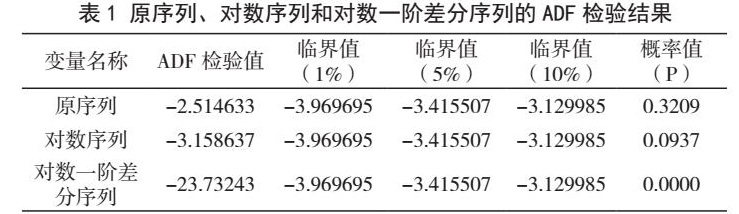
ARIMA模型要求序列是平稳序列,因此要对数据进行平稳性分析。对样本数据进行ADF检验,发现原始序列和对原序列取对数后的序列的P值分别为0.3209和0.0937,均大于5%,为非平稳序列。而对取对数后的序列进行一阶差分后的P值<5% ,在5%的显著性水平下是平稳序列。碳交易价格序列经对数一阶差分后的自相关图 ACF 和偏自相关图PACF,表1所示。
2.2.2 白噪声检验和模型定阶
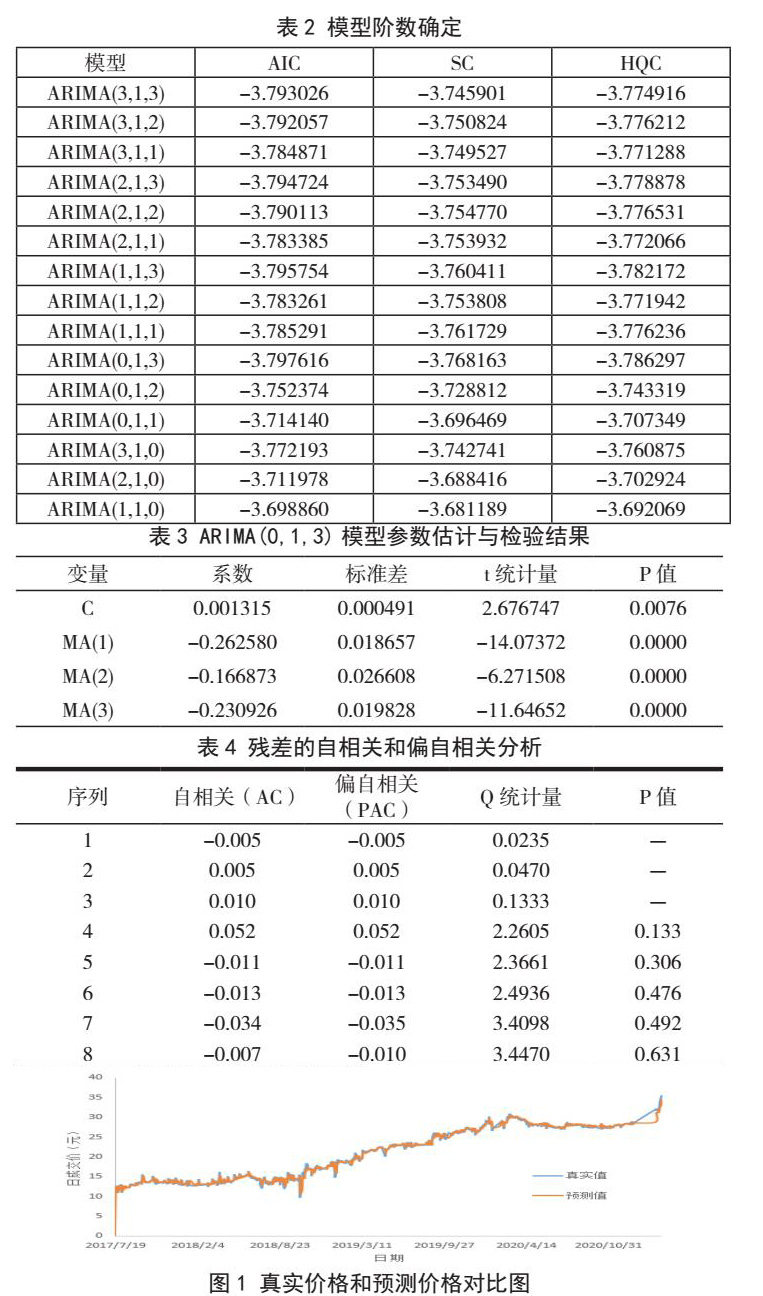
ARMA模型的p和q值确定需要观察序列的自相关和偏自相关尾部特征,同时还要确保序列不是白噪声序列,即存在有效信息。结果显示,自相关和偏自相关的Q统计量在1%的置信水平上拒绝原假设,说明对数一阶差分序列为非白噪声序列。表2是符合基本要求的15个模型检验结果对比表,结果显示ARIMA(0,1,3)的AIC值、SC值和HQC均为最低,这说明对于对数一阶差分序列建立ARIMA(0,1,3)更为合适。
2.2.3模型建立和残差检验
ARIMA模型的类型确定好之后,需要对模型参数、整个模型和残差进行检验。表3结果显示:常数项C和系数都通过了1%的显著性水平,以上检验结果均表示模型具有比较良好的统计意义。模型表达式如下:
表4为残差的自相关和偏自相关结果,可以看出,Q统计量的P值均大于 5%,即接受原假设,残差为白噪声序列,这说明原序列中的有效信息已经被提取,模型拟合效果较好。
2.2.4模型预测
利用建立好的ARIMA(0,1,3) 对广东省碳排放配额(GDEA)的日收盘价进行预测。预测结果比较如图1所示。可以看出,预测值点基本与实际值重合,说明模型预测精度较好。
2.3 GM(1,1)预测模型
按照GM(1,1)的模型求解思路,建立传统GM(1,1)模型,如下式所示。
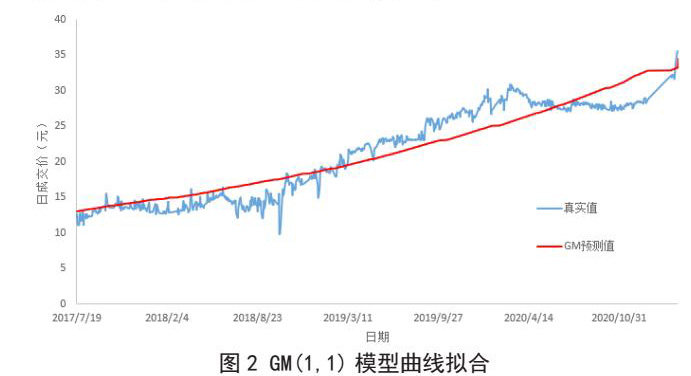
利用Matlab软件求解GM(1,1)模型,将广东碳市场日成交价作为训练数据,预测值与真实值的曲线拟合结果如图2所示。
一般情况,如果绝对误差百分比 MAPE ≤10% ,同时远点误差小于 2% 时可以认定研究结果满足精度的要求。由模型拟合结果可得:MAPE=0.8932<0.1,认为模型精度误差满足要求。后验差比值C= 0.1267 <0.35,小误差概率p=0.996>0.95,认为精度检验合格。综上可知,本次GM(1,1)灰色预测模型精度检验合格。
2.3组合预测模型
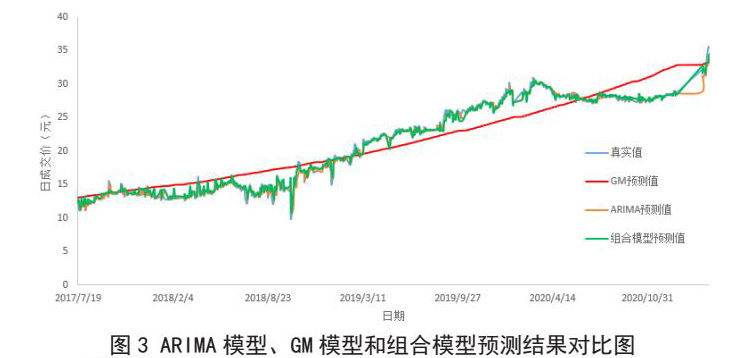
对于上述两种单一预测模型的预测精度不高、数据波动较大等问题,若结合以上两种单一预测模型的特征,构建组合预测模型。在组合预测方法中,求解方法的权系数有很多,有的从线性规划的角度出发,有的从非线性规划的角度出发,有的从正定矩阵的角度出发等方法,本文采用取方差倒数的方法求解权系数的大小,它主要思想是为了使组合预测模型的误差平方和尽可能地小,对误差平方和较小的模型赋予较高的权系数,而对误差平方和较大的模型赋予较小的权系数。根据前面ARIMA和GM模型预测结果,得到组合模型广东碳市场价格预测值,ARIMA模型、GM模型和组合模型的预测结果对比如图3所示。
3结论
单独采用灰色理论模型和时间序列模型进行预测时,由于各个单一预测模型自身条件的限制,不能全面准确地掌握原始数据的信息,影响预测结果的准确性。而通过加权组合方式对两个单一预测模型进行组合,获到的组合预测模型弥补了两种单一预测模型自身的不足。本文基于灰色GM(1,1)模型与时间序列ARIMA模型,通过加权组合方式将两种单一模型很好地融合在一起,并选取广东省碳排放权交易市场的日成交价位研究对象,对碳价格进行了预测。结果表明组合模型预测的精度和稳定性高于单项预测模型。因此,这种组合预测模型用于碳价格预测时有效可行的。





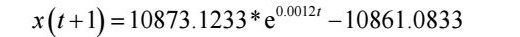

 京公网安备 11011302003690号
京公网安备 11011302003690号


