打开文本图片集

摘要：在高等教育机构中，概率论与数理统计被视为大多数专业的核心课程。这门课程的知识结构中包含了众多的抽象概念，而对于这些概念的深层含义和广泛范围，教师可能会觉得困难，而学生可能也难以完全理解。本文将Python编程应用于概率论教学。

关键词：概率论；Python；赋能；生日悖论；专业认证

本项研究利用Python进行编程，并结合特定的知识点，利用Python作为一个模型来解释概率论知识的深层含义，即通过计算模型来学习概率论知识；利用计算作为手段来处理概率论的难题，从而找到概率论的答案；以计算为载体进行概率教学实践。

一、概率论遇上Python

由于概率论和数理统计这两门课程本身具有很强的理论性和客观性，学生通常只能被动地吸收知识，并满足于能够做题，这使得学习过程具有一定程度的盲目性。这种学习方式不利于培养学生独立思考、分析和解决问题的能力。在概率论的教学过程中，一个显著的矛盾是过分强调定理的证明，因为通常会出现满屏的数学公式，这使得处理大数据量的问题变得困难，而概率论则专注于揭示大数据样本下的内在规律。

二、教学案例设计

1.问题引出。在《红楼梦》的第62回里，有这样一段描述：“宝玉的生日已经到来，没想到宝琴也正好在这一天，两人的生日是一样的。”后来我才得知，平儿和邢岫烟的生日竟然是同一天。这到底是怎么回事？探春带着笑意说：“这真的很有趣，一年中有十二个月，每个月都有几次生日，当人数增多时真是巧合”。

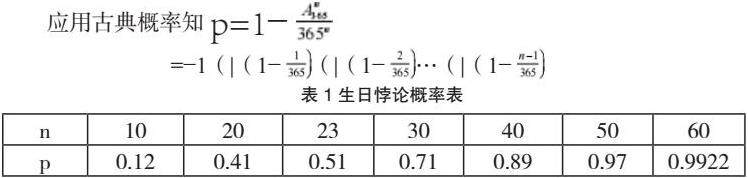
2.问题描述。所谓的生日悖论，是指在23个人中，至少有两个人的生日是相同的，这一比例超过了50%。这一问题的提出源于对一些数学现象和实际问题的思考，但它却被许多数学家认为不成立，甚至遭到反对。在一个由30名学生组成的班级里，有70%的几率会出现两名学生生日相同的情况。

这个现象描述成数学问题如下：

n（2≤n≤365）个人中至少有两个人生日相同的概率是多少？

3.问题验证

（1）验证目的。通过这种反直觉的现象，可以引导学生真正理解“随机性”，具体可以分为以下几个层次：1）基本感知：在尝试生日样本n由小变大的过程中，考察生日相同的情况，形成感官认识；2）在进行理论验证时，设计了一个等效的实验。3）在能力扩展方面：引入了真实的大数据样本，这意味着当n达到足够大的值时，生日数据大致遵循均匀分布，可以采用假设检验方法来验证分布的种类，从而增强学生的自主学习能力。

（2）验证思路。S1：随机产生了n个出生日期的样本；再根据不同月份的数据，分析得出在不同年份中出现不同生日时所需样本数。S2：研究在不同样本量n条件下的生日模式，也就是逐步增加样本量n，观察生日是否一致；S3：在固定样本量n的情况下，重复N次，并记录相同的出生次数，然后与通过公式计算得出的概率进行比较。

（3）验证步骤

1）生成样本。创建生日样本生成函数creat_birthday（n）的功能能够生成n个生日数据，并返回一个类似于[Apr-10 Mar-13]的birthday_n列表。需要注意的是，这里并没有涉及闰年的相关情况。具体代码如下：

2）探索n个样本中生日情况。定义了一个名为same_birthday（birthday_n）的函数，该函数的主要功能是对n个birthday进行计数，并确定它们是否重复。如果count>1意味着数据重复，那么就不会有相同的生日记录。具体代码如下：

有了以上的结果，学生即可形成直观的认识，可重复执行程序，加深印象增强对理论的理解。

3）重复100次求概率

S1：首先，需要对上述的same_birthday（birthday_n）函数进行简化，使其变为same_or_not（birthday_n），这样它只能判断n个样本中是否存在相同的样本。如果存在返回True的情况，那么False的关键代码将与same_birthday（birthday_n）的定义保持一致。具体代码如下：

S2：对每一个固定的n，进行100轮实验，记录100轮中出现相同生日的次数，以该次数为依据计算概率，具体代码如下：

解释：这里所说的100轮实际上等同于100个班级的数量，而n代表每个班级的人数，也就是考察100个班级中容量为10的班级的情况；若将这一问题转化成一个线性规划模型，则可以用单纯形法求出最优解。有100个班级，每个班级的容量是20个；

4）实验结论。随机性是导致人们对自己直觉产生疑虑的关键因素。在分析生日相关问题时，如果参与人数较少，随机性就会增强，从而产生一种难以言喻的缘分感觉。同时还可帮助学生了解到不同年龄人群中生日差异存在显着性。上述的实验结论是基于学生的综合总结得出的。

结语：

综合来看，Python为概率论和数理统计教学提供了强大的支持，成功地将信息技术整合到数学基础课程中，从而构建了一个“专业”与“基础”相辅相成、相互促进的健康生态环境。通过构建基于互联网平台的概率论与数理统计课堂和课后在线测试系统，使教师及时掌握课堂教学质量情况，并根据反馈意见不断改进教学方式方法，从而进一步提高教学质量。河北农业大学信息学院的18级大数据专业已经采纳了这种教学方法，并得到了学生的积极反馈，他们相信在未来会有更多的实例来支持这一教学过程。

参考文献

[1]张华兵，杨玉锋.基于概率论的油气管道风险评价方法研究[J].工业安全与环保，2024，50（01）：77-79.

[2]杨燕，程国.概率论与数理统计课程多角度思政元素挖掘——以贝叶斯公式教学为例[J].甘肃教育研究，2023，（12）：130-133.

[3]汉巍.数学建模思想在概率论与数理统计课程教学改革中的应用[J].兰州工业学院学报，2023，30（06）：156-159.