
- 收藏
- 加入书签
蔬菜类商品动态定价与补货决策研究
摘要:随着生鲜市场规模的持续扩大,蔬菜零售行业的竞争也愈发激烈。制定合理的蔬菜类商品动态定价与补货决策,提高商超收益尤为重要。本文根据一批蔬菜商品的销售数据和需求情况,对蔬菜类商品的动态定价及补货决策进行研究。利用Spearman相关系数判断各品类销量之间的相关性,然后将蔬菜单品的总销售量、每日最大销售量和日均销售量作为指标,使用K-means++聚类算法进行分类,将单品蔬菜分为:热销蔬菜、平销蔬菜、滞销蔬菜。接着建立RNN-BiLSTM组合模型各蔬菜品类总销量和进价进行预测,再根据预测结果确立决策变量,以利润最大化为目标函数,以蔬菜的定价为约束条件建立优化模型,引入模拟退火算法求出最优的补货总量和定价策略,得到最优收益方案。由此可以更加合理和精准的制定补货和定价策略。
关键字:相关性分析 K-means++聚类 RNN-BiLSTM组合模型 模拟退火
一、引言
随着社会经济的飞速发展和人民生活水平的提高,我国消费市场呈现持续活跃和稳健增长的姿态。而生鲜产品作为保障民生以及维护社会安稳的刚需性消费品,市场规模巨大。
其中生鲜产品中的蔬菜类产品具有强周期性、季节性、且易腐的自然属性,加之蔬菜品种众多且由产地不同所导致的购入成本各异,因此合理的定价和补货决策对于商家实现成本较低、利润最大化的经营目标至关重要。顾客在采购蔬菜水果这类产品时,通常产品的新鲜程度、形貌保存完好度,会成为决定其心理采购价位的主要影响因素。因此可通过较为科学系统的数学方法对蔬菜市场进行研究分析,指定动态灵活的蔬菜商品定价以及补进策略,并依据分析结果策划合理营销方案,持续换发商业活力,带来更高利润。现有一批蔬菜商品销售数据,本文根据此数据研究分析。
二、蔬菜各品类相关性分析的研究
2.1数据预处理
对这批数据进行数据预处理,便于接下来的分析与建模,首先将附件中的数据进行自然连接,对变量进行分类。为了提高数据的准确性和可靠性,按照原则剔除25803条销售数据。
观测蔬菜的销售量数据发现,部分蔬菜存在供应天数极少。此类蔬菜本文中认为是某时间段内突然出现的特殊品类蔬菜,存在供应链不稳定,或者市场需求量不稳定,购买人群较为特殊等情况,此类蔬菜本文不予进行考虑,即剔除累计销售天数不足10天的55种蔬菜单品。
2.2利用Spearman相关系数判断各品类销量之间的相关性
斯皮尔曼相关系数(Spearman)是评价2个统计变量相关性的一种数学方法,表示为:
为了便于性分析的准确性,我们挑选出蔬菜品类商品中的“花菜类”,“花叶类”,“辣椒类”,“水生根茎类”,“食用菌”,“茄类”,六大类作为特征指标进行相关性分析。
根据题目需求,设:为六大类相关性序列,为挑选出的多项指标的特征值序列;为六大类相关性序列平均值,为多项指标特征值序列平均值。
利用Python将多项指标两两之间进行Spearman相关性分析,得到蔬菜品类销售量的Spearman相关系数,可知:
I. 花叶类与其他品类的相关系数呈现较高的正相关系数。其中花叶类与花菜类的Spearman相关系数高达0.63,呈现强相关性。
II. 花菜类与其他品类的相关系数较高,表明它们之间存在较强的正相关关系。
III.辣椒类与其他品类之间的相关系数具有较强的正相关性。
IV.茄类与其他蔬菜品类之间的相关系数较低,说明茄类与其他品类之间销售量关系较弱。这与其本身的蔬菜特征有关,与实际销售规律较为吻合。
2.3使用K-means++聚类算法分析蔬菜单品关联关系
2.3.1K-means++算法步骤
K-means++算法是对传统K-means算法的拓展,抛弃了传统算法在初始聚类中心选择上随机初始化的思想。K-means++算法保证了初始化簇中心之间的相互距离尽可能远,从而避开了因为初始聚类中的随机选择而导致算法陷入的局部最优解的困境。
Step1:在数据集X中随机选择一个样本点作为第一个初始聚类中心;
Step2:筛选出其余的聚类中心:
计算样本中每一个样本点与已经初始化的聚类中心之间的距离,并记录最短距离;
计算每个样本点被选为一下聚类中心的概率,并将最大概率值对应的样本点作为下一个簇中心;
Step3:重复以上步骤,确定K个聚类中心;
2.3.2蔬菜单品聚类中心
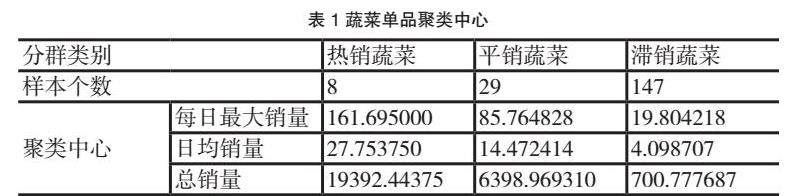
将单品的总销售量、每日最大销售量和日均销售量作为指标,使用聚类算法进行分类,将单品蔬菜分为:热销蔬菜、平销蔬菜、滞销蔬菜。得到下表:
2.3.3模型求解
利用Python求解,模型轮廓系数约为:0.7669221849032795聚类效果较好。
各单品的销售量聚类结果分析:
热销类蔬菜中的单品具有高总销售量、高每日最大销售量和高日均销售量的特征。这意味着这些单品的销售非常火爆,因此为后面问题的补货决策提供一定帮助。热销类单品之间存在很高的相关性,其之间的销售指标相互影响较大。
平销类蔬菜中的单品相对于热销类的蔬菜,总销售量、每日最大销售量和日均销售量略低,但是销售指标在中上等水平。此类中的蔬菜单品之间的存在一定的相关性,但在单品之间不足以形成较大的影响。
滞销类蔬菜中的单品均表现为较低的总销售量、每日最大销售量以及日均销售量。此类中的蔬菜单品均存在较弱的相关性,之间的销售指标相互影响较小。
三、蔬菜补货与定价决策模型构建
3.1基于RNN-BiLSTM模型的蔬菜预测模型
3.1.1RNN-BiLSTM模型
循环神经网络(Recurrent Neural Network,RNN),是一种在预测序列数据问题上有着良好表现的神经网络模型。当其处理输入的序列信息时,将信息放置于内部的隐藏层(Hidden layer)中,可以将隐藏层看作为网络的记忆,能对所有先前时间步骤中发生的事件信息进行捕捉。
循环神经网络(RNN)的缺陷:RNN会受到短时间记忆的影响,当一条数据足够长的时候,信息传递时间的增长会影响信息传递速率,进而导致RNN遗忘先接收的长序列中的元素,使得信息失真率上升。所以RNN只能利用其短时间记忆的能力去传递较短的数据。
双向长短期记忆网络(Bidirectional Long Short-Term Memory),简称BiLSTM,是对长短期记忆网络(LSTM)[1]的一种拓展,具有两个方向的结构,分别处理正向和反向的输出序列,能够保证网络同时对过去和未来的信息进行分析。BiLSTM通过这种双向结构,可以更全面地捕捉序列数据中心的上下文信息,有助于解决梯度消失的问题,利于更好地捕捉长期依赖。
RNN-BiLSTM模型综合利用RNN和BiLSTM的优势,提高了对长期依赖关系的建模能力,并且让模型能够在考虑整个序列上下文的任务中更全面地捕捉上下文的信息,有助于提高任务性能。
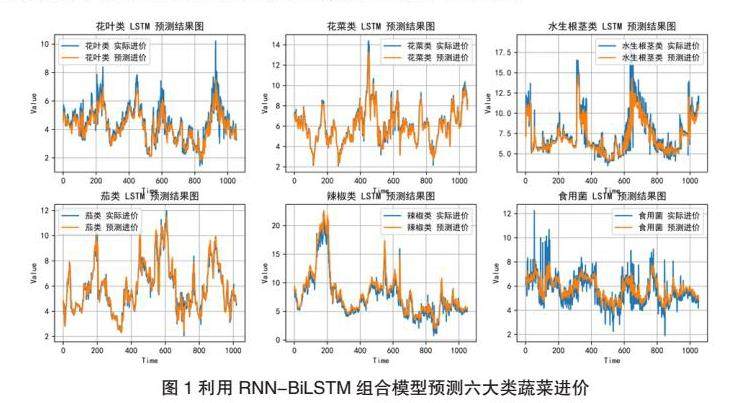
在本文中,我们利用Python搭建RNN-BiLSTM模型对进价及销售量进行预测,六大类蔬菜品类进价的预测结果如下图所示:
通过R方、MSE、RMSE以及MAE这些指标对组合模型预测六大类蔬菜进价的预测结果进行检测,主要模型参考指标R方多大于0.7,更有过半的数据超过0.91接近于1,同时MSE、RMSE以及MAE效果很好。因此本文认为该组合模型对六大蔬菜品类的进价预测效果理想。
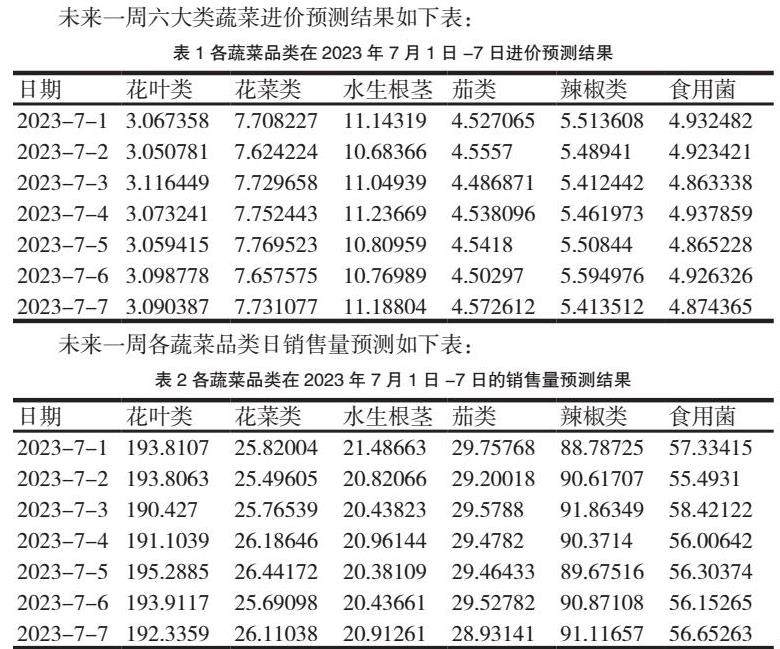
未来一周六大类蔬菜进价预测结果如下表:
未来一周各蔬菜品类日销售量预测如下表:
3.2最大化利润的优化模型求解
3.2.1建立优化模型
(1)目标函数的建立
由于蔬菜类商品为易逝品,存放时间过长会导致蔬菜的新鲜程度大幅降低,严重顾客的购买体验。因此不同品类蔬菜的补货量应该与自身当日的预测销售量 所持平,从而减少商超的损失。同时为了商超利润的最大化,将补货途中导致破损的蔬菜进行打折销售,从而减少了因为破损而完全损失的蔬菜价值,于是得到以下目标函数:
其中Pij、Bij、Li、Sij、k 分别表示第i类蔬菜第j天的定价、批发价格、商品平均损耗率、日销售总量、破损蔬菜打折力度系数。
(2) 约束条件的建立
因为将各品类日补货量替代为各品类当日的预测销售量,所以只需要对商品定价进行约束。鉴于商超的利润策略,每种蔬菜品类的定价被确立为维持在其单位成本的110%至160%之间。这个定价策略旨在保障利润,同时避免定价过高影响产品销售。
(3) 优化模型整体呈现
3.2.2基于模拟退火算法求解优化模型
(1)算法原理
模拟退火算法的基本思想是从某一较高初始温度出发,伴随温度参数的不断下降,结合一定的概率突跳特性在解空间中随机寻找目标函数的全局最优解。即在局部最优解中有概率性的跳出并且趋近于全局最优解[2]。
(2)模拟退火优化模型步骤
Step1:给定初始温度T = 1.0,温度衰减系数,再随机产生初始状态。
Step2:每个温度迭代最多不超过100次。
Step3:最小温度为。
Step4:直到算法终止准则满足:输出算法搜索结果
(3)模型求解
根据优化模型求解得到未来一周最大收益为8019.608878650019元。
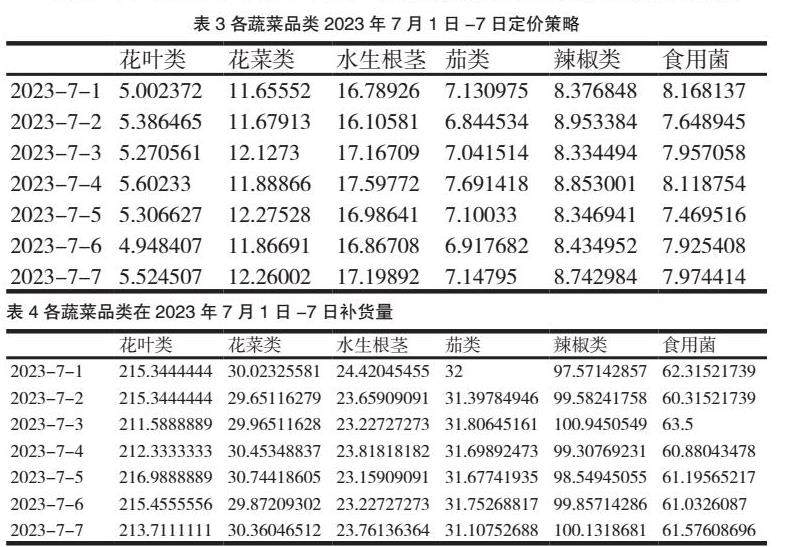
未来一周(2023年7月1-7日)各品类蔬菜的每日补货量和定价策略。
四、模型推广
在上述模型建立与求解的基础上,可以进一步推广该模型的应用范围。首先,可以考虑将该模型应用于其他类型的商品销售分析,例如水果、肉类等。通过对不同类型商品的销售数据进行类似的分析和处理,可以发现各类商品销售量的分布规律和相互关系,为商超的经营决策提供有力的支持。其次,可以通过扩展模型假设来增加模型的适用性。例如,我们可以考虑引入其他影响因素,如天气、节假日、促销活动等,对销售数据进行分析和处理。这样可以更准确地预测未来销售趋势,并制定更有效的销售策略。
参考文献
[1]崔云浩.基于CNN-PSO-LSTM组合模型的生鲜蔬菜销量预测研究[D].安徽农业大学,2022(02).
[2] 刘相锦,马跃.基于模拟退火算法优化的BP神经网络期权定价研究[C].第十八届(2023)中国管理学年会暨“一带一路”十周年研讨会论文集,2023.





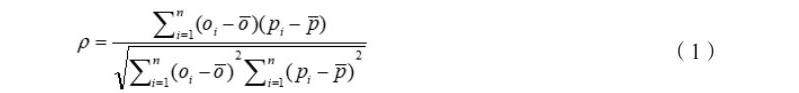

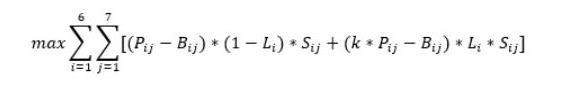


 京公网安备 11011302003690号
京公网安备 11011302003690号


