摘要：在初中数学教学中，课堂问题设计是引导学生思考、促进知识掌握和能力提升的关键环节。逻辑思维作为数学学科核心素养的重要组成部分，其发展具有明显的层级性。基于逻辑思维层级设计具有梯度的课堂问题，能够更好地契合学生的认知发展规律，激发学生的学习兴趣，提高课堂教学效率。本文旨在探究基于逻辑思维层级的初中数学课堂问题梯度设计策略，为初中数学教学实践提供参考。

关键词：逻辑思维层级；初中数学；课堂问题

逻辑思维层级为初中数学课堂问题梯度设计提供了理论依据。不同的逻辑思维层级对应着不同难度和类型的问题，基于逻辑思维层级设计问题梯度，能够使问题更加符合学生的思维发展过程，让学生在解决问题的过程中逐步提升逻辑思维能力。同时，合理的问题梯度设计也能够促进学生逻辑思维层级的不断提高，形成良性循环。

一、基于逻辑思维层级的初中数学课堂问题梯度设计存在的问题

（一）问题梯度缺乏逻辑性

部分教师设计的课堂问题未遵循逻辑思维层级的递进规律，问题间缺乏内在逻辑关联。在思维层级转换上，常出现跨度不合理的情况，或突然跳跃至较远层级，使学生思维衔接断裂；或在同一层级重复设问，难以推动思维向纵深发展。这种缺乏逻辑性的梯度设计，导致学生无法形成系统的思维链条，阻碍了逻辑思维的有序发展，也降低了问题对学生思维的引导效能。

（二）问题设计与学生实际思维水平不匹配

一些教师对学生现有逻辑思维水平缺乏精准把握，导致问题设计与学生实际能力脱节。部分问题过于浅显，无需深度思考即可解答，无法激发学生的思维活跃度和学习主动性；另一些问题则难度过高，超出学生当前思维承载范围，易使学生产生畏难情绪，削弱学习自信心。这种不匹配的设计，既难以实现教学目标，也不利于学生在适度挑战中提升逻辑思维能力。

（三）问题类型单一，忽视高阶逻辑思维的培养

当前课堂问题设计多集中于低阶逻辑思维层级，以考查基础知识的记忆、理解为主，问题类型较为固化。对于归纳与演绎、综合与创新等高阶逻辑思维层级的问题涉及较少，未能为学生提供足够的高阶思维训练机会。这种单一化的问题类型，限制了学生逻辑思维的全面发展，不利于培养学生运用数学思维解决复杂问题的能力，与数学核心素养的培养要求存在差距。

二、基于逻辑思维层级的初中数学课堂问题梯度设计策略

（一）依据逻辑思维层级，构建递进式问题链

逻辑思维层级由低到高包含感知与识别、分析与比较、归纳与演绎、综合与创新等。构建递进式问题链，需遵循层级递进规律，以低阶思维问题为基础，逐步向高阶拓展，让学生思维随问题推进持续攀升。通过问题间的逻辑衔接，引导学生主动思考，系统构建知识关联，深度理解数学知识本质，逐步提升逻辑思维的系统性与连贯性。

以“第十五章二次根式”中“15.1 二次根式”教学为例。教师可依逻辑思

2 3维层级构建问题链：在感知与识别层级，设计问题“观察 这类式子，从形式上看有什么共同特点？”引导学生识别二次根式的外观特征；进入分析与比较层级，提问“对比二次根式与已学的整式、分式，在表达式结构和取值范围上有哪些不同？”促使学生剖析二次根式独特性；到归纳与演绎层级，设置问题“结合前面例子，归纳二次根式的定义，再判断 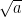（a满足什么条件时）是二次根式？”让学生先归纳规律再演绎应用；进入综合与创新层级，抛出问题“请根据二次根式的定义，自编几个二次根式的例子，并说明设计思路，还可尝试改变条件构造非二次根式式子对比”，推动学生综合运用知识并创新思考，借这样的问题链，逐步提升学生逻辑思维。

（二）结合学生实际思维水平，设计分层问题

学生逻辑思维水平存在个体差异，分层问题设计需精准把握学情。依据学生现有思维能力，将问题分为基础、提升、拓展层。基础层问题面向逻辑思维起步阶段学生，巩固知识；提升层适配中等水平学生，深化理解；拓展层针对高阶思维学生，激发潜能。通过分层，让各层次学生都能在适配问题中获得思维锻炼，增强学习信心与动力，逐步提升逻辑思维。

以“第十三章全等三角形”中“13.3 全等三角形的判定”教学为例。教师先了解学生情况，再分层设计问题。基础层，面向思维基础弱的学生，设计“全等三角形有哪些基本判定方法（SSS、SAS等），分别是什么含义？”帮助学生牢记判定方法；提升层，针对中等水平学生，提问“已知两个三角形有两组边和一组角，怎么判断这组角的位置，才能用SAS或SSA（SSA不能判定全等，借此辨析）判定，说说理由”，引导学生深入分析判定条件差异；拓展层，给思维能力强的学生，设置“现有一个破损的三角形玻璃，要配完全一样的，至少带几块碎片，依据哪个判定方法，尝试多种情况分析”，让学生综合运用判定知识解决实际问题，不同层次问题适配学生思维，助力提升逻辑思维。

（三）丰富问题类型，注重高阶逻辑思维的培养

高阶逻辑思维（归纳与演绎、综合与创新等）对学生数学素养提升至关重要。丰富问题类型，需增加开放性、探究性、综合性问题占比。开放性问题拓宽思维广度，探究性问题挖掘思维深度，综合性问题提升知识整合与应用能力。通过多样问题，促使学生突破低阶思维局限，主动运用高阶思维分析、解决数学问题，培养创新与综合思维能力。

以“第十六章轴对称和中心对称”中“16.1 轴对称”教学为例。教师设计多样问题培养高阶思维。开放性问题：“生活中还有哪些轴对称的例子，它们的对称轴有什么特点，尝试分类列举”，让学生从生活中挖掘素材，自主分类归纳；探究性问题：“探究一个图形是轴对称图形的前提下，增加什么条件能让它的对称轴数量变化，以等腰三角形和等边三角形（等腰三角形一般1 条对称轴，等边三角形3 条）为例分析”，引导学生深入探究图形与对称轴关系；综合性问题：“结合轴对称知识，设计一个轴对称图案用于班级文化展示，说明设计理念，还要考虑图案中各部分的对称关系及实际应用效果”，促使学生综合运用知识创新设计。借这些问题，推动学生高阶逻辑思维发展，提升数学应用与创新能力。

三、结语

综上所述，基于逻辑思维层级的初中数学课堂问题梯度设计存在问题梯度缺乏逻辑性、与学生实际思维水平不匹配、问题类型单一等问题。解决这些问题，需教师把握逻辑思维层级规律，结合学生实际设计问题。这不仅能提升课堂教学质量，更能系统培养学生逻辑思维能力，为其数学核心素养发展奠定基础，值得教育工作者持续探索与实践。

参考文献

[1]刘国庆.探索问题导学法在初中数学教学中的应用[J].课堂内外（高中版）,2024(2):35-37.

[2]费佳璇.问题驱动式教学在初中数学课堂中的应用研究[D].湖南工业大学,2023.