摘要：三年级学生初学小数，尤其在简单计算中，暴露出诸多源于概念理解不清、整数负迁移及数感薄弱等方面的错误。本文基于教学实践，通过深入剖析错误背后的深层原因，从概念表象、强化算理、联系生活实际应用三个维度，提出了相应的教学改进策略，旨在帮助学生筑牢小数学习的根基，实现从整数到小数知识的顺利过渡与正迁移。关键词：小数初步认识；计算错误；案例分析；教学策略；三年级数学

《义务教育数学课程标准（2022 年版）》在小学阶段的“数与代数”领域明确指出：结合具体情境，初步认识小数，能进行小数的加减运算。本文聚焦三年级学生在小数简单计算中出现的典型案例，进行深入归因分析，并在此基础上探索行之有效的教学策略，旨在为一线教师提供有针对性的教学参考，帮助学生在小数学习的起始阶段“扣好第一粒扣子”。

一、小数计算错误的典型案例分析

通过对学生课堂练习及课后作业的持续观察与记录，将常见的错误归纳为以下三种典型类型。

(⟶) 案例一：数位概念混淆型错误——以 ^ω12.8+5^′′ 为例错误表现：在计算 ^ω12.8+5^′′ 时，部分学生给出的答案是“17.8”或“12.13”。

错误解法1： 12.8+5=17.8 （将5 与8 相加）

错误解法2： 12.8+5=12.13 （将5 视为0.5，与8 相加后进位）

错误成因分析：

1.小数数位概念模糊：这是最核心的原因。学生虽然会读“十二点八”，但并未真正理解“8”在十分位，表示8 个0.1，而“5”在个位，表示5 个1。学生潜意识里仍将“12.8”看作一个整体“128”或“十二和八”，导致在竖式计算时，无法实现真正的“相同数位对齐”。

2.“小数点对齐”法则的理解形式化：学生记住了“小数点对齐”这一规则，但并未理解其本质是确保“相同数位对齐”。当加数 ⁴5^′′ 没有明显的小数点时，学生便不知所措，要么将5 的末位与8 对齐（错误1），要么凭空给5 添加小数点后再对齐（错误 2）。

3.位值制理解不贯通：整数的位值制（个、十、百……）概念牢固，但对小数部分新的位值制（十分位、百分位……）未能实现同化与顺应，无法将整数与小数部分作为一个统一的十进制系统来理解。

（二）案例二：整数计算规则负迁移型错误——以 ^ω1.2⋅0.8^γ 为例

错误表现：在计算“1.2 - 0.8”时，部分学生模仿整数减法中“大数减小数”的规则，得出“0.6”的错误答案。即：2 - 8 不够减，用 8-2=6 ，结果是0.6。

错误成因分析：

1.整数计算经验的强势负迁移：在整数减法中，当被减数的某一位小于减数的对应位时，学生已熟练掌握“借一当十”后再减的方法。但在小数情境下，面对“2-8 不够减”的类似情境，部分学生采取了“走捷径”的策略，直接套用“大数减小数”这一在整数比较中成立的规则，而忽略了减法的根本意义。

2.对小数的数值大小缺乏直观感知：学生未能通过元角分模型（1.2 元是1 元2 角，0.8 元是8 角）或长度模型（1.2 米是1 米2 分米，0.8 米是8 分米）来直观判断结果应比 1.2‰ ，从而未能对计算结果进行有效估算和检验。

3.算法程序掌握不牢：学生可能没有真正掌握小数部分不够减时，需要从整数部分“借1 当10”的算理。这与整数减法的算理一脉相承，但学生未能实现知识的正向迁移。

（三）案例三：生活经验缺失型错误——以 ^ω1.5+0.5^′′ 为例错误表现：极少数学生在口算 1.5+0.5³[ 时，会给出“1.10”或“2.0”的答案，并在写成竖式时出现数位混乱

错误成因分析：

1.“满十进一”的进制观念在小数部分应用不畅：学生知道5+5=10，但“10”在十分位上如何表示？整数部分“满十进一”的观念根深蒂固，但到了小数部分，学生不清楚十分位上“满十”后，应该向哪个方向进位（是向整数位的个位进一，还是向小数部分的百分位“进”？），从而产生困惑。

2.生活原型支撑不足：虽然教材引入了元角分模型，但部分学生对“1.5 元+0.5 元”即“1 元 5 角+5 角”的现实情境不熟悉，无法将抽象的算式与“5 角+5 角=1 元，再加上原来的 1 元，一共2 元”这一具体操作过程建立有效连接。当数学运算脱离了有意义的生活背景，就变成了纯粹的符号游戏，容易出错。

3.对计算结果“化简”的意识薄弱：得出 ^′′2.0^′′ 的学生，可能知道结果是2，但缺乏将 ^∗2.0^∗ 写成最简形式“2”的意识，这反映了对小数性质（小数末尾的0 可以去掉）的初步认识不足。

二、基于错误分析的教学策略探索

针对上述典型错误，教学不应止于指出错误和纠正答案，而应追本溯源，从概念建构、算理理解和应用体验等方面进行优化。

（一）策略一：多元表征，深度建构——筑牢小数的概念基础

小数的抽象性是学生理解困难的根本。教学必须充分利用多种直观模型，帮助学生实现从具体到抽象的过渡。

1.强化“元角分”与“米制”系统的桥梁作用。在课程引入和初期练习阶段，应大量使用元、角、分和米、分米、厘米等学生熟悉的单位进行换算和计算。例如，将 ^ω12.8+5^′′ 转化为“12 元8 角 +5 元”的问题，学生能自然而然地想到“元加元，角加角”，从而直观理解“相同单位才能相加减”的道理，这为“相同数位对齐”提供了坚实的生活经验支撑。

2.善用几何直观模型（如面积模型、数轴）。使用百格图，将整个正方形视为 "₁⋅ ，其中一行（十格）就是0.1，一格就是 0.01。通过涂色、拼接等方式，让学生直观看到 ^ω0.5+0.5^′′ 正好拼满一行，也就是 1。数轴则能帮助学生建立小数的顺序感和大小观念，对于判断计算结果的合理性至关重要。

3.促进不同表征方式间的转化。 设计活动，要求学生将同一小数用语言（读法）、符号（数字）、图形（模型）和情境（元角分）等多种方式表示出来，并相互转换。这种“翻译”的过程，正是学生深化对小数意义理解的过程。

（二）策略二：对比辨析，明晰算理——实现整数到小数的正迁移教学的关键在于引导学生发现新旧知识间的联系与区别，化“负迁移”为“正迁移

1.开展整数与小数计算法则的对比教学。在教授小数加减法时，可以有意识地设置与整数加减法的对比环节。例如，将“125+34”与“1.25+3.4”的竖式并列书写。引导学生讨论：它们的共同点是什么？（都是相同数位对齐；都遵循“满十进一”、“退一当十”的规则。）不同点是什么?（整数是个位对齐，小数是小数点对齐；整数的数位向右延伸，小数的数位向左延伸。）通过对比，让学生深刻理解“小数点对齐”的本质就是“相同数位对齐”，十进制计数的思想在整数和小数领域是统一的。

2.突出“十进制”思想的核心统领地位。教师要反复强调，无论是整数还是小数，其计数和计算都基于“十进制”。个位的 10 倍是十位，反之，个位的十分之一（即除以 10）就是十分位。通过这样的阐述，帮助学生将整数数位表向右扩展，构建出完整的十进制数位顺序表，打通整数与小数之间的壁垒。

3.加强估算教学，培养数感。在计算前，要求学生先估一估结果的大致范围。例如，计算“1.2 - 0.8”前，问学生“结果会比1 大还是比 1 小?”，引导学生意识到“1.2 减去一个比 1 小的数，结果肯定比 1.2 小，但比0.2 大”，从而在计算前就能对结果的合理性有一个预判，有效避免 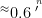这类明显不合理的答案。

结语

三年级学生的小数计算错误是其数学思维发展过程中的必然现象，是宝贵的教学资源。教师应以积极的心态看待这些错误，将其作为诊断学情、改进教学的重要契机。只有从机械训练转向概念理解，从孤立教学转向联系对比，从符号操练转向实际应用，才能真正帮助学生克服整数认知的定势干扰，深刻理解小数的本质含义和运算的算理算法。

课题：珠海市教育科研规划课题2023 年度（课题编号：2023ZHGHKT122）成果。

参考文献

[1]中华人民共和国教育部.义务教育数学课程标准（2022 年版）[S].北京：北京师范大学出版社,2022.

[2]张奠宙,孔凡哲,等.小学数学研究[M].北京：高等教育出版社,2009.