摘要：中小学数学知识是学生学习高等数学的必要基础。小学、初中、高中三个学段密切联系。在初高衔接中，教师要关注哪些初中知识点在高中会经常应用到，有意识地培养学生运用这些知识点解决问题的能力。本文通过一节初高衔接教学公开课，展示知识的生成、应用和提升，唤起学生对“一元二次方程根与系数的关系”知识点的关注和掌握，初步建立起方程与函数的关联，在初高中数学学习中架起代数思维贯通的桥梁。

关键词：初高衔接；题组训练

中小学数学知识是学生学习高等数学的必要基础。根据学生的年龄特点和认知水平，这些知识被安排在小学、初中、高中三个阶段进行螺旋式的学习。因此，初中教师在教学中不仅要落实好本阶段知识的教学，也要了解小初、初高的知识衔接。在初高衔接中，教师要关注哪些初中知识点在高中会经常应用到，有意识地培养学生运用这些知识点解决问题的能力。教学中，我重视初高衔接知识点的选取，将初中与高中的运用方法糅合，渗透到教学中，为高中的学习打好基础。笔者曾于“粤东基础教育数学学科群名师工作坊”活动中执教《一元二次方程的根与系数的关系》的初高衔接公开课，通过知识的生成、应用和提升，唤起学生对该知识点的关注和掌握，初步建立起方程与函数的关联，在初高中数学学习中架起贯通的桥梁。

一、缘于课标，始于实际需要

本节课主要研究一元二次方程的两根之和、两根之积与方程的系数之间存在的特殊关系，是对一元二次方程的根的探索的延续和应用的体现。一元二次方程根的判别式、根与系数的关系在高中数学中都有着广泛的应用，是学习高中数学的必备基础[1]。

《义务教育数学课程标准（2022 年版）》也已将“了解一元二次方程的根与系数的关系”[2]改为必学内容。于是，我将本节课作为初高数学衔接课予以探究，为初高衔接教学做出尝试，收获经验。

二、亲历探究，终在落实应用

1、温故知新，探索新知

问题一：(1)解方程： ①x²-2x-8=0 ； ②x²-6x-7=0 ； ③2x²-18=0 ； ④3x²+4x+1= 0 。(2)已知长方形的长和宽是方程 x²-3x+2=0 的两个实数根，求长方形的周长和面积。问题二：猜想一元二次方程的根与系数有何关系？并验证之。

师生活动：先让学生运用已学知识解决问题；教师再引导学生观察周长的一半、面积分别与方程的两根的关系，让学生大胆猜想并用第(1)小题中各个方程的两根与系数关系作比对，验证正确与否；最后再引导学生运用求根公式证明，从而得出一元二次方程的根与系数的关系。

教学分析：孔子曰：“温故而知新，可以为师矣。”本环节通过设置复习环节，从解方程得出方程的根、求解周长（两根和）和面积（两根积），进行有指向性的观察，让学生发现、猜想、实例及通式验证，探索出新知。从已知到未知，是数学探索的常见方式之一，也是培养学生观察能力、逻辑推理能力的有用方法。

题组训练，逐级提升

问题三：同学们，你能运用所学知识解决以下几个题组的问题吗？

题组Ⅰ：(1)已知关于 x 的方程 x²+mx-20=0 的一个根为 5，求它的另一个根。

(2)（2023•天津改编）已知 X₁,X₂ 是方程 X²-6X-7=0 的两个实数根，则 x₁+x₂=. 。

(3)若 x1、x2 是一元二次方程 x2-3x-10=0 的两个实数根，则代数式 =

题组Ⅱ：(1)已知一元二次方程 x²-4x+k=0 的两个实数根为 x₁ 、 x₂ ，若 X₁X₂ +3x₁+2x₂=1 ，则实数 k= 。(2)若关于 x 的一元二次方程 x²-9x+m-0 的两个实数根为 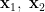，若 x₁=2x² ，则实数 m 的值为。(3)（2023•四川南充）已知关于 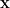的方程 x²-(2m-1)x-3m²+m=0.① 求证：无论 ρ_m 为何值，方程总有实数根； ② 若 x₁ 、x2 是方程的两个实数根，且 ， 求 m 的值。

题组Ⅲ：（1）已知抛物线 y=x²-3x+m+1 ， ① 若它与 x 轴的两个交点都在 x 轴的正半轴，求 m 的值； ② 若与 x 轴的两个交点在 y 轴的两侧，求 m 的取值范围；③ 猜想：抛物线与 x 轴的两个交点有没有可能都在 x 轴的负半轴？并说明理由。(2)已知二次函数 y=x²+4x-2m+5 的图象与 x 轴有两个交点 .D. 求实数 m 的取值范围； ② 若二次函数的图象与 x 轴的两个交点在 Δy 轴的同侧，且交点横坐标均为整数，求整数 m 的值.

师生活动：题组Ⅰ是直接应用，设定为抢答题；题组Ⅱ需要转化、计算，设计为板演和提问回答的形式；题组Ⅲ需要综合运用，安排为小组讨论，代表发言的形式。

教学分析：本环节采用题组训练的模式，从初中常见的题目方式，向高中衔接的综合类练习过渡，逐级提高运用知识的能力，培养综合应用意识，拓宽思维广度。题组Ⅲ让学生明白：根与系数关系从方程中来，但不仅仅是服务于与方程有关的题目，还与二次函数、二次不等式的应用密切相关，这就为初高中数学的学习搭起了衔接的桥梁。

总结归纳，提炼方法

问题四：本节课你收获了什么新知识？如何应用？应用中与哪些知识有关？体验了哪些思想方法？对比你的认知，有什么意外的收获吗？想一想自己还有什么困惑之处？

教学分析：有指向性的提问式总结让学生的思维不跑偏。学生总结时提到“一元二次方程根与系数的关系对于解决抛物线与 x 轴交点的位置关系竟然有很大的帮助，感到意外”；不足之处也是这方面的联系运用不太熟悉，有待加强。让学生有归纳、有反思，有利于培训他们良好的学习习惯。

三、教学反思，收获衔接经验

本节课为初高衔接探究课，遵循学生的认知规律，通过问题串、题组的方式，引导学生经历从已学向未知的探索过程和综合应用，逐步揭开一元二次方程的根与系数的关系的神秘面纱，亲身体验其应用范围之广，感受它的有用性、可用性，逐步将初中数学相对具体的知识模式向高中相对抽象的逻辑思维方式过渡，为迈进高中阶段学习做足准备。

1.找准契合点，架起初高贯通桥梁。函数是高中数学知识重要的一部分，从函数观点看一元二次方程和一元二次不等式是高中知识学生的预备部分[3]，一元二次方程的根与系数的关系是这一知识的重要一环，知识的起点在初中，将其作为衔接的契合点，自然构建初高数学知识连接的桥梁。

2.精选练习题，形成梯度循序提升。在初高衔接教学中，习题选择有很高的要求，要有针对性的寻找、筛选，甚至是改编、原创。本节课题组的设计充分体现螺旋上升，梯度性强，关联二次方程、二次函数、二次不等式知识模块，架起初高思维贯通的桥梁。

3.注重教学评，培养学科核心素养。课堂教学中，教师既注重差异化教学策略的创新，采用题组进阶，多元互动，又关注学生反馈，更重视“认知意外”和“困惑之处”的反思价值，真正体现教学评一体化。教学中重视思想方法的渗透，关注数学能力的培养，由观察猜想→逻辑验证→迁移应用→批判反思，路径清晰，有助于培养学生学科核心素养。

参考文献：

[1]孔冬青.一元二次方程的求根公式[J].中学数学教学参考（中旬） 2019（7）：26-28

[2]中华人民共和国教育部制定.义务教育数学课程标准(2022 年版)[S]. 北京:北京师范大学出版社,2022:4

[3]中华人民共和国教育部.普通高中数学课程标准（2017 年版2020 年修订）[S].北京：人民教育出版社，2020.