摘要：随着人工智能技术的快速发展，生成式 AI（如 ChatGPT、文心一言等）在教育领域的应用日益广泛。本文以高中数学“函数单调性的判定”教学为例，探 讨如何利用生成式 AI 赋能问题驱动教学（Problem-Based Learning, PBL），优化传统课堂模式。通过设计 AI 辅助的问题情境、动态生成变式训练、智能反馈学习路 径，提升学生的数学思维能力和课堂参与度。生成式 AI 能够有效支持问题驱动教学，促进学生对函数单调性概念的深度理解，并为高中数学智能化教学提供新思路。关键词：生成式 AI、问题驱动教学、函数单调性、课堂实践

函数单调性是高中数学的核心概念，其判定方法（如定义法、导数法）是后续学习极值、最值等问题的基础。传统教学中，教师通常采用“讲解—练习”模式，学生容易陷入机械记忆，难以灵活应用。问题驱动教学（PBL）通过真实情境激发学生探究，但受限于教师精力，难以实现个性化指导。

生成式 AI 具备自然语言处理、动态生成题目、智能答疑等功能，可弥补传统 PBL 的不足。本文结合教学实践，探讨如何利用生成式 AI 优化问题驱动的函数单调性课堂，提升教学效率。

一、生成式 AI 与问题驱动教学的融合模式

（一）生成式 AI 的教育应用优势

生成式人工智能（AI）在数学教育领域展现出显著的应用价值，其核心优势主要体现在三个方面。首先，在动态问题生成方面，AI 能够基于学生的实际学习水平，智能构建具有针对性的问题序列。以函数单调性教学为例，系统可以自动生成阶梯式问题：对于基础薄弱的学生，提供如"判断线性函数 f（x）=2x+1 的单调性"这类直观问题；对于能力较强的学生，则可生成含参数的变式问题，如"已知二次函数 scriptstylef（x）=ax²+bx+c 在区间 （-∞，2] 单调递减，求参数 a 的取值范围"。其次，AI 具备强大的即时反馈与解析功能，能够对学生解题过程进行实时分析，精准识别常见错误。最后，基于大数据分析的个性化学习路径规划是 AI 的另一大优势，系统通过收集学生的错题数据，智能推荐专项训练内容。

（二）问题驱动教学的设计框架

问题驱动教学（PBL）在函数单调性教学中采用三阶段框架：首先通过 AI模拟股票走势、气温变化等生活案例，直观呈现函数变化规律，引出单调性概念；其次由 AI 生成递进式问题链，从基础概念到高阶应用，循序渐进培养学生思维能力；最后组织分组探究，AI 实时分析讨论内容，在关键节点给予智能提示。这一框架将生活情境、阶梯问题和智能辅助有机结合，使抽象概念学习更加生动有效。

二、课堂实践案例：函数单调性的判定

（一）教学目标

本教学设计围绕函数单调性判定这一核心内容，确立了三维一体的教学目标体系。在知识维度，要求学生精准掌握用定义法（通过比较函数值大小）和导数法（通过分析导函数符号）判定函数单调性的具体步骤与操作规范，理解两种方法的适用条件与内在联系。在能力发展维度，重点培养运用数学语言描述变化规律的建模能力，以及通过严谨的代数推导和逻辑分析解决单调性问题的推理能力。在情感态度维度，通过AI 辅助的探究活动，激发学生对函数性质研究的求知欲，引导其体验智能技术对数学学习的赋能作用，培养数字化学习时代所需的科技素养。

（二）教学流程

环节1：AI 情境导入

在课堂导入环节，教师利用生成式 AI 的可视化功能，动态呈现多种函数图像的演变过程。AI 系统首先展示标准抛物线、指数函数和对数函数的图像，通过色彩渐变技术直观标注函数值随自变量变化的趋势区域。教师提出引导性问题："观察这些曲线的不同区段，你能识别出哪些部分呈现上升趋势？哪些部分呈现下降趋势？"随后，学生通过交互式界面实时调整函数参数，如改变一次函数f（x）τ=ax+b 中的斜率 a 值，观察函数图像倾斜角度的变化如何影响单调性特征。

环节2：问题链探究

在核心探究环节，AI 系统根据学生的认知水平智能生成递进式问题序列。首先，针对定义法的学习，AI 呈现反比例函数 f（x）=1/x ，要求学生严格按照定义证明其在 （0，+∞） 上的单调递减性。系统会智能监测学生的证明过程，当发现学生忽略"任意取 X₁，X₂∈D^′ 这一关键前提时，AI 会即时弹出提示框，引导学生思考："比较 f（x₁）-f（x₂） 与 X₁-X₂ 的符号关系时，是否需要考虑 x₁ 和 x₂ 的任意性？"接着转入导数法的学习，AI 给出三次函数 f（x）=x³-3x ，要求学生通过求导确定单调区间。系统会重点监测学生解不等式 f^′（x）>0 的过程，并在适当时机提出拓展性问题："如果函数中包含参数k，如 f（x）=kx³-3x ，单调区间的判定会有什么变化？"

环节3：AI 变式训练

在巩固提升环节，AI 系统基于实时学情分析，为不同水平的学生推送个性化的变式训练。对于基础薄弱的学生，系统会提供结构化的基础题组，如判断线性函数、简单二次函数的单调性，并辅以分步解题指导。对于掌握较好的学生，则推送含参函数、复合函数等更具挑战性的问题，如"讨论 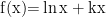在不同 k值下的单调性"。AI 系统会动态调整题目难度，当学生连续答对时自动提升难度，遇到困难时则提供相似但更简单的辅助题目。

环节4：总结与反思

在课堂总结阶段，教师组织学生分组汇报探究成果，AI 系统实时将各组的解题思路和关键步骤整合成可视化的思维导图，清晰展现定义法和导数法的内在联系与应用场景。教师结合 AI 生成的学情分析报告，重点强调易错点，如"使用导数法时容易忽略函数的定义域限制"、"含参函数讨论时分类标准不完整"等共性问题。最后，AI 系统为每位学生生成个性化的学习诊断报告，推荐针对性的课后练习，形成完整的教学闭环。

三、结论

生成式 AI 为问题驱动教学提供了强大支持，尤其在函数单调性等抽象概念的教学中，能有效增强课堂互动性与针对性。未来可探索 AI 与更多数学主题（如三角函数、数列）的结合，推动智能化数学教育的发展。

参考文献

[1]李永莲.走出“模型”定式回归概念本源——以高中数学“函数的单调性”为例[J].数学教学通讯，2025，（03）：38-39+65.

[2]陈李志.基于问题导向的高中数学教学实践与思考——以“函数的单调性”教学为例[J].数学教学通讯，2024，（36）：27-29.

[3]徐海锋.“生成式 AI+数智资源”赋能高中数学课堂教学的探索[J].教育传播与技术，2024，（06）：62-67+73.