摘要：为了使光伏最大功率点算法兼顾稳态精度和跟踪速度，本文在现有变步长电导增量法基础上提出了一种改进型方法，并通过仿真实验验证其可行性。仿真结果表明，改进型变步长电导增量法的动态响应速度更快，显著提升了系统的跟踪精度和动态性能。

关键词：电导增量法；光伏最大功率点；模型

引言

为了最大限度地提高光伏系统的发电效率以及能量利用率，就需要实时调整光伏电池的工作点，让其一直稳定在最大功率点附近运行，此过程称作最大功率点跟踪技术，而电导增量法是借助实时计算并对比光伏阵列的电导与瞬时电导的变化量来判断工作点位置，理论上在达到最大功率点时能达成无静差跟踪，有效克服了扰动观察法存在的固有振荡缺陷，拥有更高的跟踪精度与稳定性。

1 光伏电池的数学模型与最大功率点跟踪

太阳能电池的电能转换效率主要取决于半导体材料的特性，其中光的强度和温度是影响电池性能的关键因素，所以输出电压电流的数字模型为：

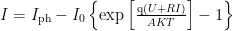
其中，T 是热力学温度，I 是光伏电池输出电流，U 为光伏电池的输出电压，A 为 P-N 结的曲线常数，I0 是二极管反向饱和电流，k 是玻耳兹曼常数，q 为电子电荷。依据上述模型可以发现，温度与亮度在影响太阳能电池输出特性方面并非线性的，其特性如图1 所示。

图1 光伏模块输出电流－电压和输出功率－电压特性图

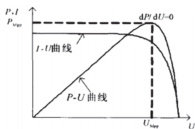
在太阳能电池输出功率达到峰值的情况下，在相应的光强以及温度条件之时，输出电压与电流相乘所得到的数值达到最大，这样一种特定的工作状态被称作最大功率点（MPPT），鉴于光伏组件的输出特性会受到光照强度、温度以及负载变化的作用，其最大功率点会呈现动态变化的情况。为了提升光伏系统的整体效率并且降低能源成本，需借助 MPPT 控制技术对工作电压或者电流进行实时调整，让系统始终处于最优功率点附近开展工作 [1]。

2 MPPT 算法对比研究

2.1 传统的定步长电导增量法

恒定步长电导增量法是一种基于光伏电池输出功率－电压曲线斜率特性的最大功率点跟踪算法，其核心原理是通过实时计算功率对电压的一阶导数来判断系统工作点与最大功率点的相对位置，光伏电池的输出电压功率的一阶导数为：

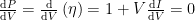
当 dP/dV=0 时，系统处于 MPP；若 dP/dV<0 ，表明 MPP 位于当前工作点右侧，需降低电压追踪；若 dP/dV>0 ，则 MPP 位于左侧，需提升电压。相较于扰动观察法（P&O），INC 法能更精准地锁定 MPP，避免了在MPP 附近的振荡现象，但其跟踪性能受固定步长制约，较大步长虽能加快动态响应速度，但会导致稳态精度下降；较小步长虽提高稳态精度，却会延缓跟踪速度 [2]。

2.2 传统的变布长点导增量法

传统变步长电导增量方法里，光伏电池输出功率 - 电压（P-V 曲线）的斜率特性在最大功率点两侧有明显不同，为优化跟踪性能，常凭借计算斜率绝对值也就是 |dP/dV| 来调整步长，并结合调节系数 M 动态调整电压控制步长，MPP 右侧的曲线斜率绝对值一般大于左侧，系统在 MPP 右侧工作时，较大步长会使工作点快速越过 MPP 直接跳到左侧，甚至出现 dP/dV=0 的误判状况，所以传统变步长 INC 方法仍不能完全消除 MPP 附近的功率波动。

2.3 改进型变步长电导增量算法

改进型变步长电导增量算法借助对步长优化来实现对策略的调整，解决了传统电导增量法在稳态状况下跟踪速度、精度以及功率损耗之间所存在的矛盾，此算法的关键在于对步长进行动态调整，当光伏系统与最大功率点（MPP）距离较远时，运用较大步长来加快跟踪速度，当逐渐靠近MPP 时，步长会逐渐变小以提升稳态精度。

其理论依据是在最大功率点处功率对于电压的导数等于零，并且该值在 MPP 左侧变化较为平缓，而在右侧由于功率曲线较为陡峭会迅速增大，传统固定步长方法在右侧区域容易因为 ΔP/ΔV 出现突变导致振荡或者发散，而改进算法借助引入 ΔP/ΔV 的自适应权重系数，让步长可与系统动态特性相契合，在平坦区域保持较大步长来加快收敛，在陡峭区域自动缩小步长以抑制超调，图2 是 ΔP/ΔV 曲线相互重叠的P-V 曲线。

图 2ΔP/ΔV 曲线重叠的P-V 曲线

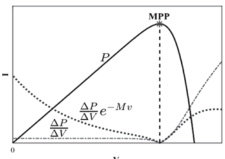
此方法借助实时测量光伏系统的增量电导与负瞬时电导之间的比值关系，对工作电压的追踪方向实施动态调整，一旦检测到 ΔI/ΔV<-I/V ，这意味着工作点处于最大功率点右侧，系统会依据 ΔI/ΔV 的绝对值当作自适应步长来递减电压，相反，当 ΔI/ΔV>-I/V 时，便按照相同规则递增电压。这样的非线性步长设计，能让算法在远离 MPP 时运用较大步长迅速逼近，在接近 MPP 时自动减小步长以抑制振荡，和传统固定步长电导增量法相比较，其步长值与系统当前工作点和 MPP 的偏离程度成比例，保留了电导增量法的跟踪精度，又依靠动态步长机制提升了追踪速度，在光照快速变化的条件下呈现出更优的动态响应特性。

3 仿真实验结果

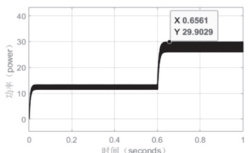
为验证改进型变步长电导增量法的控制成效，本研究依托 Matlab 平台构建了光伏发电系统仿真模型，并就光伏电池的最大功率点跟踪问题展开了详尽的对比仿真分析，实验伊始对传统变步长电导增量法给予测试，在光照强度从 500W/m² 呈阶跃变化至 1000W/m² 且温度恒定为 25°C 的情形下，系统于 0.6 秒后功率输出渐渐趋于稳定。仿真波形显示该方法存有较大的功率振荡现象，并且在动态响应过程中出现较长的调节时间，这意味着传统方法在跟踪速度以及稳态精度方面有优化余地，如图3 所示。

图3 传统变步长增量电导法仿真曲图

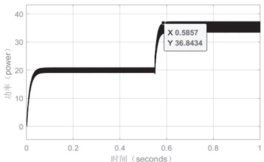
改进方案引入了动态调整系数 M，其预设值是 0.05，在相同环境状况下能把稳定时间缩短到 0.58 秒，最大功率输出从 29.9029W 提升到了36.8434W，进一步分析后发现，改进算法借助自适应调整步长变化率，在光照突变时运用较大步长加速跟踪，临近最大功率点时会自动减小步长来抑制振荡，如 4 图所示。对比实验数据显示，改进后的方法让响应速度提升了 3.3% ，还依靠优化步长调节机制使功率波动幅度降低了约 40% ，证实了其在动态性能以及稳态精度方面有双重优势。

图 4M=0.05 改进型变步长增量电导法仿真图

4 结论

本文在传统电导增量法的基础上进行改进，提出了一种基于指数衰减函数的变步长电导增量 MPPT 控制方法，仿真结果表明，相较于传统方法，改进后的算法在跟踪速度、稳态精度和抗扰动能力方面均有显著提升，有效提高了光伏系统的能量转换效率。

参考文献

[1] 张东宁 . 基于改进电导增量法的光伏最大功率点跟踪策略研究 [J].太阳能学报 ,2022,43(08):82-90.

[2] 邵磊 , 吴金泽 , 孙文涛 , 等 . 基于改进型电导增量法的光伏最大功率点跟踪 [J]. 电子测试 ,2021,(19):71-73+59.