摘要：整式运算作为初中代数的核心内容，是学生后续学习分式、方程、函数等知识的重要基础。本文基于初中学生整式运算的学习现状，通过对作业、测验及课堂反馈中典型错误的收集与分析，梳理出概念混淆、法则误用、运算顺序错乱、符号处理失误等主要错误类型。针对这些问题，结合北师大版初中数学教材的编排特点，提出夯实概念基础、强化算理理解、规范运算流程三大规避策略，并通过具体教学实例说明策略的实践应用，旨在为提升初中整式运算教学质量、促进学生运算能力的稳步发展提供参考。

关键词：初中数学；整式运算；错误类型；规避策略

整式运算贯穿初中数学七年级至八年级的教学过程，其掌握程度直接影响学生数学学习的自信心与后续知识的接受效果。然而，实际教学中发现，学生在整式的加减、乘除、幂的运算等环节频繁出现错误，且错误具有普遍性、重复性等特点，成为制约学生数学成绩提升的突出问题。深入分析错误成因，探寻科学有效的规避策略，是提升整式运算教学效率的关键。本文立足学生学习现状，结合北师大版教材“注重知识生成、强调应用实践”的编写理念，对整式运算错误类型进行系统梳理，重点探究针对性规避策略，为初中数学教师提供教学实践参考。

一、初中整式运算主要错误类型梳理

通过对七年级（上）“整式的加减”、七年级（下）“幂的运算”“整式的乘除”等章节学生作业、单元测验及课堂练习的抽样分析，发现学生的错误主要集中在以下四类：一是概念混淆类，如对单项式系数与次数、同类项定义的理解模糊，导致合并同类项出错；二是法则误用类，如幂的乘方与积的乘方混淆、单项式乘以多项式漏乘项；三是符号处理类，如去括号时忽略符号变化、负数乘方符号判断错误；四是运算顺序类，如在混合运算中先算乘方再算乘除的顺序混乱，或忽略括号的优先性。这些错误既反映了学生对基础知识的掌握不扎实，也暴露了教学中对算理理解和运算规范的引导不足。

二、整式运算错误的规避策略

（一）夯实概念基础，建立清晰知识体系

概念是运算的前提，学生运算错误的根源往往在于对核心概念的理解模糊。因此，教学中应注重概念的形成过程，通过具象化、对比化的教学方式，帮助学生准确把握概念的本质属性，建立清晰的知识关联，从源头规避错误。

例如，在教学北师大版七年级上册“整式的加减”中，夯实概念基础可这样开展：讲解“同类项”核心概念时，摒弃直接给出定义的方式，先呈现“3x²y、5xy²、-2x²y、4xy”等代数式，让学生分组观察字母、字母指数的特征，自主归纳出“所含字母相同，且相同字母的指数也相同”的同类项本质；再通过对比辨析，如标注“3x²y 与 5xy² 因字母指数不同非同类项”，强化概念认知。在合并同类项环节，结合“用小棒拼长方形”的具象化操作，让学生理解“合并同类项本质是合并系数，字母及指数不变”的原理，同时梳理“整式加减 Σ=Σ 去括号 + 合并同类项”的知识脉络，通过概念关联图建立清晰体系，从源头避免因概念混淆导致的运算错误。

（二）强化算理理解，摒弃机械记忆法则

整式运算的法则是基于算理推导得出的，学生若仅机械记忆法则而不理解其本质，极易出现法则混淆、应用失误的问题。教学中应注重引导学生参与法则的推导过程，明确法则的适用条件和逻辑依据，让学生“知其然，更知其所以然”，从根本上提升运算的准确性。

例如，在教学北师大版七年级下册“幂的运算”中，强化算理理解可这样实施：讲解“同底数幂相乘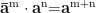（ ）”时，摒弃直接告知法则的方式，先引导学生用乘方的定义拆解算式，如 2³2⁴=(2×2×2)×(2×2×2×2 ），让学生直观看到 3 个 2 与 4 个 2 相乘，本质是 7 个 2 相乘，由此自主推导出指数相加的法则；针对“幂的乘方”与“积的乘方”易混淆的问题，同样通过定义拆解、举例验证的方式，让学生明确前者是“指数相乘”、后者是“各因式分别乘方再相乘”的逻辑依据，而非死记公式。同时结合错题辨析，如对比 a³⋅a² 与 (a³)² 的运算差异，让学生从算理层面解释错误原因，真正摆脱机械记忆，做到灵活应用法则。

（三）规范运算流程，强化细节纠错训练

学生在整式运算中常因步骤不规范、忽略细节（如符号、括号）导致错误，因此，教学中应建立标准化的运算流程，通过“分步训练—细节标注—错题复盘”的方式，培养学生严谨的运算习惯，减少细节失误。

例如，在教学北师大版七年级下册“整式的乘法”时，落实“分步训练—细节标注—错题复盘”流程可这样落地：分步训练时，将“（2x-3） (x+4 ）”这类整式乘法拆解为“单项式乘多项式分步展开 $$ 合并同类项”，要求学生每一步单独书写，不跳步；细节标注环节，让学生用红笔圈出负号、括号等易错点，如在因式分解“- ∂⋅X²+6X-9 ”时，标注“首项负号需先提取”“完全平方公式中首尾项符号一致”；错题复盘则引导学生建立专属错题本，标注错误类型（如符号漏变、括号展开不全），每周复盘同类错题，对比正确步骤与自身错误，通过反复强化细节关注，逐步规范运算行为，降低因步骤疏漏导致的计算错误。

三、结语

整式运算的准确性是初中数学核心素养的重要体现，其教学质量直接关系到学生代数知识体系的构建与后续学习的进阶。本文基于北师大版教材编排逻辑，梳理出概念混淆、法则误用、符号失误、顺序错乱四类典型错误，针对性地提出夯实概念、强化算理、规范流程三大规避策略，并通过具象化教学实例明确了实践路径。教学中，教师需立足学生认知规律，摒弃机械训练，以概念本质理解为根基、以算理逻辑推导为核心、以规范流程养成为保障，帮助学生形成严谨的运算思维。唯有如此，才能从根本上减少整式运算错误，提升学生数学运算能力，为其后续分式、方程、函数等知识的学习筑牢基础，助力学生数学核心素养的全面发展。

参考文献

[1] 杨健伟 . 依托项目式教学提升初中数学教学效果的路径—以“整式的乘除”为例 [J]. 数理化解题研究 ,2025,(29):39-41.

[2] 吴晓莉 . 整体代入法在代数式求值中的高效解题路径——以整式运算为例 [J]. 数理天地 ( 初中版 ),2025,(20):36-37.