打开文本图片集

摘要：本文通过诗句、“龟兔赛跑”寓言故事、刘徽的”割圆术“及《庄子。天下篇》中的”截杖问题”引出极限的概念，让学生在体会数学中的美学和文学的同时，激发学生的民族自豪感和爱国情怀，培养学生努力奋斗的精神；通过数列极限的生活实例，提高学生分析问题、解决问题能力；通过普遍联系的观点，培养学生正确的人生观和价值观。本文融课程思政之“盐”于数列极限之“汤”中，既响应国家号召，又提高了职业院校学生学习数学的积极性。

关键词：课程思政；数列极限教学；实施

一、问题提出

近年来，课程思政与课程教学相融合已上升为国家战略。《高等学校课程思政建设指导纲要》明确了理学类课程思政建设的重点，即要在课程教学中把马克思主义立场观点方法的教育与科学精神的培养结合起来，提高学生正确认识问题、分析问题和解决问题的能力。实现新的课程教学目标，既要发挥教师的指导作用，又要发挥教师在教学过程中促使学生积极主动学习的载体作用。如何在数列极限教学中恰当的融入思政元素，使学生在自然理解掌握所学知识的同时，融思政之“盐”于数列极限之“汤”中，引起学生情感的共鸣，是当前每一位数学任课教师应该考虑的现实问题。

目前，由于职业院校高等数学任课教师课程多，任务重等诸多原因，大部分教师在教学中仍采用传统的教学方式，更倾向于课本知识的单纯传授，学生学习压力大，考试结果不理想，挂科率比较高，不符合教育的本质。课程思政与课程教学相融合，对每位课程教师提出了更高的要求，即让学生在自然轻松的状态下主动掌握所学知，在良好的教学情景中实现思政教育，既提高学生的学习热情，又激发学生的求知欲，同时对学生进行价值引领。

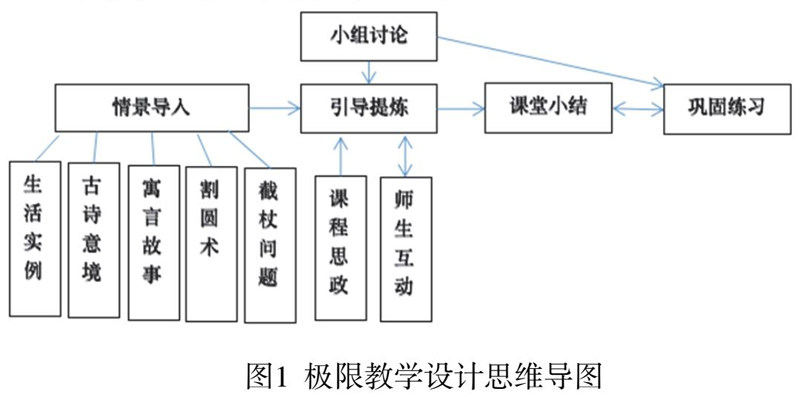
二、教学设计思维导图（如下）

三、教学设计

（一）教学背景

“高等数学”课程是我校的一门公共基础课，总学时120学时，相对于学生基础而言，学习难度偏大，学生整体缺乏学习兴趣，又由于高等数学中的相关概念比较抽象，难于理解，极大挫伤了学生学习的积极性。数列极限概念是高等数学教学中的重要概念，通过案例引导学生理解其通俗化的定义比较简单，理解数列极限的定义并用数列极限的定义来证明极限式，是数列极限教学中的难点。若数列极限教学中恰当地融入课程思政，则能实现在提高学生学习兴趣的同时，让学生更好的理解和掌握所学的知识。

本次课的授课对象为我校本科大一年级现代物流管理专业学生，学生男女比例相当，学生整体性格活波，善于与老师沟通交流，这是开展本次教学的优势；劣势是学生的整体数学基础不扎实，缺乏学好高等数学的信心，对数学纯概念的学习有畏难情绪。

（二）教学目标

知识目标：理解数列、数列极限的概念，掌握数列极限的计算方法。

能力目标：通过极限思想的典型案例，培养学生归纳总结、提炼规律的能力；通过具体的数列极限的计算，培养学生善于观察、分析问题和解决问题的能力；通过任务驱动，培养学生抽象概括及自主学习的能力。

思政目标：引导学生积极勇敢，乐观向上；培养学生的探索、拼搏精神和爱国情怀，鼓励学生树立远大理想并砥砺前行。

（三）教学重点和难点

教学重点：数列极限概念的理解，包括通俗化定义和数列极限的定义；数列极限的计算和用数列极限的定义证明数列极限式。

教学难点：理解数列极限的定义，并能用数列极限的定义证明数列极限式。

（四）教学过程

1.情景导入：创造愉悦的学习环境，提高兴趣

（1）生活实例导入

生活中具有极限思想的案例比较多，例如教室的容量、水杯的容积、气球的充气量等等，教师还可以在教学多媒体课件中插入一些生活实例的图片，让学生自己找出每幅图片中所蕴含的极限思想。

（2）古诗词导入

中国古代诗词文化源远流长，博大精深，以韵律、语感、节奏为主流，营造一种朦胧的意境。古诗词中融入极限思想的诗句比较多，举例如下：“百尺竿头须进步，十方世界是全身”；“大鹏一日乘风起，扶摇直上九万里”；“长风破浪会有时，直挂云帆济沧海”；“路漫漫其修远兮，吾将上下而求索”，“其大无外，其小无内”等等。

（3）经典案例刘徽“割圆术”导入

魏晋时期数学家刘徽首创“割圆术”，为计算圆周率建立了严密的理论和完善的算法。割圆术思想：割之弥细，所失弥少，割之又割，以至不可割，则与圆周合体而无可分矣。教师在黑板上作圆内接正多边形的同时，诵读割圆术思想，并加以解释引导，圆内接正多边形边数趋向于无穷大时，圆内接正多边形面积趋向于圆的面积。枯燥的数学注入文学色彩，必然能激起学生学习的兴趣。

然后，教师还可以给学生布置课堂任务：了解刘徽的个人事迹。通过了解刘徽的成长经历和个人成就，激发学生的民族自豪感和爱国情怀，培养学生努力奋斗的精神。此外，教师还可以分享刘徽割圆术思想的启发：生活中石匠打磨石块，引导学生在日常生活中善于观察，培养学生认真钻研，积极进取。

（4）经典案例“截杖问题”导入

《庄子.天下篇》中的“截杖问题”，也是最经典的极限思想代表。截杖问题思想：一尺之棰，日取其半，万世不竭。一尺长的木棰每天截取原长度的1/2，永远都截不完。截杖问题的实质是一个以1/2为公比的等比数列，如果以天数为自变量，在天数趋向于无穷大的时候，木棰的长度趋向于0.

（5）寓言故事“龟兔赛跑”导入

“龟兔赛跑”是经典的寓言故事，结局是兔子因为各种各样的原因输给了乌龟。当兔子发现乌龟快到终点的时候，兔子追赶乌龟的过程，实质也是极限思想的体现，即随着时间的推移，兔子和乌龟之间的距离无限接近的过程。

通过“割圆术”和“截杖问题”两个经典案例，让学生开展小组讨论，引导学生总结归纳这两个极限思想的共性：自变量趋向于无穷的时候，因变量趋向于一固定的常数。这样，同学们很容易理解总结出极限通俗化的定义：自变量趋向于无穷时，因变量趋向于一固定的常数，这一固定的常数，我们称为自变量趋向无穷时的极限。学生在对极限思想有一个形象化了解的同时，也为后续的教学提供了准备。

2.学生主体，教学互动，让学生在自然轻松的环境下掌握主要知识点

（1）提出问题，学生自学

该环节在建好教学班级群后，每次上课前将问题发到教学班级群，提醒学生自主学习。课堂上安排5分钟通过小组讨论按问题展开学习。数列极限的问题提纲如下：问题1：什么是数列？什么是数列的通项或一般项？问题2：数列极限的定义是什么？怎么证明数列极限式？问题3：数列的极限怎么计算？生活中有哪些数列极限的案例？如何理解？

在该例题的基础上，引出话题：将来如何理财？在学生中展开讨论，激励学生认真学习，积极向上，树立正确的人生价值观。

（3）课堂小结，强调重点，同时布置练习和作业

数列极限教学小结：（1）结合生活实际理解极限的概念，参透数列极限的定义；（2）掌握数列极限的计算方法，在极限计算的过程中，提高分析问题、解决问题的能力，同时通过观察、思考，掌握抽象概括的能力。学习重点是数列极限的证明及数列极限的计算。

四、结语

本文将生活实例、古诗鉴赏、寓言古诗以及经典案例引进课堂，契合所授教学知识点，既提高了学生学习的兴趣，活跃了课堂氛围，又响应了国家的号召。教学过程中充分发挥学生的主体作用，通过案例分析、任务驱动、自主学习及小组讨论等方法，改变了传统的高等数学教学模式，充分发挥教师的引导和载体作用，实现了知识目标、能力目标和思政目标的多目标规划问题。

参考文献：

[1]黄新宇，王修建，岳芹，课程思政元素融入高等数学的教学研究-以数列极限为例[J]，浙江万里学院学报，第33卷第4期间，2020年7月101-104页

[2]李继成 朱晓平，高等数学 （上）[M]， 北京：高等教育出版社，2021：007

[3]李秀林，李淮春，辩证唯物主义和历史唯物主义原理[M]，北京：中国人民大学出版社，1984：218

重庆市职业教育教学改革研究一般项目资助。项目名称：《课程思政背景下智慧课堂融入高等数学模块化教学的探索与实践》；项目编号：Z213009。