
- 收藏
- 加入书签
轮椅竞速运动员临界速度模型的构建与验证:基于六组恒定速度测试的疲劳动力学分析
关键词 临界速度 无氧工作能力 速度—疲劳时间关系 最大速度 轮椅竞速
中图分类号:G804 文献标识:A 文章编号:1009-9328(2024)12-250-03摘 要 轮椅竞速起源于第二次世界大战后伤残士兵的康复运动,是一项对运动员有氧能力要求极高的体育项目。临界功率理论是评估人体有氧能力的经典方法。目前,已有大量研究采用临界功率模型预测不同运动项目(如游泳、自行车、赛艇等)运动员的训练效果、运动表现及运动潜力,并取得了一定的预测效能。同时,利用临界功率理论评估运动员有氧能力的优势在于测试过程简便且易于操作,且不会对受试者造成任何运动损伤。当前的研究尚缺乏通过临界功率理论直接构建轮椅竞速运动员速度—疲劳时间关系模型的针对性研究。本研究旨在探究:(1)采用六组不同恒定速度(力竭速度测试中力竭速度的 80% 、 85% 、 90% 、 95% 、 100% 、 105% )下的全力运动测试建立临界速度模型的有效性;(2)评估上述不同临界速度模型在轮椅竞速中的应用价值;(3)观测六组运动测试所得参数对受试者5000 米实际运动表现的预测效能,以及其对5000 米竞赛策略制定与训练方案设计的指导意义。
轮椅竞速起源于二战伤残军人的康复运动,1964年成为残奥会项目。作为上肢主导的周期性项目,其对运动员有氧能力要求极高 [1-4]。临界功率理论是评估有氧能力的经典方法,已在游泳、自行车等项目中得到验证 [5-7]。当前缺乏针对轮椅竞速的临界速度模型研究。本研究旨在:(1)验证六组恒定速度测试构建模型的可行性;(2)评估模型应用价值;(3)预测 5000米运动表现。
一、研究对象与方法
(一)研究对象
选取 10 名 T54 级男子轮椅竞速运动员(含 1 名残奥选手),年龄 25.30±4.10 岁,体重 60.8±5.34kg ,签署知情同意书。
(二)研究方法
1. 计时测试。在标准田径场进行 1500 米(提供初始速度)和 5000 米(实际表现对照)测试,使用秒表记录成绩。
2.力竭速度测试。以1500米速度的 85% 为初始速度,每2 分钟递增1km/h 至力竭,记录最终速度(EV)。
3. 恒定速度测试。进行 EV 的 80% 、 85% 、 90% 、95% 、 100% 、 105% 六组全力运动,记录运动成绩、心率和血乳酸。
4. 最大速度测试(Vmax)。通过100 米行进间测试获取 Vmax。
(三)统计学方法
采用SPSS 22 分析数据,显著性水平 P<0.05 ,使用 Bonferroni 校正。通过公式 1-5 计算 CV 与 AWC,线性回归比较预测值与实际值。
二、研究结果
(一)计时测试、力竭速度测试与最大速度测试结果
力竭速度(EV)为 9.72±0.31m/s ,最大速度(Vmax)为 10.13±0.53m/s 。长距离项目中,1500 米平均速度
6.90±0.49m/s ,5000 米平均速度 8.66±0.26m/s. 。
(二)六组恒定速度运动测试指标变化
当运动强度从 80%EV 提升至 105%EV 时:运动时间从 224.32±120.41 秒降至 48.87±18.56 秒 (P<0.001); 运动距离从 1838.19±986.73 米缩减至 434.36±164.97 米( :P<0.001: );运动后心率由 193.70±12.70 bpm逐 步 下 降 至 167.90±10.15 bpm( (P<0.001⋅) ); 血乳酸浓度维持在 10.33~11.64mmol/L 范围,各组间无统计学差异( ΔP>0.05 ),但均显著高于静息值2.33±1.360001/L ( Φ⋅P<Φ0.001 )。
(三)双参数模型分析
三种速度—疲劳时间关系模型均显示良好拟合:D-T模型 R2=0.99 (最优);V-T 模型 R2=0.97 ; V-1/T 模型R2=0.94 ;临界速度(CV)与无氧运动能力(AWC)在各模型间无显著差异( .P>0.05 )。
(四)模型参数比较
双参数模型中:线性D-T 模型: CV=8.29±3.06m/s ,AWC=373.12±175.40m ; V-1/T 模 型: CV=8.34±3.02m/ s, AWC=359.71±181.70m ; 非 线 性 V-T 模 型:CV=8.26±3.03m/s , AWC=390.42±170.23m ;三参数模型 CV( 7.59m/s )显著低于双参数模型( P<0.05 ),其 AWC(762.10m)为双参数模型的 2~3 倍( (P=0,003 )。
(五)模型间差异分析
三种主要模型参数对比:CV 值:双参数非线性模型8.26a vs 三参数模型 7.03b vs 指数模型 8.92c(a,b,c间 P<0.05 );Vmax:三参数模型 9.63±0.42m/s 显著高于指数模型 9.02±0.31m/s ( P=0.027 );拟合优度:三参数模型 R2=0.998 最优,指数模型 R2=0.986 次之。
(六)5000 米速度预测效能
模型预测与实际值( 8.66±0.26m/s )相关性:双参数模型组相关系数 0.94-0.96( 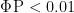 );三参数模型相关系数 0.78-0.88( ⋅P<0.05 );CV 与实际 5000米速度相关性:双参数模型 0.94-0.97 vs 三参数模型0.32-0.47。
);三参数模型相关系数 0.78-0.88( ⋅P<0.05 );CV 与实际 5000米速度相关性:双参数模型 0.94-0.97 vs 三参数模型0.32-0.47。
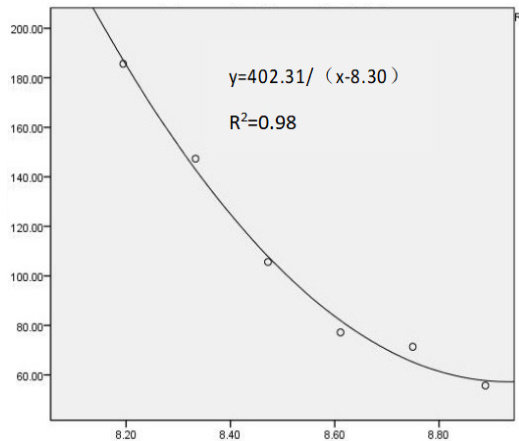
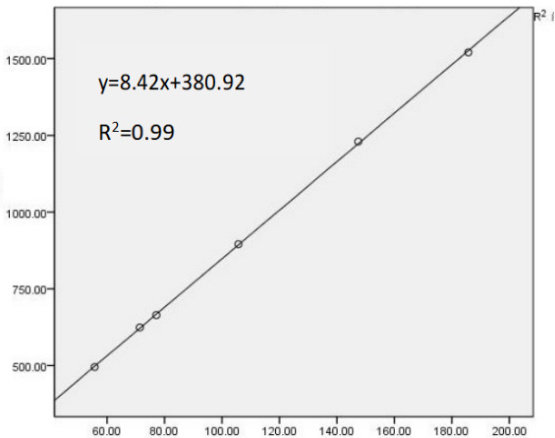
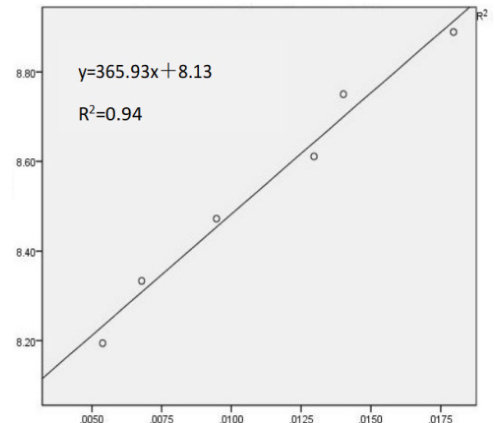
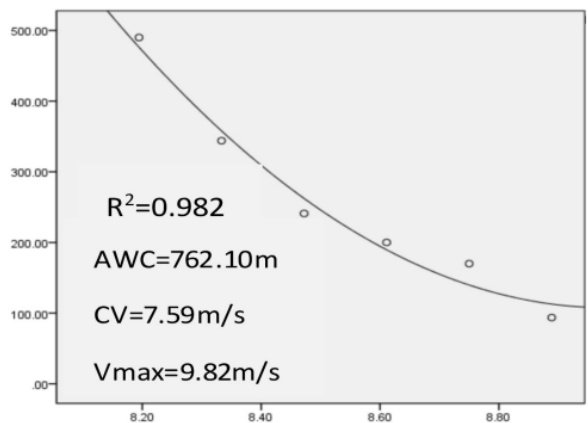
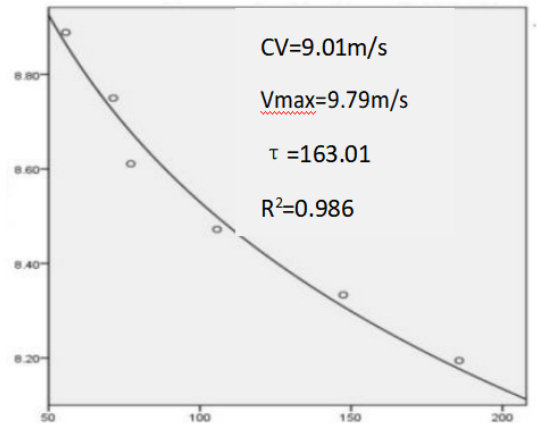
图5 三参数距离—疲劳时间指数关系模型图
研究结果与 Laurent Bosquet 和 Hill 等人的发现具有一致性,证实双参数模型在耐力运动表现预测中的优势,而三参数模型在无氧能力评估方面显示出更高的灵敏度。
三、讨论
通过三种双参数数学模型的对比,本研究对T54 级轮椅竞速运动员在场地运动中的速度—时间关系模型进行研究。由于T54 级运动员神经生理系统的损伤会影响运动员的运动耐受性,故需考虑速度—时间关系模型的可行性及对健康的负面影响。因此,本研究为此类人群速度—时间关系的适用性提供依据。基于不同数学模型,我们发现在对比三种模型时存在准确性差异,如双参数距离—疲劳时间线性模型( ⋅R2=0.99 )、双参数速度 -1/ 疲劳时间线性模型( 1R2=0.94⋅ )及双参数速度—疲劳时间非线性模型( ⋅R2=0.97 )。总体而言,所建立模型的拟合优度均较高,但当对各模型单独分析时,双参数距离—疲劳时间线性模型在所有受试者中的拟合优度最高( ⋅R2=0.99 )。
在既往研究中,存在较多关于双参数距离—疲劳时间模型对轮椅运动员不同项目运动准确性研究。例如,在轮椅运动员跑步机运动研究中,距离—疲劳时间模型的模型拟合优度为 R2=0.99 ,在户外场地研究中( ⋅R2=0.99 )。此结果与双参数距离—疲劳时间模型的研究结果一致。
此外,三种数学模型导出的CV 无显著性差异。尽管本研究所选的三种模型在数学函数公式上等价。但根据Bergstrom、Nimmerichter 及 Bull 的研究发现,部分腿部参与的运动模型(如自行车、跑步、足球等运动)中CV 的估算存在差异。利用双参数模型,我们可通过场地测试结合简单的Excel 办公软件计算出临界速度与无氧运动能力。值得注意的是,在Karsten 等人2014 年发表的关于自行车运动员实验室与场地临界速度差异的文章中,结果显示实验室估算的CV 值与场地估算值高度一致。本研究支持本文中将实验测试置于场地的可行性。此外,根据Muniz Pumares 等人的研究,可通过临界速度与无氧运动能力的低标准误证明双参数模型的拟合优度。根据 Hill、Stevens 及 Morgan 等人分别于 2005 年及 2019年的研究,可通过超高强度运动(运动持续时间为 2~15 分钟)建立双参数速度—疲劳时间模型。
本研究结果如下:6 组运动测试的设置符合人体能量代谢规律;不同模型所得参数(临界速度、无氧工作能力、最大速度等)存在一定差异;发现三参数非线性模型的最大速度(Vmax)计算值显著高于指数模型( (P<0.001⋅ ),且两模型的最大速度(Vmax)计算值均显著低于实际最大速度;双参数模型、三参数模型及指数模型计算的5000米速度与实际5000 米速度均存在较高相关性(双参数模型 P=0.94 、0.95、0.96;三参数模型 P=0.88 ;指数模型P=0.78 )。但相比之下,双参数模型对5000 米运动表现的预测效果优于三参数模型及指数模型。
四、结论与建议
本研究通过不同恒定速度下的六组全力运动测试,可建立T54级男子轮椅竞速运动员速度—疲劳时间(V-T)模型;利用临界速度测试模型可对 T54 级男子轮椅竞速运动员的 5000 米成绩进行预测;通过不同数学公式,本文得出三类速度—疲劳时间关系模型(双参数速度—疲劳时间非线性模型、三参数速度—疲劳时间非线性模型及三参数速度—疲劳时间指数模型),发现双参数速度—疲劳时间关系数模型在预测 T54 级男子轮椅竞速运动员运动表现方面优于三参数模型;通过双参数速度—疲劳时间关系模型可为轮椅竞速教练员制定 5000 米竞赛策略及长距离运动员训练计划提供新手段。
参考文献:
[1]KennedymDJ, Bell GJ. A comparison of critical velocity estimates to actual velocities in predicting simulated rowing performance. Can J Appl Physiol. 2000;25:223-235.
[2]Scruton J : Sir Ludwig Guttman ∵ Creator of a world sportsmovement for the paralyzed and other disabled . Paraplegia 54(3) :229-233, 1983 . 17(01) :52-55, 1979.
[3]JoynermJ, Ruiz JR, Lucia A. The Two-Hourmarathon: Who and When? J Appl Physiol. 2010 Aug 5.
[4]Coutts KD, Schutz RW: Analysis of wheelchair track performances.med Sci Sports Exerc20(02) :188-194, 1988.
[5]Jones AM, Poole DC. Introduction to oxygen uptake kinetics and historical development of the discipline. In: Jones AM, Poole DC, eds. Oxygen uptake Kinetics in Sport, Exercise andmedicine. London, New York: Routledge; 2005.
[6]Burnleym, Doust JH, Vanhatalo A. A 3-min all-out test to determine peak oxygen uptake and themaximal steady state.med Sci Sports Exerc. 2006;38:1995-2003.
[7]Poole DC, Ward SA, Gardner GW, Whipp BJ.metabolic and respiratory profile of the upper limit for prolonged exercise inman. Ergonomics. 1988;31:1265-1279.






 京公网安备 11011302003690号
京公网安备 11011302003690号


