打开文本图片集

摘要：目前，我国全面提倡实施素质教育，同时，提倡减轻学生的学业负担。“变题”的方法和技术成为教学中常用的教学方法。在初中数学中，数学知识较多，要着重培养学生的思维和解题能力，传统教学多使用题海战术展开教学，学生大量做题，自己摸索解题方法，学习效率较低，让学生花费大量时间在数学学科上，学习成绩难以提高。为有效提高学生解题能力，采用“变题”方法展开教学，通过分析“变题”技巧，让学生能够掌握题目变化以及解题思维，进而提升解题能力。

关键词：初中数学;“变题”;解题技巧

初中数学教学重点在于培养学生解题能力，由于学生解题能力较为薄弱，很难灵活应对复杂的题目。基于此，本文先对“变题”的优势进行分析，然后阐述了“变题”方法和技巧。通过讲解“变题”技巧，让学生能够掌握解题思维的变化，有效提高学生举一反三的能力。

一、 “变题”的优势

在初中数学中，“变题”练习具有诸多优势。首先，“变题”是根据学生学习需要进行变化，能够让学生在学习过程中得到针对性训练，能够帮助学生熟练掌握数学知识，在合适的练习时机得到训练，提高练习的效率，让学生能够灵活掌握知识点，形成知识体系。其次，“变题”后，题目之间存在明确的联系点，让学生了解联系点，能够让学生建立题目库，在下次遇到这类题目时能够灵活应对题目。最后，学生直接参与“变题”过程，这对于学生的成长十分关键。教学改革实施后，学生在课堂上占据主体地位，学生的主动参与能够有效激活学生的学习积极性。同时通过引导学生分析题目的变化，让学生可以站在出题人角度上进行考量，有助于让学生了解题目考查的知识点，面对其他题目时能够快速找出合适的解题方法，提高解题速度。变题过程中，教师需要积极关注学生的课堂表现，根据学生的课堂表现了解学生的水平，进而调整“变题”研究的节奏和速度，保证全班学生都能得到解题能力的培养。

二、初中数学教学中“变题”方法与技巧

初中阶段的数学题目虽然相对简单，但是初中数学所涵盖的内容非常丰富，包含很多的概念、公式，定理等内容，如何应用它们去解决问题，以不变应万变，需要我们应用正确的解题方法。比较常用的“变题”方法有数学形式变题、数学内容变题和数学方法变题，针对不同的数学题目应用相应的方法。

（一）数学形式“变题”

数学形式变题主要指数学语言变题和数学图形变题

（1）数学语言“变题”。主要是对初中数学教材中的一些概念、公式、定理等进行符号语言、文字语言的互相转换。例如：同一个一次函数用四种方法表示为：

①语言表示：一次函数

②解析式表示：y=kx+b（k≠0，k，b是常数）

③列表法表示：列x的值对应的函数值y列成一个表来表示的函数关系的方法叫做列表法。

④图像法表示：函数关系的方法叫做图像法。

（二）数学内容“变题”

（2）变条件不变结论的“变题”。主要是指在以一题为基准，对此题的条件进行变换，而所求的结论不变。通过这一系列的题目的练习，使学生形成完整的与这道题所涉及到的相关知识结构。

例如：已知等腰三角形，一腰长为6cm，底边长为9cm，求此三角形的周长。

教师将题目中的条件进行变化，继续启发学生思考如下题目：

1.若等腰三角形的一边长为6cm，另一边长为9cm，求此等腰三角形的周长。（6cm是腰长还是底边长？）

2.若等腰三角形的一边长为6cm，另一边长为12cm，求此等腰三角形的周长。（发现条件有何改变？）

教师引导学生发现：在求解等腰三角形的有关题目时，要考虑等腰三角形的三边是两腰和一底边，同时要考虑满足三角形的三边关系。

（3）既变条件又变结论的“变题”。主要是指在以一题为基准，对此题的条件进行变换同时，而所求的结论也变。通过这一系列的题目的练习，使学生形成完整的与这道题所涉及到的相关知识结构。

以上面的例题为例：已知等腰三角形，一腰长为6cm，底边长为9cm，求此等腰三角形的周长。教师将题目中的条件和结论进行变化，继续启发学生思考如下题目。

1.若等腰三角形的一边长为6cm，周长为18cm，求底边长。

2.若等腰三角形的腰长xcm，底边长为ycm，周长为18cm，你能写出x和y的函数关系式吗？（把问题与一次函数内容进行综合）

通过上面一系列的变题，既有利于学生形成知识体系结构，又有利于提高学生的思维能力和解题能力。

（三）数学方法“变题”

数学方法变题主要指对于同一数学问题从不同的角度寻找不同的方法解决，常见的有图形方法变题和代数方法变题。

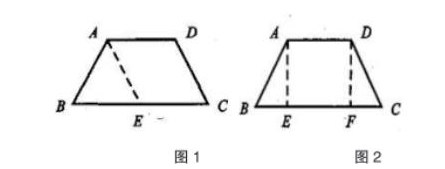
（1）图形方法“变题”。主要针对同一个问题运用不同的图形方法进行解决。例如：证明等腰梯形判定定理“在同一底上的两个角相等的梯形是等腰梯形”。引导学生用多种图形方法进行证明。

证法一：图1，过点A作AE∥DC交BC于点E，利用平行四边形的判定及性质得到AE=DC，利用平行线的性质得到∠AEB=∠C，再利用等角对等边的性质定理得到AE=AB，最后利用等式的性质得到AB=CD。

证法二：图2，作AE⊥BC于E，DF⊥BC于F，利用平行四边形的判定及性质得到AE=DF，再利用全等三角形的判定“AAS”得到△AEB≌△DFC，从而得到AB=CD。

（2）代数方法变题。主要针对同一个问题运用不同的代数方法进行解决。

例如：在分解二次三项式x2+px+q时，可以运用十字相乘法、双十字相乘法、添项、拆项法，换元法等来解决。通过以上的这种变式，达到“万变不离其宗”的目的，有利于培养学生的迁移能力，有利学生对知识结构的梳理。

三、结语

综上所述，初中数学学科作为初中最重要的学科之一，学生学习难度较高，教师需要从方法和技巧上进行教学，提高学生的能力，培养学生的思维，才能让学生得到成长，能够自如应对多变的数学题目，提高学生的数学成绩。因此教师要积极利用“变题”教学，利用变题技巧提高学生解题能力。

参考文献：

[1]周剑云.“生本教育”理念下的初中数学课堂教学策略的实践与探究[D].杭州师范大学，2020.

[2]邱明朗.刍议初中数学解题教学“变”的魅力[J].数学教学通讯，2019（27）：32-33.