打开文本图片集

平面图形的面积教学是小学阶段图形与几何领域的重要内容。这部分内容的研究多是从概念教学、度量、转化的思想方法进行研究。那么，在面积的学习中，学生的思维起点是什么？通过学习应该达到什么思维水平？学习过程中思维发展有那些困难？教师又应该设计怎样的活动帮助学生达成这样的思维水平？基于上述思考，我们借助范希尔理论对小学教材中面积教学内容进行分析，调研学生面积思维发展水平，以此促进我们更好的进行面积内容教学，帮助学生提升几何思维水平。

一、基于范希尔理论的小学“图形面积”内容思维水平的划分和描述

范希尔理论将学生的几何思维水平划分为五层，分别是视觉（visuality）、分析（analysis）、非形式化的演绎（informal deducation）、形式的演绎（formal deducation）、严密性（rigor）。这五个思维水平既可以用于诊断学生的几何思维水平，也可用于教学活动设计。也是基于这样的认识，范希尔夫妇将几何教学划分为五阶段：学前咨询、引导定向、阐明、自由定位、整合。范希尔理论为设计层级递进的教学和评估阶段教学效果提供了分析框架。

在小学几何内容的学习中主要涉及范希尔几何思维水平的前三个水平。考虑到小初之间的衔接，方便老师们了解学生在后继学习中思维水平的发展方向，我们在研究中加入了第四个水平。依据范希尔几何思维水平划分，我们将小学生“图形面积”的思维水平进行划分，具体如下：

水平0：前认知水平

（1）不能准确的说出比较的是哪儿的大小，有时会将面与长度混淆。

（2）能辨别一些图形面的大小。

水平1：视觉（通过视觉整体感知图形的面积）

（1）能指出或画出图形的面积指的是哪部分的大小；

（2）能观察比较面积大小明显不同的图形面积，但不能以要素来分析图形面积大小；

水平2：分析（能描述出图形面积的相关要素及面积与要素之间的关系）

（1）理解面积单位的含义，能通过直接测量找到图形的面积；

（2）能说出面积组成要素的名称，可以用合适的语言来描述图形面积与要素之间的联系。

水平3：非形式化的演绎（能推导出图形面积的公式并灵活应用）

（1）能通过切割、拼摆等方式进行图形的操作，发现图形面积的计算方法。

（2）理解图形面积的计算方法，能应用面积公式灵活解决问题。

水平4：形式的演绎（能通过严谨的推理或解释说明证实猜想）

（1）学生理解并能解释图形面积计算方法，理解解决图形面积问题必须具备的充分或者必要条件。

（2）能猜测并尝试运用演绎方式证实其猜测。

二、小学数学教材中“面积”教学内容分析

（一）“图形面积”教学内容的思维水平分析

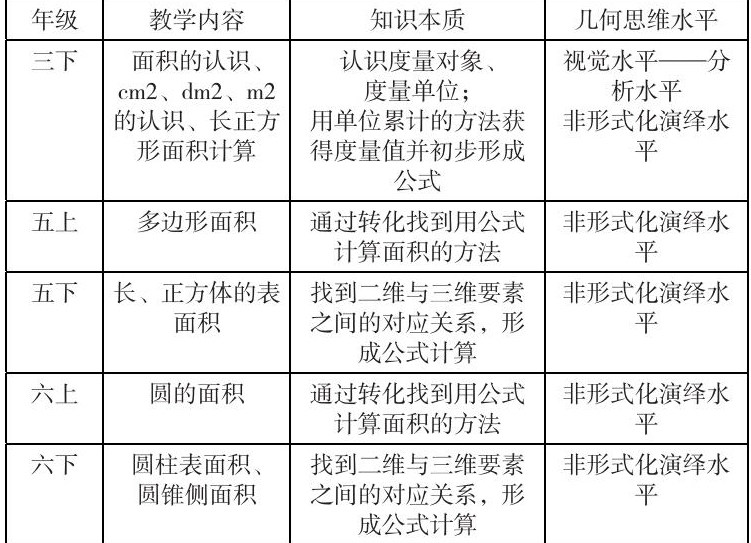
结合前面对小学生“图形面积”的思维水平的划分及教学内容、度量本质的分析，学生在各年级应达到的思维水平分析如下：观察上表不难发现：在第一学段的学习中，学生的思维重点是从视觉水平向分析水平的发展；第二学段是以视觉水平为基础，经历分析水平，并最终达到非形式化演绎水平。学生的整体思维水平的发展符合范希尔的几何思维水平发展理论。

在每个阶段的学习、甚至每课的学习中都遵循着这样的思维水平发展。比如：长方形面积的学习中，先明确研究对象，再探究分析找到每行个数、行数与长和宽之间对应关系，最后形成公式，也是沿着视觉水平——分析水平——非形式化演绎水平发展的。

对比学生对度量本质的理解和思维水平的发展过程，我们发现它们是一致的。从明确度量对象——确定度量单位——获得度量值的学习过程来看，学生的思维也正是沿着视觉水平、分析水平、非形式化演绎水平这样发展的。

（二）“图形面积”教学中促进学生思维发展的关键课时分析

1.“面积的认识”一课是学生在视觉水平发展的关键

学生对面积概念的理解贯穿整个单元的学习。“面积的认识”作为第一课时，是学生从学习长度到学习面积，从一维空间向二维空间转化的开始，是空间形式上“由线到面”的一次飞跃。通过这课时的学习，学生不仅能够通过视觉整体感知图形的面积，还能通过摸一摸、涂一涂准确地指出面积指的是哪部分的大小；能通过观察比较出面积大小明显不同的图形面积；能区分周长和面积。因此，这是学生在视觉水平上发展的关键。

2.“长方形面积”一课是学生在分析水平发展的关键

“长方形的面积”一课是学生探究的第一个平面图形的面积。虽然学生通过探究最终形成面积计算公式，但从学习过程看，公式的形成依赖于用面积单位度量的过程，重点突出的是度量，让学生体会度量的本质。从思维发展来看，这是学生第一次分析长方形面积与相关要素（长、宽）之间的对应关系，这种分析经验是后继探究平行四边形、三角形、梯形等图形面积的基础。因此，这是学生在分析水平上发展的关键。

3．“平行四边形面积”一课是学生在分析水平上突破、最终达到非形式化演绎水平的关键

“平行四边形面积”一课中是以度量为基础，借助几何直观通过转化和推理求出面积计算公式。这一课中转化的思想方法也是后继三角形、梯形、圆形面积探究的关键。对比分析转化前后图形要素之间的对应关系是学生形成公式的关键。因此，这一课是学生在分析水平上突破、最终达到非形式化演绎水平的关键。

4.“圆的面积”是学生第一次完整经历从定性到定量刻画图形的面积

学生在圆的面积研究中很容易发现圆的面积大小和半径有关，也能定性描述出它们之间有何关系。然后是对圆面积的定量刻画，圆面积与对应的半径之间究竟存在什么关系，再通过转化探究出圆的面积公式。前期图形面积的研究帮助学生积累了一定的图形面积与要素之间存在关系的思考经验。学生在圆面积的探究中，才能结合这个图形的特征完整地经历从定性分析到定量刻画的过程，最终形成研究图形面积的方法：明确研究对象（面积指的是哪儿）——分析面积的相关要素（面积的大小和谁有关）——用要素之间的关系表示图形面积（有什么关系）。

三、学生“图形面积”思维水平的整体发展状况

通过对三、五、六年级学生图形面积思维水平的调研，我们发现：

学生在各个思维水平上的发展是相互促进、螺旋上升的

学生在各个思维水平上的发展整体遵循视觉水平、分析水平、非形式化演绎水平的发展顺序，但它们不是截然分开的，而且会相互促进，螺旋上升。

学生在视觉水平上的发展和生活经验密不可分

在正式学习图形面积之前，大部分学生已经达到水平1，能直观感受图形的面及面的大小。在生活中学生有很多平面图形比大小的经验，对“表面”、“面”这些概念是有感受，只不过大部分学生没有接触过“面积”这个词。而且与周长概念的辨别有助于学生进一步面积的概念，建立准确的整体感知。

学生在分析水平、非形式化演绎水平的发展是重点亦是难点

通过调研发现，有些学生学完后对图形面积的分析或计算能存在较大问题，这和学生思维特点、空间观念、逻辑分析能力等都有一定关系。因此，教学中教师需要设计一些有效的活动或手段来帮助学生突破并达到这样的思维水平。

四、促进学生思维水平发展的教学策略

怎样设计有效的教学活动促进学生思维水平的发展呢？通过教学实践，我们试图提炼出一些对提升学生思维水平有效的教学策略，希望对大家的教学有所帮助。

（一）借助学情调研找准学生的最近发展区

通过前测、后测我们分别调研出了学生的思维起点及可能达到的思维水平。但学生思维的发展不是一簇而就的，关于图形面积的思维水平划分及调研情况，能够帮助我们逐层确定好学生的最近发展区。

以《平行四边形面积》一课为例，学生的思维最终要发展到水平3，即推导出平行四边形面积计算公式并能应用其解决问题。依据调研情况，我们将学生的最近发展区逐层设置为：学生做法展示（平行四边形的面积到底和谁有关，底和高还是底和邻边）——指一指哪儿是平行四边形的面积——讨论怎样研究平行四边形面积——数方格、割补活动验证（确认平行四边形面积和它的底和高有关系）——猜想怎样计算平行四边形面积——推导验证猜想——获得平行四边形面积计算公式——应用公式解决问题。这一过程基于学生的思维路径，符合学生的最近发展区，也体现了学生在三个思维水平上的发展。

（二）注重学生参与结论生成过程

从两节课中可以看出，学生要达到水平3，必须经历和达到水平2。为了帮助学生达到并突破这一水平，在《三角形面积》一课中，我们由原来设计的简单的提问“图形的面积和谁有关”调整为让学生经历想转化、动手操作实现转化、对比观察分析联系一系列活动，当学生有体验感受之后再来分析得出面积的相关要素。学生有了行为和思维上的参与，才能对面积的相关要素有所理解和建构，最终提升思维水平。在学生参与的过程中，尤其是讨论的过程中，教师要勇敢的退出来，多让学生说说你是怎么想的？你是怎么想到的？让学生的思维通过语言外化，以说促进学生思维的发展。通过生生交流、师生交流活动，使思维不断碰撞，促进学生思维的积极参与和思维能力的提高。

（三）注重学生推理能力的发展

在这两节课中，学生思维发展最终指向是水平3。因此，推导公式这一教学环节中，学生推理能力的发展是学生思维发展的关键。在这两节课中，让学生借助学案纸画一画、写一写、结合图说一说，在尝试推理的过程中给学生搭建脚手架，使不同层次的学生都能在推导的过程中都能有抓手，进而促进其推理能力的发展。

当然，“转化”在两节课中都是非常重要的数学思想方法。经历转化的过程，感受转化的思想和方法，是学生思维水平发展的助推器。在两节课中，我们将其细化为转化的需求、转化的方法、转化前后的联系，通过活动层层推进，帮助学生积累转化的活动经验。

参考文献：

[1]鲍建生，周超.《数学学习的心理基础与过程》[M].上海：上海教育出版社，2009：4-21

[2]金纯.小学数学教科书“图形与几何”领域比较硏究——基于范希尔理论的视角[D].南京师范大学硕士论文，2015.

[3]郭欣. 小学生对图形与变换内容理解水平的调查研究[D].东北师范大学硕士论文，2015.