打开文本图片集

一、教学内容

人教版小学数学三年级上册第七单元《长方形和正方形的周长》。

二、教学说明

（一）课标要求

《义务教育数学课程标准（2022年版）》明确提出：数学教师应注重对学生几何直观能力的培养与提高。由此可见，如何提升学生的几何直观能力在教学中占有越来越重要的位置。本课将折纸融入教学活动里，以直观的方法运用于课堂教学中，结合“融·乐”课堂教学理念，将学科内部知识融会贯通，使学生在折纸过程中感受几何图形的细微变化，从而促进跨学科的全面学习。同时，注意数形结合，这样可以提高学生直观的几何能力；注重动手操作和练习过程，考查学生的几何直观能力。

（二）学情

长方形、正方形的周长是小学数学三年级上册图形与几何中的教学内容之一。在此之前，学生对长方形和正方形的认识已经有所了解，并且掌握了长方形和正方形的特征；经过独立探究——小组讨论——归纳总结等教学环节，知道了长方形和正方形的周长计算方法，所以将长方形和正方形的周长算出来并不是什么难事。本节课在上一节课的基础下，结合折纸活动，让学生在“玩”的氛围中巩固知识，加深印象。学生学好这一内容，可以为接下来学习长方形和正方形的面积、其它平面图形的周长和面积等几何图形的学习作准备，也可以让学生感受到数学的学习来自生活。

由于小学三年级的学生在学习的过程中自控力不强，并且综合运用知识解决问题的能力有待提高，传统的课堂教学难以激发学生对数学学习的乐趣。因此，在本节课课堂教学中，教师可通过折纸这一直观的操作活动，调动学生学习的积极性，提高学生解决问题的能力。

三、设计理念

折纸活动能把数学学习生活化、趣味化。即折纸活动把数学教学活动与生活中的数学问题联系起来，与几何图形联系起来，唤起学生对数学学习的好奇心，从而为学生提供后续学习的动力。学生在折纸活动中加深对图形、几何的理解，同时，根据课标要求，动手操作，亲身体验知识的形成，以数学思维解题。

四、教学目标

1.结合折纸活动的具体情境，对长方形、正方形的周长进行理解和计算。

2.经过展开折叠、寻找规律等活动过程，培养学生动手操作、独立观察、合作交流、分析推理的能力。

3.教师在引导学生进行折纸活动的过程中，提高学生学习数学的乐趣。

五、教学重难点

在折纸活动中，能运用长方形和正方形的周长公式较好地解决实际问题，计算长方形和正方形的周长。

六、教学准备

教具准备：多媒体课件、折纸若干张。

学具准备：折纸若干。

七、教学过程

（一）游戏引入

1.脑筋急转弯：小新想要将一张细长的纸折成两半，谁知道两次都没折准。第一次有一半比另一半多出一厘米；第二次正好相反，这一半又少了一厘米。请问，两道折痕之间有多宽？

2.教师：大家爱不爱折纸呢？这节课老师要和大家一起来折纸，看看一张小小的折纸里能包含了哪些数学的知识？

设计意图：课堂开始，教师用一个脑筋急转弯引入情景，把抽象的数学课堂变得生动有趣。大部分学生对脑筋急转弯都是比较感兴趣的，会在脑海里想像这一个折纸的情景，从而引发思考“两道折痕之间有多宽？”进而揭示本节课课题“折一折，算一算”。

（二）活动探究

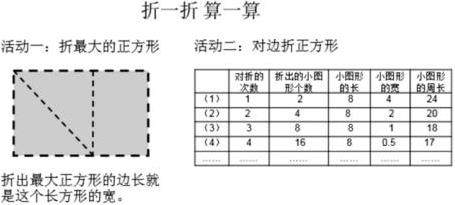
1.活动一：拿出长方形纸，请用这张长方纸折出一个最大的正方形。

（1）折一折，画一画（折完后在纸上用虚线把折出的这个最大正方形画出来）。

（2）思考如何叠成的？如何保证这正方形四角均为直角、四边均相等？

学生在全班面前展示自己的折法。

教师小结：因为正方形对边相等、4个角都是直角。因此，用对角对折的方法能保证折出来的正方形是最大的。

设计意图：在教材几何图形这一单元里，经常会出现在一个长方形里剪下一个最大的正方形这一个情景。这种比较抽象的题目对于小学三年级学生来说是比较难以理解的，而折纸活动在小学数学图形与几何中的应用正好能够让学生直观地接触正方形、长方形等图形。教师将折纸活动与教学内容融为一体，让学生通过折一折、画一画的方式，进一步感知长方形与正方形之间的联系，能使数学基础知识更加丰富。

（3）如果这个长方形的长度为 8cm，宽度为 6cm，请做活动一的练习。（同桌做完再进行沟通）

①折出的正方形边长是（   ），这个正方形的周长是（    ）。

②剩下的图形是一个长方形，这个长方形的长是（  ），宽是（  ），周长是（  ）。

设计意图：这是在第2小题的基础上安排的。学生完成折纸活动后，马上让他们运用长方形、正方形边长的特征解决问题，强化对图形特征的掌握，有利于学生联系数学知识，让学生能在活动中学习，提升学生在数学学习中的参与度和趣味性。

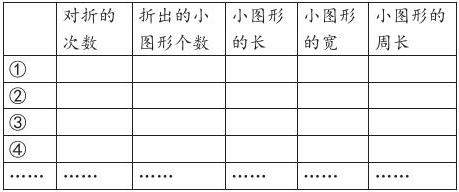
2.活动二：拿出一张正方形纸，按步骤折出一个正方形，并完成表格。已知这张正方形纸边长是8cm。

（1）将这张正方形纸对边折，填在表格对应空白处。

（2）在步骤（1）的基础下，再将纸对边折，并完成表格对应空白部分。

（3）在步骤（2）的基础下，再将纸对边折，并完成表格对应空白部分。

（4）按照规律，如果将纸折4次，这时候会折出几个小图形呢？完成表格。

（5）如果换成超大的纸片，是不是可以无限地折下去？

设计意图：活动二通过同桌合作的方式，鼓励学生互相交流沟通，进行灵感的碰撞。学生通过同桌间分组折纸实践的学习，能够提高独立思考能力和动手实践能力，增加对图形几何学习的印象，从而全面发展。活动二最后提出一个问题引发学生思考，激发学生对折纸活动的好奇心，开拓学生的大脑思维，提升其观察力和思考能力。

3.知识面扩展：如果一张纸足够大，那么它可以一直无限对折吗？

（1）不管拿出来的是哪种纸、多大的纸，对折的次数不会超过9次。

（2）阅读科普小资料：在2011年，美国一所中学的教师和学生将一张接近4000米的纸对折了13次。为了完成实验，他们集体折叠了4 个多小时，在 200 多米长的走廊里放置了纸。13次对折后，纸张达到8192层，刷新了吉尼斯世界纪录。

（3）观看科普小视频：一张纸最多可以对折多少次？

设计意图：数学离不开生活。小学三年级的学生性格活泼，对生活中的许多事物都有很大的好奇心。教师在数学课堂的教学中融入一些生活小知识和科普性小视频，不仅可以提高学生上课的专注力，而且可以让他们对数学这门课程的兴趣更加浓厚，同时可以营造轻松愉快的学习氛围。

（三）巩固练习

1.一块长方形布料长5米，宽4米。

（1）阿姨要在这块布中裁出一个最大的正方形，这个正方形的边长是（    ）米。

（2）剩下的图形是一个（   ）（填“正方形”或“长方形”），长是（    ）米，宽是（    ）米，周长是（    ）米

（3）在剩下的图形里再画一个最大的正方形，这个正方形的边长是（    ）米。

2.折一折，按步骤折出小盒子。折完后再打开，仔细观察折痕，你能不用尺子，求出盒子底部的周长是多少吗？（已知纸长14cm，宽11cm）课后可与同学讨论。

设计意图：本环节设计了一次课内练习和一次操作活动，抓住课堂重点练习，使学生在运用所学知识解决问题、巩固新知、提高动手操作能力的同时，经过自主思考，感受数学与生活的紧密结合。第2题是一道提升与拓展的题目，可以使有能力的学生进行更加深层次的思考。

（四）课堂小结

1.师：本节课你收获了什么？

2.课堂评价

设计意图：引导学生把学过的知识说出来，让学生说说这堂课的学习收获是什么，加深学生对数学的知识在折纸中、在生活中无处不在的认识，运用数学思维解题。

八、教学反思

数学的学习在生活中随处可见，环环相扣。一节积极、良好、快乐的课堂能够让学生获得知识与技能，也能让学生提起对数学学习的乐趣。本节课将数学学习与折纸活动结合，让学生在玩中学、学中玩。学生在这样的学习氛围中研究图形、几何知识在折纸活动中的应用，进一步促进其空间想像能力和动手创新能力，切实提高其思维水平，提升“融·乐”课堂的学习效果。

笔者设置了这样的授课活动：怎样在一张长方形的纸中折出一个最大的正方形。这样的题目对于小学三年级的学生来说还是比较抽象的，单单靠想像是比较困难的。因此，笔者在课堂上让学生自己练习、自己摸索、自己动手，把数学的学习兴趣调动起来，培养数学的思维。有个别学生不用对角折的方法，折出来的图形不是一个最大的正方形，甚至折出来的图形根本不是一个正方形。这时，笔者及时反问他：你用尺子量一量，看看你折出来的图形四条边都相等吗？想一想有没有其它方法可以保证你折出来的图形四条边都是相等的，四个角都是直角呢？这时学生就会有意识地联系正方形的特点，将知识通过折纸这个活动渗入到日常中运用。

折纸这项活动具有可塑性、创新性等特点，既能培养学生动手操作的能力，又能提高学生的想象力、创造力。本课堂还设置了另一个教学活动：用一张纸对边折一次、两次、三次……让学生数出折出的小图形的个数，求小图形的周长，然后观察这些数据，以此类推，找出其中的规律。并且猜测：一张纸如果足够大，可以无限对折下去吗？有的学生猜测：只要这张纸是无限大的，那么我们就可以一直叠下去。对于学生大胆的想法，笔者首先是大力表扬并且赞同他们，鼓励学生说出自己心里的想法，接着告诉他们这只是初步的猜测，在数学的学习当中我们必须用科学的方法来证实。此时，笔者再适时给学生观看几个知识小拓展，丰富他们的课外知识，引发学生的探究欲望。

九、板书设计

责任编辑    刘    勇