打开文本图片集

【摘要】本文以人教版初中数学九年级上册实验与探究“如何设计跑道”（以下简称“如何设计跑道”）为例，通过帮助学校新修的运动场设计200米比赛的超前起跑点引出问题，经过小组合作测量跑道长度，以及不同起跑点之间的距离，发现跑道设计的不足之处，目的是让学生通过动手操作、自主探究、合作交流等方式获得知识，让学生经历一个发现知识、探索知识、获得知识并解决生活问题的过程。通过自学国际田联400米标准跑道设计图，探究半圆式田径场中圆的半径、跑道宽度、弯道长度、直道长度等对确定超前起跑点的影响；通过跑道设计课，让学生成为小小设计师，发展和丰富学生的数学活动经验，促进学生的思考，培育学生的实践能力和创新意识。

【关键词】初中数学；项目式学习；小组合作；跑道设计

“如何设计跑道”属于中学数学的综合实践课。但其所需的数学知识并不复杂，学生可以提前学习。笔者围绕如何设计超前起跑点，让学生通过合作探究、手动测量、自主设计图纸等方式获得知识，提高学生合作学习、创新学习的能力。

一、立足生活，发现问题

《义务教育数学课程标准（2022年版）》指出，数学是研究数量关系和空间形式的科学。数学教学应该源于现实世界，并通过对研究对象的模型构建形成系统的结论和方法。数学不仅可以帮助学生认识客观世界，也能让学生通过数学经验的积累不断地发现现实世界的本质、关系和规律。新课标着重强调让学生从创设真实情境入手，而真实情境创设可以从社会生活、科学研究和学生已有数学经验等方面入手。教师在设计课程内容时尽可能地选择贴近学生生活经验、符合学生年龄特征和认知加工特点的素材。在新课标的指导下，我们的数学活动课程应该尽可能地贴近生活，立足校园活动，发现问题，解决问题。广东实验中学重新铺设了田径场，为本次项目式学习提供了生活背景。本课程以校运会田径比赛“200米比赛是否公平”为导向问题，以“测量和周长计算”为数学基础，以“自主设计半圆式田径场”为提升方向，学生通过数学知识和绘制设计图来解决问题。

二、合作学习，探究问题

综合实践领域的数学教学活动，以跨学科知识融合为为主题，以解决实际问题为方向，课堂内容以项目学习的方式呈现。学生通过综合运用数学和其它学科的知识与方法来解决真实的有意义的问题，从而获得创新意识、实践能力、社会担当等综合品质的提高。本次项目式学习通过样式迥异的跑道设计图让学生认识不同跑道的优劣势，比如，全程直跑道：在不考虑天气和磁场等因素下跑步比赛一定是公平的，但如果跑马拉松比赛或者长跑，则对场地长度的要求太高，不利于实现；山地跑道：对于跑步爱好者来说是大型森林氧吧，但山路曲折，很难保证比赛的公平性和可观赏性。由此可知，田径比赛中直道和弯道要结合，这样才可以既保证场地的实际功能，又可以保证比赛的公平性。通常情况下，由于田径场既要考虑田赛又要考虑径赛，所以一般为半圆式田径场。

学生通过合作学习《世界田联田径场地设施手册》，明确跑道设计过程中诸多因素所带来的影响。通过小组讨论，确定影响比赛公平性的因素为跑道长度。跑道长度是由直道长度和弯道长度组成，跑道中直道长度是不变的，而弯道长度的差异决定了总长度的差异。由于两侧的弯道组合起来恰好为圆形，则弯道长度恰好为圆的周长。而圆的周长取决于半径的长度，相邻跑道的半径之间都相差一个跑道宽度和一个分道宽度（设计图中用线段取代，可忽略宽度）。那么，我们就明确了跑道设计问题中的几个关键数据：直道长、第1道弯道半径、跑道宽度。

三、综合实践，科学论证

项目式学习教学涉及的问题主要是现实世界中具有开放性的问题。它并不是是非性很强的问题，而是如何用最优化的方法将现实问题转化为数学模型，进而解决问题。教师在其中就需要不断地引导学生提出合理假设、预测结果，选择合理的数学方法。当学生对数学模型表达条件与结果之间的关系有清晰的认识后，就能用真实情境检验模型、修正模型。本次跑道设计系列课程，为了保证科学性，我们在学校现有的跑道基础上进行精确测量，通过三人小组的合作，学会在测量工具有限的条件下，探究出怎样测量才能提升数据的准确度，怎样测量才可以在测量数据尽可能少的情况下得出结论。比如，如何选定基准线、如何处理数据，以及如何修正方案。（图1为测量活动，图2为学生讨论后的测量表）测量后，学生通过修正后的方案，学会设置提前起跑点，并由此来验证学校200米跑道中1、2、3、4道的设置是否合理。通过测量，发现2、3道之间的距离较大，得出3、4道选手参加比赛较为有利，从而得出在现有田径场的条件下跑道不公平的结论，并由此向学校提出跑道修正建议。

四、深度学习，学科融合

在设计跑道之前，学生自主探究和讨论了《世界田联田径场地设施手册》中关于400米标准半圆式田径场的设计规范。这类跨学科项目学习的趣味性和实用性更好，不仅可以为学生增添有趣味性的学习体验，还可以让学生通过提取信息，更加深度、集中地找到解决问题的方法，进而探索出最优设计方案。教师需要在这个过程中不断地鼓励学生独立思考、自主探索，提供开展协作的方案，让学生形成不惧失败的勇气。学科整合是学科间知识融合的过程，学科整合也是“深度学习”的一条路径。真正的数学不仅仅是数学课本里的知识整合，更应该是学科间的共同思考。因为数学源于生活，又服务于生活。在这个过程中学生慢慢感受到“触类旁通”的学科间知识整合过程。学生经过跨学科学习，深刻地明白一个400米跑道的标准田径场，如果直道长84.39米、跑道宽1.22米（跑道宽度可适当调整），那么各跑道如何设计起跑线才可以保证比赛公平、每条跑道应提前多少米。不仅200米跑道起跑点的画法与400米的起跑点不同，通常情况下为了保证比赛的公平性，起跑点设计在直跑道上而不选择在弯道上。通过自主学习，学生自主选择完成以下任务（三选一）：

1.请翻看学习资料，小组合作，自主设计一个400米半圆式田径场。

2.有一块空地长138米、宽69米，请利用这块空地设计一个半圆式田径场。

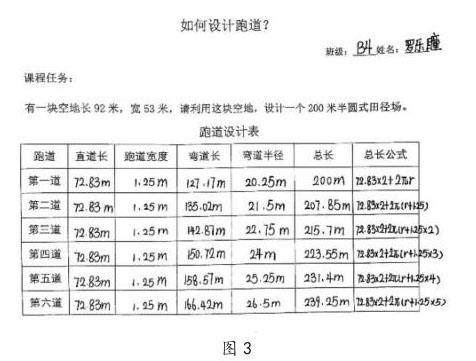
3.有一块空地长92米、宽53米，请利用这块空地，设计一个半圆式田径场。（图3、图4为学生自主完成的设计表和设计图）

五、善于挖掘，总结反思

该课程以设计跑道为活动素材，让学生通过学科融合学会计算超前起跑点，进一步加深对扇形弧长公式的认识和理解。学生在设计跑道的过程中，不断积累数学活动经验，并且学会解决此类问题的办法。通过实际操作，学生学会测量并明白如何测量使得数据又准确、又省时省力，并体会数学在实际生活中的应用，从而培养其主动参与学习活动的意识。在本次探究学习的过程中，我们还有一些需要解决的问题。比如，在实际生活中，除了比赛公平性问题之外，还有如何施工使得成本最低，也就是效益最大化问题；如何设计看台使得视野最佳；如何施工可以缩短工期等。这些问题都是我们可以继续挖掘的方向，也是数学教学中的一些基础问题。我们接下来的努力方向就是使这类课程系列化、背景丰富化、问题生活化以及解决方式多样化。

[本文系广州市教育研究院2021年度科研课题“双减背景下初中数学活动的校本课程研究”（课题编号：21BCZSX）研究成果]

参考文献：

[1]教育部.义务教育课程方案（2022年版）[S].北京师范大学出版社，2022.

[2]世界田径联合会，中国田径协会.世界田联田径场地设施手册[M].中国标准出版社，2022.

[3]国家市场监督管理总局，中国国家标准化管理委员会.中小学合成材料面层运动场地[EB/OL]. https：//std.samr.gov.cn/gb/search/gbDetailed？id=71F772D82C12D3A7E05397BE0A0AB82A.

责任编辑    陈    洋