打开文本图片集

【摘要】学校是教育的主阵地，“双减”政策政策实施后，目前课后作业设计已有不少的研究成果。基于此，本文探索改革传统教育教学模式的有效路径，以期构建“双减”政策下更加高效的课堂教学模式。数学建模可看作一种特殊的数学应用活动，侧重于构建新的数学模型去解决实际问题，倡导在启发式的教学活动中经历“选题—开题—做题—结题”的全过程，营造自主、合作、探究的学习方式，以期促进深度学习的真正发生。

【关键词】“双减”政策；小学数学；数学建模；课堂教学模式

2021年7月，中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》，意在构建高质量的教育体系，强化学校教育主阵地作用，有效减轻义务教育阶段学生过重作业负担和校外培训负担（以下简称“双减”政策）。政策实施后，目前课后作业设计已有不少的研究成果，如何在“双减”政策背景下深耕课堂，构建更加高效的课堂教学模式，让每一位学生接受适合的教育，成为了亟需探索的方向。

“数学建模是联系数学与应用的重要桥梁，是数学走向应用的必经之路。”为学生提供了大量参与数学实践与应用的机会。数学建模可看作一种特殊的数学应用活动，侧重于构建新的数学模型去解决实际问题。教育观念的革新指向学科核心素养的发展，数学建模活动以落实数学学科核心素养为依据，包括：符号意识、推理意识、模型意识、运算能力、数据意识、应用意识、创新意识。《义务数学教育课程标准（2022年版）》修订后，提出了“三会”的统领性目标，其中“会用数学的语言表达现实世界”为“数学建模”在基础教育数学课程中找准了位置。区别于传统的课堂教学模式，数学建模活动课倡导创建启发式的教学活动，营造自主、合作、探究的学习方式，以期促进深度学习的真正发生。

一、“双减”政策背景下的小学数学教学

（一）“双减”政策背景下小学教学教学现状

《义务数学教育课程标准（2022年版）》（以下简称《标准》）提出：“数学教育承载着落实立德树人根本任务、实施素质教育的功能。”小学数学无疑是基础教育中的重要内容，是培养学生数学思维、数学能力和数学品质的第一棒，服务于学生对数学的后续可持续性学习，当前的小学数学教学存在功利化、短视化教育的现状。

1.课堂教学模式固化

当前仍然有部分教师采取“讲授式”教学方法开展数学教学，课堂仅围绕着课本的数学知识和解题技能展开，于是有利于发展学生核心素养的探索过程被省略，一道道晦涩难懂的定理在课堂上“硬着陆”，导致学生未必知其所以然，学生抵触学习的心理也就是这样产生的。在这种急功近利的教学模式下，孩子获得了应试能力，却失去了终身学习的能力。

2.教学情境缺乏生活化

“双减”政策强调要让教育回归本真，小学的数学教育强调培养学生学以致用的能力，涵盖运用数学知识和技能去解决、分析实际问题的能力。在教学实践中，许多经久不衰的题目为了罗列出清晰的条件，情境往往都一笔带过，导致书本上的知识内容与实际生活割裂，学习无异于纸上谈兵。俞国娣老师强调：“未来孩子的竞争力不是单纯的解题，对孩子而言，最重要的不是掌握多少知识，而是自我学习的能力。”以知识为本位的时代已然过去，教师需要重新审视学生在课堂中应习得什么知识？需要学到什么水平？因此，教师要对教学方法进行处理，彰显数学课程的育人价值。

（二）数学建模为课堂注入“活水”

数学建模是数学应用的基本方式，是沟通数学与现实生活的桥梁。一个完整的数学建模过程包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、建立模型，确定参数、计算求解，验证结果、改进模型，最终解决实际问题。这一过程充分地反映了《标准》提出的核心素养构成，即会用数学的眼光观察现实世界、会用数学的思维思考现实世界和会用数学的语言表达现实世界。

传统的课堂教学模式是一种以老师为中心、书本为中心和课堂为中心的教学模式，与“双减”政策背景下倡导的高效课堂背道而驰。数学建模实践活动提供了一种更加高效的课堂教学模式，让我们在分数的背后看到了育人的方向。

1.教学形式创新

“封闭式”问题的求解过程往往是机械的、复制的、单向的，答案常常是固定和唯一的。而数学建模实践活动的开展打破束缚，起点是从实际生活中抽象出数学问题，从选题到结题都属于“开放式”，启发学生在课外调查、课中以小组的形式探讨等，以基础的数学知识辅助偏重实践的数学建模活动，相当于一个小型的科研过程，具有探究性、创新性和多样性的特征。在浓厚的探究氛围中，学生需要经历多次检验模型、完善并改进模型的过程，思维品质有显著提升。

2.优化教学内容

数学建模的的选题都是由学生的生活体验出发所提出来的生活实际问题，区别于课本理想化的数学问题情境，往往存在着有很多影响因素，建模活动需要学生分析出关键因素再对症下药，学生在探索过程中发展实践能力和应用能力。单运用某一册教材或某一学段所学的知识，难以到对复杂的现实问题做到对症下药，学生需利用不同学段所学知识综合解决问题，把旧知和新知的隔断墙打断，极大地锻炼了其分析问题、数学表征、解决问题等方面的能力，这些关键的数学能力的发展能够使学生自主地去获取、去探求、去寻觅、去掌握，并从中感受数学学习的乐趣，养成主动探索的习惯。

3.推行“合作探究式”学习模式

课堂布置学生独立思考问题，凸显了诊断的功能却忽略了个体的差异性，部分学生的能力不足以支撑其独自完成复杂的探究活动。《标准》指出：“教学活动应注重启发式，激发学生学习兴趣，引发学生积极思考，鼓励学生质疑问难。”俗话说：“三个臭皮匠，顶个诸葛亮。”鼓励“合作探究式”学习模式，体现出教学的层次性，有助于不同的学生在数学上得到不同的发展。在“合作探究式”作业完成过程中，不同能力层次的学生都能找到自己的定位，学生的内心更加放松，思维更加活跃，对于课堂知识各式各样的想法的交流能够有效培养学生的创新思维，让合作成为学生自主探究、大胆创新、发挥个性的舞台。

4.促进学科融合

《标准》在总目标中指出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系。”数学建模活动具有问题驱动、实践为主及多学科交叉应用三大特征，是培养数学应用创新型人才、促进跨学科交叉融合的重要途径。在数学建模活动中，学生以数学知识为基础，综合运用各学科知识解决来源于真实情境的问题，打破学科的壁垒，在促进师生跨学科交叉研究等方面发挥着其他教学活动无法替代的作用。

二、数学建模优化小学数学教学的策略

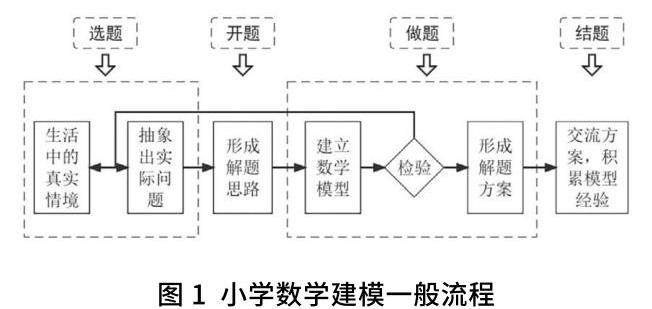
数学建模实践活动由四项基本要素组成：选题、开题、做题、结题。笔者主要以数学建模的四项基本要素为重心来分析如何优化小学数学教学的策略。

（一）选题——问题来源于真实情境

《标准》指出：“学生在真实情境中发现问题和提出问题，利用观察、猜测、实验、计算、推理、验证、数据分析、直观想象等方法分析问题和解决问题。”数学逻辑思维的形成离不开生活，数学建模活动课的教学内容和教学素材不必仿照课本内容，可以选取更贴近学生校园生活和家庭生活的教学素材，提升从实际情境中发现、提出问题的能力。

真实情境：新学期年级出现插班生，原花卉园设置的花盆数量不能满足五年级5个班学生的种植需求，而且花盆层层叠叠拿取不方便，因此需要根据学生数量重新购买花盆且确定花盆的摆放位置。

根据以上的真实情境，用简介的语言描述形成实际问题。

实际问题：如何根据学生数量重新合理购买花盆且确定花盆的摆放位置？

（二）开题——以探究式任务推动课堂

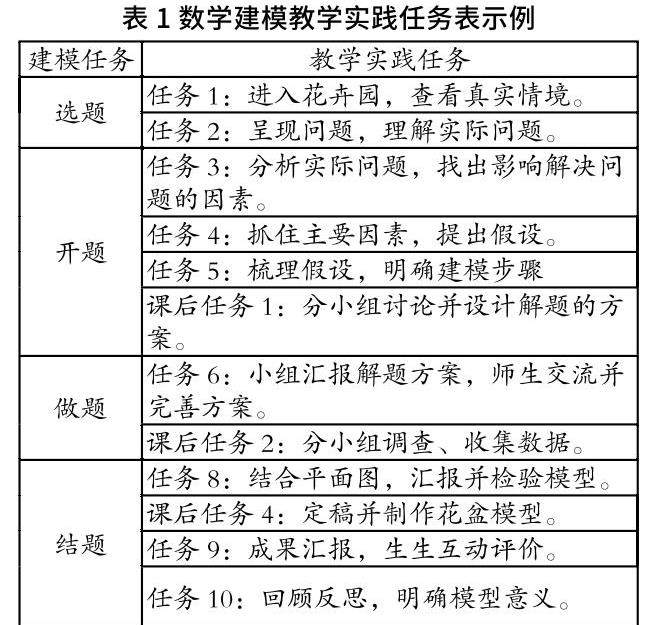
高质量的探究式任务在推动课堂的同时有助于激发学生的思维，提高学习主动性。数学建模的开题需要确定探究问题的方法以及任务，在小学阶段鼓励学生以文字点列或思维导图等形式理清解题思路。教师课上组织、引导学生互动交流，及时对学生的方案进行合理的评价，思考其可行性。紧接着根据每个教学模块设计相应的教学实践任务，再从数学的角度讨论问题的总体目标， 分析问题解决的具体任务、受哪些因素的影响，对目标的影响因素进行适当量化，最终给出解决问题的思路，并在此基础上，进一步提出新问题，引发学生深入思考。

（三）做题、结题——推行多元评价体系

多元化评价是指在评价学生的学习过程中，使用两种或两种以上的方式，对教学计划、学生学习状况和学科性质的综合评价。数学建模的过程性评价促进学生核心素养的发展，结果性评价更关注结题的质量。

1.过程性评价

学生是基于教学实践任务进行探索知识的，教师对建模过程中每一项实践任务都设置了相对应的可评价的标准，在检测学习效果的同时也促使学生对自身表现进行反思，强化了评价帮助学生有效调控学习过程的作用。过程性评价任务的形式各异，既可以是动笔解题、汇报交流等，关注知识的掌握程度；也可以是实践操作、考察迁移类推能力的活动等，关注学习能力的发展，但同时教师应关注到学生个体的差异性，分层设置评价任务。

2.结果性评价

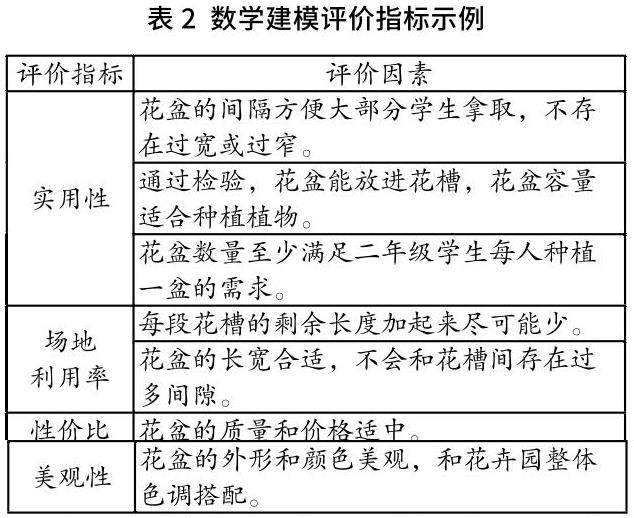
结果性评价帮助学生树立成果意识，学会反思改进，为将来再做类似工作有一个改进、发展的空间，同时开阔视野，感悟数学模型是可以解决很多问题的思想、方法、工具。评价因素的设置对应开题的影响因素，评价任务更具有针对性，做到“教—学—评”一致性。

教育是国家的立国之本，强国之基，“双减”政策的推进，让教师重新审视教学中存在的问题。数学建模活有助于构建高效课堂，是改革传统教育教学模式的有效路径，极大地提高师生的实践创新能力，实现课改和基础教育发展在更深层次上的突破。用发展的目光看待课堂教学，在研究中愈探愈出，愈研愈入，愈往而不知其所穷，正是我们教育工作者的职责所在。

参考文献：

[1]李大潜.从数学建模到问题驱动的应用数学[J].数学建模及其应用，2014，3（3）：1-9.

[2]范一斐.做“儿童友好型”家庭里的“智慧型家长”——“双减”政策下的家庭教育[J].杭州，2021（18）：66-67.

[3]中华人民共和国教育部.全日制义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[4]吴孟达，王丹，毛紫阳.面向问题的数学教学——谈数学建模对数学教学改革的启示[J]．高等教育研究学报，2011，34（S1）：15-16.

[5]韩玉敏．新课改背景下如何构建小学数学多元化评价体系[J].中国校外教育（旬刊），2016（10）：94-95.

特约编辑 杨 杰