打开文本图片集

【摘要】随着国家“双减”政策的深入落实，学生“说题”已成为一种新型教学模式，深受学生喜爱和欢迎。新课程标准明确指出，教师应当推动学生学习方式的转变，引导他们积极主动参与探究性学习。在新形势下，初中数学教师通过开展“说题”教学，不仅能够有效激发学生学习兴趣，提高数学语言表达的能力，还能促进学生核心素养发展，彰显数学课程的育人价值。本文就初中数学学生改如何说题进行了探析。

【关键词】初中数学；说题案例；说题能力；说题评价

《义务教育数学课程标准》（2022版）指出：数学教学要引导学生在发现问题、提出问题的同时，会用数学的眼光观察现实世界；在分析问题的同时，会用数学的思维思考现实世界；在用数学方法解决问题的过程中，会用数学的语言表达现实世界。应丰富教学方式，发挥每一种教学方式的育人价值，促进学生核心素养发展。

笔者近三年开展省级课题“教学倾听视觉下提高初中学生数学说题能力的策略研究”研究，带领团队开发了《初中数学学生说题指引》《初中数学学生说题评价指标》等，引导学生积极参与说题教学活动，有效促进学生的数学学习兴趣、学习自信和语言表达能力地提高，培养了学生分析问题和解决问题的能力，促进学生核心素养发展，彰显了数学课程的育人价值。下面以其中一个学生的说题案例进行阐析。

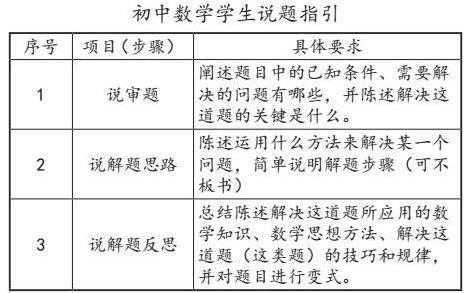
一 、根据《初中数学学生说题指引》来引导学生

二、《初中数学学生说题评价指标》

此说题评价指标从“审题、解题思路、反思”三个维度，A、B、C、D四个等级对学生的说题表现进行评价。评价主体包括说题学生本人自评、其他学生评价、教师评价。

三、学生说题案例

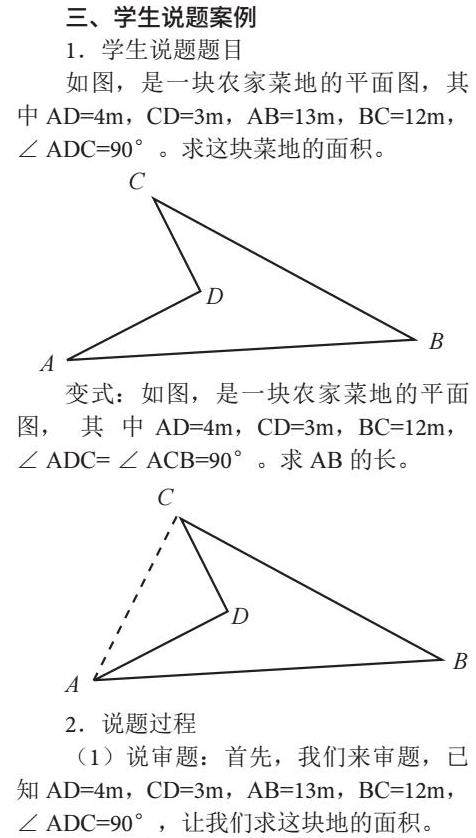
1．学生说题题目

如图，是一块农家菜地的平面图，其中AD=4m，CD=3m，AB=13m，BC=12m，∠ADC=90°。求这块菜地的面积。

变式：如图，是一块农家菜地的平面图，其中AD=4m，CD=3m，BC=12m，∠ADC=∠ACB=90°。求AB的长。

2．说题过程

（1）说审题：首先，我们来审题，已知AD=4m，CD=3m，AB=13m，BC=12m，∠ADC=90°，让我们求这块地的面积。

（2）说解题思路：我们看图可以看出这是一个不规则图形，我们不能直接用面积公式来求，需要转化为规则图形来求。这里我们尝试连接AC，进而得到两个三角形，分别是大的三角形ABC和小的三角形ADC，所以这块地的面积就等于大的三角形ABC的面积减小的三角形ADC的面积即。先看小的三角形ADC，已知两直角边，可以用勾股定理求斜边，再看大的三角形ABC，已知三边的长分别是5，12，13，是一组常见的勾股数，所以我们可以利用勾股定理的逆定理来证明这个三角形ABC是一个直角三角形，且直角为∠ACB，所以这两个三角形都是直角三角形，那么它们的面积就会等于两直角边乘积的一半。

（3）说反思：下面来总结一下，这道题主要考察了勾股定理及其逆定理的综合运用，我们在解这道题是运用割补思想将不规则图形转化为规则图形，进而求得面积，运用勾股定理求出直角三角形边的长，运用勾股定理的逆定理证明一个三角形是直角三角形，把求菜地的面积转化为求两个三角形的面积之差，所以这道题运用了割补思想和转化思想。

（4）说变式：接下来我们看变式，首先我们先审题，如图是一块农家菜地平面图，其中AD=4m，CD=3m，BC=12m，∠ADC=∠ACB=90°，让我们求AB的长。

3．说题点评

第一，其他学生点评。说题过程中语言流畅有条理，板书清晰；巧妙地将不规则图形转变为规则图形；清晰表达出解决问题的关键是作出辅助线；还能在原题的基础上加以变式，活学活用；将所学知识进行创新，可见对知识点掌握牢固。

第二，教师点评。该同学选了一道“勾股定理”的题目进行说题，说题过程完整，包含了说审题、说解题思路、说反思、说变式。在说解题思路的时候，善于分析“菜地”是一个不规则的图形，要想求它的面积需要转化为规则图形，而转化的方法就是巧妙添加辅助线，运用勾股定理求直角三角形的边，运用勾股定理的逆定理证明一个三角形是直角三角形，从而把求菜地的面积转化为求两个直角三角形的面积之差。在说反思的过程中，麦子茵同学不仅能清晰总结题目所考知识点，还能准确归纳数学思想方法，总结解题规律，最后还能灵活变式。整个说题过程思路清晰，表达流利，举止自信、大方，是一次比较高质量的说题。

建议在总结解题规律的时候再具体、详细一些，不仅能让自己，还能让听说题的同学能够更好地掌握这类题的解题技巧；同时，也希望变式更多样、更丰富，帮助大家发散思维。

四、案例说明与分析

1．案例说明

笔者及团队教师在课题实施过程中以上述的《初中数学学生说题指引》《初中数学学生说题评价指标》等研究工具为载体，分别通过课前说上一节课的作业、课中说例题习题、课后布置说题作业等形式组织学生说数学题。上述案例是笔者执教人教版初中数学第十七章《勾股定理》章复习后布置的课后说题作业，学生自主选题完成作业，说题展示课中学生面向全班同学和教师进行说题展示，其他学生进行评价，最后教师点评。

2．案例分析

章建跃博士指出：“数学教育应充分尊重学生在教学中的主体地位，给学生的数学学习以适度的指导，使学生提高对知识的领悟能力；培养学生用数学语言进行交流的能力，及良好的自我反省和自我调节的能力。”此案例突出了学生的主体地位，布置数学说题作业能够进一步体现和落实“双减”政策，学生自主选题体现了教师尊重学生的差异性。课堂上给予学生充分的时间和空间进行数学表达，学生通过说审题、说解题思路、说反思、说变式等过程，深入理解和认识了相关的数学原理，掌握了一道题甚至一类题的解题技巧，发展了学生分析问题和解决问题的能力。说题评价以“自评—他评—师评”体现教学评价的多元化。

数学说题教学关注了学生在数学教学中的主体地位，营造氛围让学生充分用数学语言进行交流，培养了学生解题反思的习惯。学生“说什么、怎么说、说得怎么样”，具有明确的工具可采用，希望能够给广大数学教师开展数学说题教学提供参考。

【本文系2021年度广东省教育研究院中小学数学教学研究专项课题“教学倾听视觉下提高初中学生数学说题能力的策略研究”（立项编号：GDJY-2011-M114）研究成果】

参考文献：

[1]中华人民共和国教育部．义务教育数学课程标准（2022年版）[S]．北京师范大学出版社，2022：4．

[2]章建跃．数学教育随想录[M]．杭州：浙江教育出版社，2017．