打开文本图片集

【摘要】在学习和生活中，我们发现新问题的解决都是建立在已有知识的基础上，进而产生对应的解决方法。也就是许多问题都可以通过已有的方法，即掌握通解通法，能有效地解决。因此，学生数学建模等数学学科核心素养的养成应该扎根在基础问题和基本方法中。教师在教学中带领学生剖析问题的本质，发展核心素养是必须重视的教学策略之一。本文基于基础问题和基本方法，对高中数学三角形解的个数问题进行探究，以培养学生解决问题的能力，培育学生的数学学科核心素养。

【关键词】高中数学；基本问题；基本方法；数学建模；三角形解的个数

一、引言

探究高中数学三角形解的个数，可将问题分为四类情形：1.知晓三角形两边长度及其夹角度数；2.三边长均为已知量；3.掌握任一边长与两个角度的大小；4.得知任意两边及一边对角的角度。回顾已学的三角形识别规则，可以确认前三种场景下皆有一个确定的解决方案；而在第四种情况中，则可能存在一解、两解或无解的情形。面对最后一种情境，学生可能由于其复杂性难以解题，或者可能直接应用正余弦定理进行运算，得出表面答案而忽略了对该问题核心的深入钻研与归纳，导致出现错误的结论。这种处理方式不仅妨碍了学生对问题实质的深入理解，还可能促使学生陷入被动背诵结论的学习模式。下面，笔者以自己教授的市级公开课《三角形解的个数的探究》教学片段为例，分享在确认基础问题和掌握基本技巧的前提下，如何运用数学建模方式来研究和思考三角形解的个数问题的处理方法。

二、案例片段呈现

（一）设疑——营造情境

例：△ABC中，内角A、B、C所对的边分别是a、b、c，已知a=2，b=2，A=60o，判断上述条件中三角形是否存在。若存在，则有几解？若不存在，请说明理由。

设计目的：通过提问促使学生进行观察，进而总结出三角形解的数量与所提供条件之间的关系。

（二）探究——指向课题

学生经过思考、小组讨论后，展示解决方法。

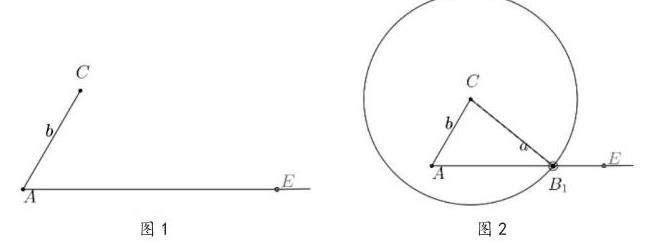
生1：鉴于掌握了∠A的度数及b边的长度，得以构造出图1。以C点为圆心，以2作为半径绘制一个圆弧，明确圆弧与AE射线相交于一点（见图2），故该三角形的解存在唯一解。

师：确定了三角形解的个数。那么如果我们改变a边的长度，或者改变∠A的大小，三角形解的个数会发生怎样的变化呢？

师生共同通过GeoGeBra软件进行探究，发现以下情况：

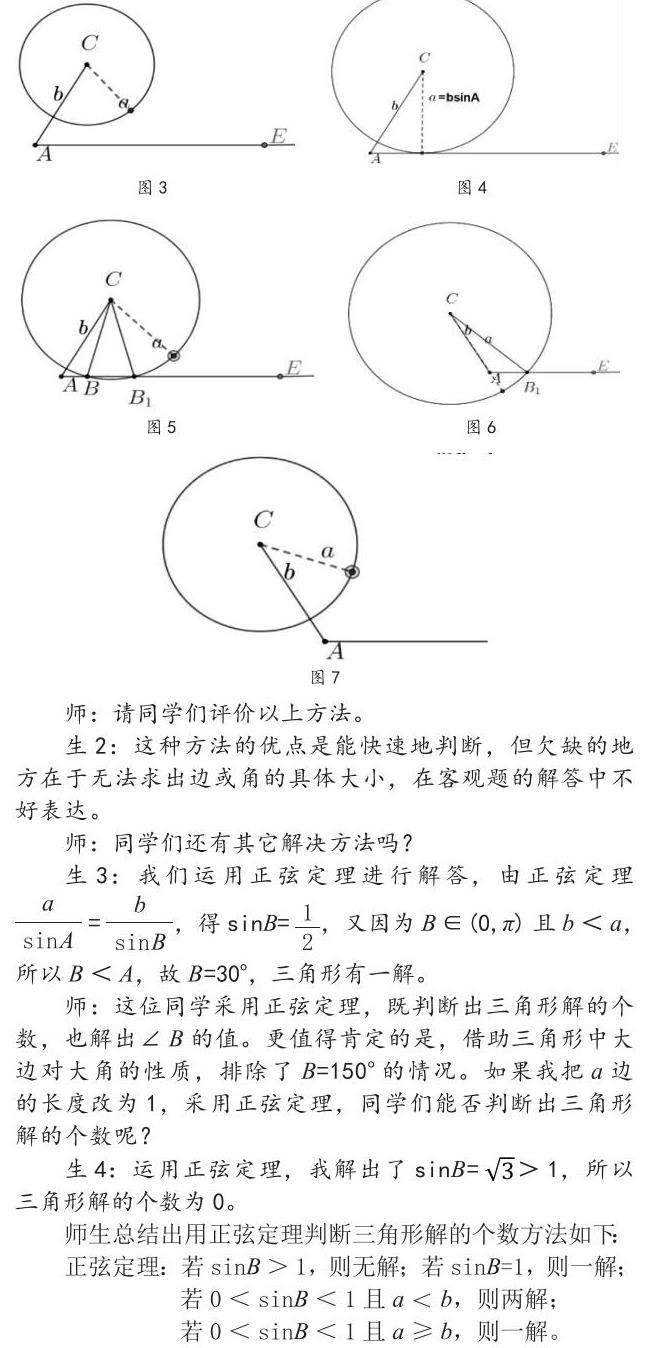
1.A为锐角。

若a＜bsinA，则无解；（如图3）

若a=bsinA或a≥b，则一解；（如图4、图2）

若bsinA＜a＜b，则两解。（如图5）

2.A为钝角或直角。

若a＞b，则一解；（如图6）

若a≤b，则无解。（如图7）

师：请同学们评价以上方法。

生2：这种方法的优点是能快速地判断，但欠缺的地方在于无法求出边或角的具体大小，在客观题的解答中不好表达。

师：同学们还有其它解决方法吗？

生3：我们运用正弦定理进行解答，由正弦定理=，得sinB=，又因为B∈（0，π）且b＜a，所以B＜A，故B=30o，三角形有一解。

师：这位同学采用正弦定理，既判断出三角形解的个数，也解出∠B的值。更值得肯定的是，借助三角形中大边对大角的性质，排除了B=150o的情况。如果我把a边的长度改为1，采用正弦定理，同学们能否判断出三角形解的个数呢？

生4：运用正弦定理，我解出了sinB=＞1，所以三角形解的个数为0。

师生总结出用正弦定理判断三角形解的个数方法如下：

正弦定理：若sinB＞1，则无解；若sinB=1，则一解；

若0＜sinB＜1且a＜b，则两解；

若0＜sinB＜1且a≥b，则一解。

生5：我是用余弦定理进行求解。由a2=c2+b2-2bccosA，得到c2-2c-8=0，解得c=4或c=-2（舍去），所以三角形有一解。

师：很好！我们用余弦定理也可以判断三角形解的个数，而且把第三边的长度也求出来了。那么请同学们思考，对于一般的情况，对于关于c的二次方程，我们是如何进一步判断三角形解的个数的？

生6：可以通过解方程来得知。

生7：老师，解出c边大小后是否需要检验三角形的三边是否满足两边之和大于第三边的性质？

师：这位同学提出了一个很好的问题。让我们一起来探究。由A∈（0，π），知cosA∈（-1，1），故-2bccosA∈（-2bc，2bc），可得c2+b2-2bccosA∈（c2+b2-2bc，c2+b2+2bc），即a2∈（（b-c）2，（b+c）2），所以a∈（|b-c|，b+c）。也就是说，对于关于c的二次方程，只要有正根，就一定满足三角形两边之和大于第三边的性质。那以后是不是可以直接通过判别式△的情况来判断三角形解的个数了？即△＞0则两解，△＜0则无解，△=0则一解。

生8：不行！万一出现了负根，我们是要舍去的！所以我们需要判断正根的个数。

师生共同总结余弦定理判断三角形解的个数的方法如下：

1.若△＜0，则无解；

2.若△≥0，则借助韦达定理判断所得的一元二次方程正根的个数：

（1）若两根之和大于零且两根之积大于零，则有两解；

（2）若两个之积小于零，则有一解；

（3）若两个之和小于零且两根之积大于零，则无解。

三、教学反思

本课是笔者基于基础问题和基本方法的教学理念，在数学建模核心素养的指导下，讲解《三角形解的个数的探究》时的一些处理方法。本课通过三种核心手法，指导学生深入探索问题解答的过程：1.作图并将问题转换为计算圆与射线的交点数量；2.应用正弦定理并转换为寻找函数交点的数量；3.利用余弦定理转换为求一元二次方程正实数解的数量。从教学结果来看，虽然这类问题对部分学生来说颇具挑战性，造成了一些困境，但经过授课，结合学生的课后反响，最终还是收获了相当积极的教学效果。它不仅加固了学生的基础理论知识，加强了他们对基础技能与方法的掌握，同时也使得学生领会到基本的数学思维。在此过程中，学生积累了宝贵的数学探索经验。

高中数学学习离不开解题环节，但在这个环节中解决问题的技艺尤为重要；立足于出题与评价的视角，我们更加需要深刻掌握数学的基本概念及其熟练应用。我们必须明白，数学题远不止于表面现象，背后蕴含着根本的数学思想。真正理解并能够灵巧运用这些思想，才是分析、解答各类数学问题，乃至深入探索数学领域的“基础”。因此，教师在教学过程中应当指引学生深入探究问题的核心及其解决路径。培育学生学会用数学的角度观察，使他们能以数学的方法去觉察或构筑问题，并运用数学逻辑去解析与应对问题；同时借助数学表达来阐述问题，从而在概括问题的过程中提炼出解决策略，并发展包含数学建模在内的数学学科核心素养。

参考文献：

[1]教育部.普通高中数学课程标准（2017年版 2020年修订）[S].人民教育出版社，2020.

[2]董彦波.转变学习方式，培养探究意识——一节关于三角形解的个数问题的探究式教学案例[J].数学教学通讯，2009（9）：20-21.

[3]钟启泉.深度学习[M].华东师范大学出版社，2021.

责任编辑    钟春雪