打开文本图片集

【摘要】“双减”政策明确指出：“发挥作业诊断、巩固、学情分析等功能”“鼓励布置分层、弹性和个性化作业，坚决克服机械、无效作业，杜绝重复性、惩罚性作业”。作业改革是基点，分层设计是突破点。本文基于SOLO分层理论，按照“反比例函数”单元知识点的不同思维层级确定作业目标，结合学生数学学习的思维进阶水平进行“三类四级进阶式”作业设计，为学生数学思维的进阶和差异性的发展提供有效的支撑，以期优化作业结构，构建科学有效的作业设计及评价模式，提高作业质量，帮助学生形成适合终身发展需要的数学核心素养。

【关键词】“双减”政策；SOLO分类理论；分层作业

一、SOLO分类理论概述

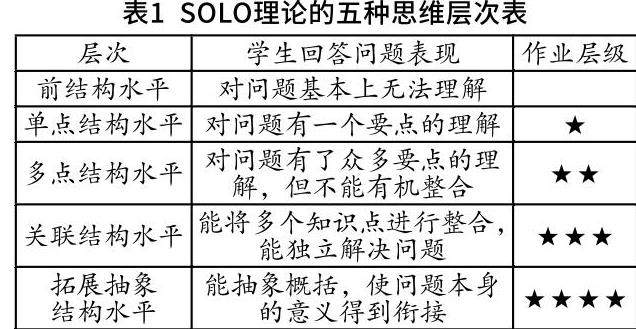
SOLO理论是一种“可观测的学习结果”分类理论，由香港大学心理学彼格斯教授及其同行经过实践研究总结而出，是一种质性评价方法，是对皮亚杰教育观点的一种补充与完善。SOLO理论根据学生对问题的答案来判断学生的思维层次与认知结构所处的阶段水平，将其分为五个认知结构层次，其思维层次结构框架如表1所示：

二、基于SOLO分类理论的“三类四级进阶式”作业的实施路径

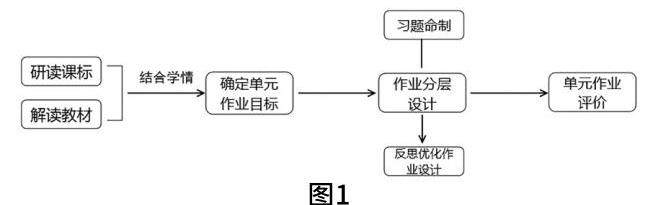
单元作业的质量对提升教育教学质量有着重要的影响，且通过单元作业设计还能提升教师对课程整体把控的能力。基于一线教学的实践，笔者总结出基于SOLO理论的单元作业设计路径图，如图1。

下面以人教版九下第二十六章“反比例函数”单元为载体，阐述基于SOLO理论对单元作业进行有效设计的实践与思考。

（一）基于课标解读教材，明确作业目标，理清思维层级

作业目标是作业设计的起点，SOLO分层理论下的作业设计要求教师要认真研读新课标和解读教材，从单元整体的视角去审视该单元知识之间的纵横联系，分析每个知识点所应达到的思维层级，明确哪些知识可以设计成单点结构、多点结构或者关联结构、抽象结构。因此，教师应基于新课标的学习要求、对教材的理解以及学生认知情况来确定单元作业目标。

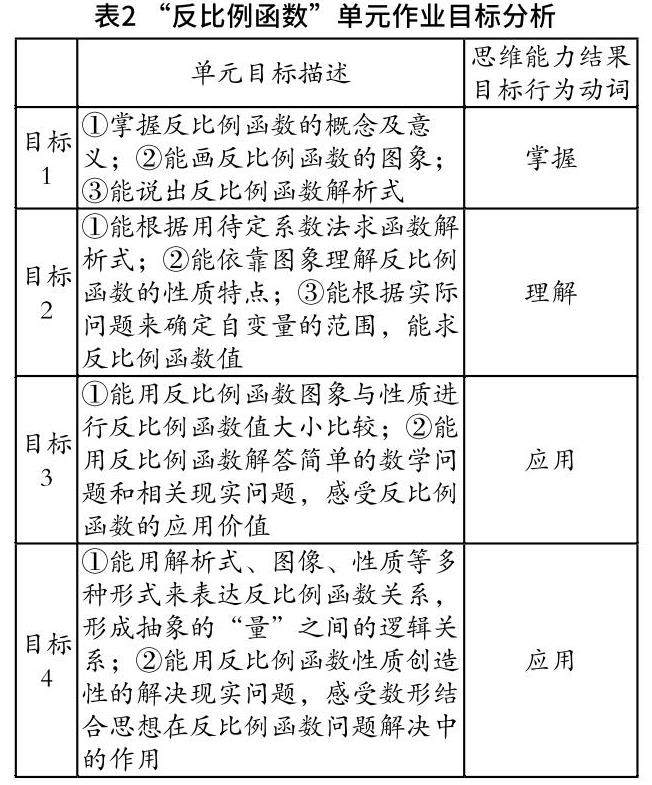
现以人教版九下第26章“反比例函数”单元为例，结合课程标准，将单元作业目标具化，基于SOLO分类理论的“反比例函数”单元作业目标对应的思维能力的结果目标如表2所示：

（二）基于单元作业目标分层设计，明晰思维进阶点

SOLO分类理论下的作业设计既要体现作业、教学、评价之间的关系，还要关注学生的基础和所处的认知水平，是基于教学目标和学情而设计的。因此在作业设计过程中，单元作业设计的核心是编制的作业内容，因此命题能力也非常重要。教师要根据确定的单元作业目标明晰学生在相关知识点的思维进阶点，进而设计出更为精准的“三类四级进阶式”作业。

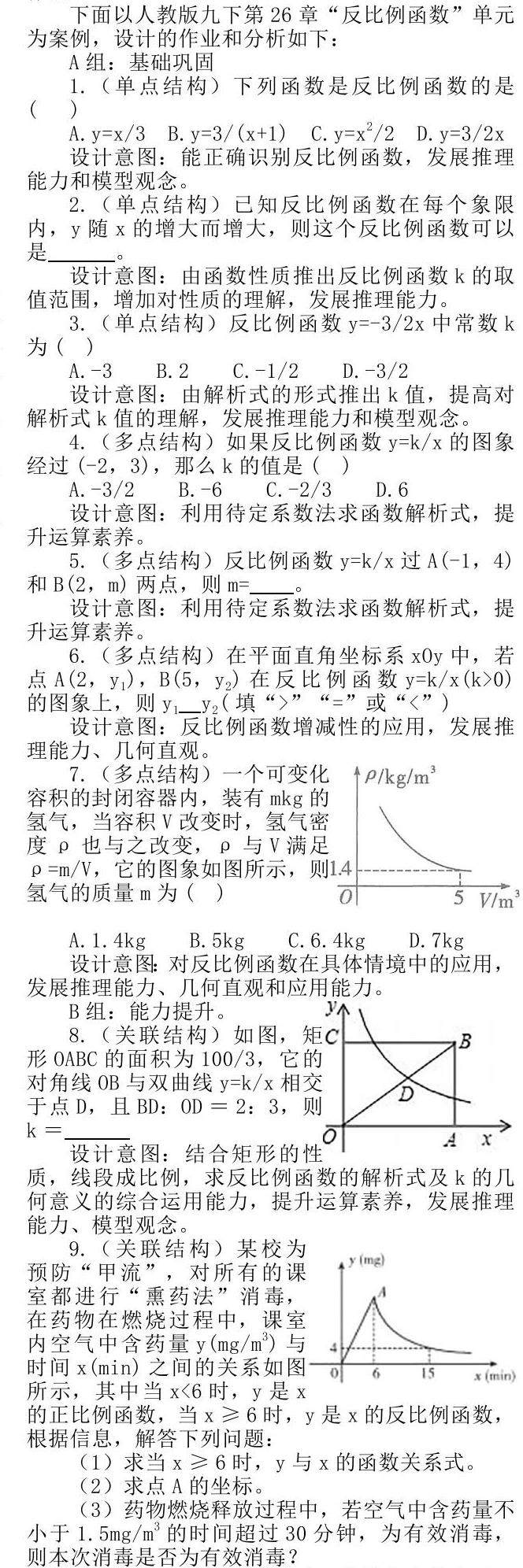
下面以人教版九下第26章“反比例函数”单元为案例，设计的作业和分析如下：

A组：基础巩固

1.（单点结构）下列函数是反比例函数的是（ ）

A.y=x/3 B.y=3/（x+1） C.y=x2/2 D.y=3/2x

设计意图：能正确识别反比例函数，发展推理能力和模型观念。

2.（单点结构）已知反比例函数在每个象限内，y随x的增大而增大，则这个反比例函数可以是 。

设计意图：由函数性质推出反比例函数k的取值范围，增加对性质的理解，发展推理能力。

3.（单点结构）反比例函数y=-3/2x中常数k为（ ）

A.-3 B.2 C.-1/2 D.-3/2

设计意图：由解析式的形式推出k值，提高对解析式k值的理解，发展推理能力和模型观念。

4.（多点结构）如果反比例函数y=k/x的图象经过（-2，3），那么k的值是（ ）

A.-3/2 B.-6 C.-2/3 D.6

设计意图：利用待定系数法求函数解析式，提升运算素养。

5.（多点结构）反比例函数y=k/x过A（-1，4）和B（2，m）两点，则m= 。

设计意图：利用待定系数法求函数解析式，提升运算素养。

6.（多点结构）在平面直角坐标系xOy中，若点A（2，y1），B（5，y2）在反比例函数y=k/x（k>0）的图象上，则y1 y2（填“>”“=”或“<”）

设计意图：反比例函数增减性的应用，发展推理能力、几何直观。

7.（多点结构）一个可变化容积的封闭容器内，装有mkg的氢气，当容积V改变时，氢气密度ρ也与之改变，ρ与V满足ρ=m/V，它的图象如图所示，则氢气的质量m为（ ）

A.1.4kg B.5kg C.6.4kg D.7kg

设计意图：对反比例函数在具体情境中的应用，发展推理能力、几何直观和应用能力。

B组：能力提升。

8.（关联结构）如图，矩形OABC的面积为100/3，它的对角线OB与双曲线y=k/x相交于点D，且BD：OD＝2：3，则k＝

设计意图：结合矩形的性质，线段成比例，求反比例函数的解析式及k的几何意义的综合运用能力，提升运算素养，发展推理能力、模型观念。

9.（关联结构）某校为预防“甲流”，对所有的课室都进行“熏药法”消毒，在药物在燃烧过程中，课室内空气中含药量y（mg/m3）与时间x（min）之间的关系如图所示，其中当x<6时，y是x的正比例函数，当x≥6时，y是x的反比例函数，根据信息，解答下列问题：

（1）求当x≥6时，y与x的函数关系式。

（2）求点A的坐标。

（3）药物燃烧释放过程中，若空气中含药量不小于1.5mg/m3的时间超过30分钟，为有效消毒，则本次消毒是否为有效消毒？

设计意图：反比例函数在生活化情境中的应用，深化反比例和正比例函数概念的理解，发展几何直观、推理能力及模型观念。

C组：拓展应用。

10.（抽象拓展结构）某超市在40天内试销一种成本为40元/件的新商品。在前19天，每天的销售单价都是80元/件；后21天改变了销售措施，规定“每天的销售单价m（元）由基础价格、浮动价格两部分构成，其中基础价格保持不变，浮动价格与x（第x天）成反比”。试销完毕后，通过统计整理还发现，试销售期间日销量n（件）是天数x（天）的一次函数，并且得到了如下表中的数据。

（1）求试销售期间日销量n（件）与x（天）的函数关系式。

（2）求后21天（20≤x≤40）每天的销售单价m（元）与x（天）的函数关系式。

（3）设第x天的利润为y元，则这40天中第几天获得的利润最大？最大利润是多少？

设计意图：反比例函数在生活化情境中的应用一次函数和反比例函数解决实际问题的能力，考察基础的同时也关注知识的横纵联结，进一步深化学生对函数概念的理解，发展推理能力及模型观念.

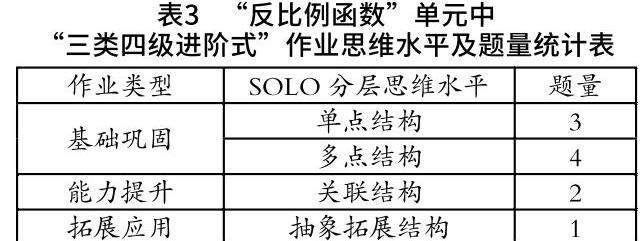
作业设计除了要关注目标、针对性、趣味性、层次性之外，还要兼顾学情，关注作业内容难度、完成时间、自主选择等问题。根据SOLO分类理论对作业题组进行思维结构分成三类四级，三类为基础巩固、能力提升和拓展应用，四级为单点结构、多点结构题、关联结构、抽象拓展结构，其中题量分布为3道单点结构题星级占比约14.4％、4道多点结构题星级占比约38％、2道关联结构题星级占比约28.6％、1道抽象拓展结构题占比19％，难易程度符合中考难易比6：3：1，使得作业成为具有个性化、创新性和弹性化的“因人而异、因材施教”的学习任务，使人人在数学上都能获得良好的数学教育。作业内容思维水平层次和题量如表3所示：

（三）优化作业评价，理实作业设计模式

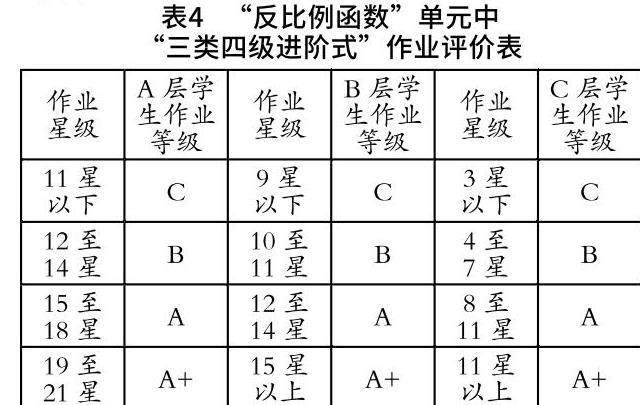
“三类四级进阶式”作业的宗旨并非是增加作业的类型，关键在于确保各层级作业的题目数量分配得当，确保学生完成每课时作业所需时间适宜，并在此基础上，通过作业的难度、种类和完成方式等多维角度，赋予学生一定的选择权，使得作业能够真正发挥培育学生数学核心素养的作用。以上案例的10道题中，有3道难度为★题，4道难度为★★题，2道难度为★★★题，1道难度为★★★★题，对于不同水平的学生应采用不同的评价标准，因此基于SOLO理论的作业设计既要对作业内容进行精选及分层，更要起到激励作用，让“起点低”的学生也能获得良好的评价，让“起点高”的学生也能适时进阶，“三类四级进阶式”作业评价表如表4所示。

三、基于SOLO理论，落实作业设计原则

（一）针对性原则

利用SOLO分类理论设计作业，要求教师以标为标、以本为本，精心选编、创编、整合作业内容。在选择作业内容时，要注重作业内容的针对性，深化学生对教学重、难点的掌握和理解，从而提高学生数学水平。如：第1题是针对“理解反比例函数概念”而设计的，第2题是针对“掌握反比例函数性质”而设计的。

（二）趣味性原则

作业需调动学生学习的积极性，基于SOLO理论的作业设计需关注作业的趣味性，通过生活场景化、跨学科融合等多样性的作业训练，让学生的数学核心素养得到进一步的发展。比如，第7题的物理问题，第9题在生活化情境中解决问题、第10题的销售问题，这些融合现实问题及跨学科问题的作业更有利于激发学生的学习欲，激发学生“三会”。

（三）分层设计原则

作业设计要根据学生的认知水平调整作业内容的难易度，根据中考难易度的6：3：1的原则，作业内容既要包含一定比例的基础性习题，帮助学生筑牢基础，也要满足题目之间、内容之间、学科之间应相互关联，将新旧知识交织成网状对学生进行测评，实现对学生数学核心素养的综合考查。如：“反比例函数”单元作业的设计难度由易到难逐步递进，满足不同层次水平的学生需求，内容分为基础巩固、能力提升、拓展应用三个部分，更是关联一次函数、矩形、相似等不同章节的内容，从而实现内容之间的网状融合，同时也融合了物理、化学和生活场景。只有这样，才能做到完全尊重差异性，使各层次的学生都能体会到学习的乐趣。

（四）分层评价原则

基于SOLO分类理论的作业应根据学生的差异性，采用不同评价标准，评价结果应及时反馈给学生，以便教师及时了解学生的学习情况和问题，并采取相应的措施进行改进作业设计，分层评价能有效调动不同层次学生完成作业的积极性，让不同的学生在数学学习上都能有有所收获，促进学生的数学核心素养的发展。

结语

“教也者，长善而救其失者也。”这是《学记·教之所由兴》中对教学的表述，这意味着教师应该根据学生的个体差异，给予适宜的指导和训练，作业既是连接课堂内外的纽带，更是提高教学质量的关键一环，以SOLO分类为理论依据，并结合教学实践，以提升学生思维为目标，开展“三类四级进阶式”作业设计。在实践中，教师还应建立激励机制，及时反馈，研判学生思维层级，依据作业情况及时反思教学，改进教学，从而实现作业服务于教学，促进学生的差异化发展，提升学生的数学核心素养，真正让“双减”政策落地。

【本文系珠海市教育研究院课题“基于SOLO理论下的初三数学作业设计及评价研究”（课题编号：2023ZHGHKT006）研究成果】

参考文献：

[1]何思，张彬，陈智豪，等.新课标背景下的大单元作业设计与实施探讨——基于“大单元作业”实验校案例与反馈[J].中国教师，2023（8）：72-76.

[2]邱娜玲，邱雅琴.基于SOLO分类理论的“分层进阶式”小学数学作业设计探究——以“多边形的面积”教学为例[J].中小学教学研究，2023，24（5）：17-21.

[3]黄炜.基于SOLO分类理论的“一次函数”单元作业设计[J].中学数学教学参考，2023（8）：60-63.

[4]刘洋洋.运用SOLO分类理论指导数学层次性教学[J].高中数学教与学，2022（10）：16-18，21.

[5]丁杭缨，许霜霜.单元视角下“四级进阶”式作业架构与实施[J].教学月刊小学版（数学），2022（3）：51-54.

[6]邓鲲.SOLO分类理论下“生活中的轴对称”单元作业设计[J].中学数学教学参考，2023（8）：57-60.

责任编辑 王苏燕