打开文本图片集

课题名称：提升小学教师学情调研与分析能力的策略研究；课题项目来源：北京教育学院2020年科研课题；课题编号：YB2020-13。

波利亚指出：“教师讲什么不重要，学生想什么比这重要一千倍！”学情调研和分析是教师展开教学设计和实施教学活动的起点。在实践中提高教师学情调研与分析的能力，可以更好地读懂学生的已有基础、学生的学习困难、学生的学习路径。

一、调研学生的已有基础

学生的已有基础是指调研学生学习新课之前，学生已经具备的知识基础、方法基础和经验基础。同时，这些基础应与新课内容密切相连，以圆的面积一课为例：

圆的面积属于“图形的认识与测量”主题下的内容，聚焦平面图形面积的测量，主要的课时包括面积、面积单位、长、正方形的面积、平行四边形、三角形、梯形的面积，它们共同的核心概念就是“面积单位的个数”，培育的核心素养主要体现在量感、推理意识、几何直观和空间观念。学生的学习历程主要分为以下几个阶段，虽然每个阶段的侧重不同，但是整体的教学目标是一以贯之的。

首先，在三年级的学习中留下用单位度量图形的基本方法。在此基础上，到了五年级又发展图形与图形之间的联系。我们可以看到学生在学习圆的面积以前主要积累了这两个方面的经验，同时，这两个方面的经验都源于对直边图形的测量。那么，到圆的面积又要发展什么？我想是化曲为直、有限与无限、近似和精确的极限思想，同时，直边积累的经验迁移到曲边。

二、把握学生的学习困难

学生在学习“圆的面积”之前，他们的已有基础是否像我们所想的那样？同时，他们在研究过程中，又会有怎样的学习困难？带着这样的思考我进行了如下的学情调研：“想办法测量这个圆的面积，把你的思考过程表达出来，如果遇到了困难也可以记录下来。”

调研反馈：

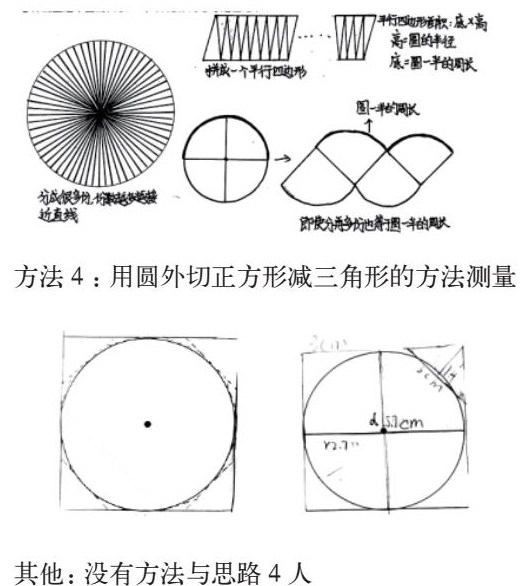
方法1：用小正方形测量

方法2：用三角形测量

方法3：用转化图形的方法测量

方法4：用圆外切正方形减三角形的方法测量

其他：没有方法与思路4人

通过对28名学生的调研结果进行整理，我们发现他们的个体思考主要体现在以下几个方面。通过对数据的整理有85.7%学生有办法测量，78.6%学生虽然有办法但依然带着困惑，14.3%学生无从下手。

那么，学生想到的办法真能解决这个问题吗？他们又遇到了怎样的困难？因此，可以通过进一步访谈了解学生的想法：

访谈1：在解决圆面积时最大的困难或问题是什么？

学生的困惑均来源于圆是一个曲边图形，边缘部分不好测量。

访谈2：你的方法很有创意，能说说你是怎么想到的吗？

21名学生能够结合已有学习经验表达自己的想法，3名学生在书中看到过将图形转化的方法。

情况分析：

解决圆面积问题，学生个体的思考方面：23名（82.1%）学生带着困惑，1名（3.6%）能够借助已有经验得到圆面积的计算方法，4名（14.3%）学生无从下手。

解决圆面积问题，学生所存在的困难方面：学生的困惑均来源于圆是一个曲边图形，边缘部分不好测量。

学生思考根源和有效经验方面：学生在学习面积、面积单位以及长方形和正方形的面积时，理解了面积的本质，掌握了用单位度量图形的基本方法；五年级学习平行四边形、梯形、三角形的面积时，借助方格纸学习图形面积，掌握了以上图形的面积的计算方法，同时能够建立图形与图形之间的联系，具备一定几何直观和推理意识。

三、规划学生的学习路径

回顾学生学习平面图形面积的历程，从面积到长方形正方形、再到平行四边形、梯形、三角形，学生经历一次从直边图形走向曲变图形的过程，这是学生要经历的一次思维飞跃。那么，在课堂中我们怎样帮助学生实现这次思维飞跃呢？

吴正宪老师主张：“坚守儿童立场。站在他们的角度去想问题、做事情。在课堂上不要和儿童争做“主角”，而是要充分的相信他们，开发他们的潜能，他们能自己做的事情教师不要包办代替，要让其在自主探索中培育自信和创新能力，促进儿童的自我成长。”因此，我想如果这个飞跃的过程是他们自己完成，那样才是真正有价值的。要将教师教的逻辑转化成学生学习的逻辑。那么，我应怎样实施的呢？

《圆的面积》教学片段：

生1：我们在学习面积时，用小方格的方法测量图形的面积，所以我想到了数圆里面有多少个小方格，它的面积就是多少。遇到的困难是边上空白的部分不知道面积是多少。

师：测量圆的面积为什么要用小方格呢？

生2：我们是拿小正方形当测量单位，再数图形中有多少个小正方格，就知道了圆的面积。

师：真好！原来我们以前就有了这样的经验，用单位测量图形的面积，看看图形中包含多少个面积单位，它的面积就是多少。

（板书：面积单位的个数）

师：在测量的过程中，你遇到了什么困难？看看同学们能不能帮你解决？

生1：在测量的过程中有一些剩余的部分，这些剩余的部分没有棱也没有角，没办法测量。

师：对呀！圆是一个曲边图形，剩下的部分怎么量呢？

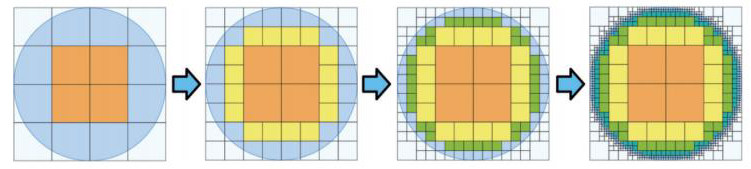
生2：我是要在圆里面取一个最大的正方形，然后在空白的部分再画一些小一点的正方形。我发现还有空白部分，于是再画一些更小的方格，让它无限接近圆。

师：你们觉得这样可以吗？为什么？

生3：我觉得可以，他的方法是求出最大的正方形以后，把空白的部分再画小正方形进行补充，再求出这些小正方形的面积，周而复始、越来越小，这样就能无限接近圆的面积。

师：真棒！刚才两位同学在测量时，一开始选择的单位比较大，遇到什么事儿了？

生齐：有不能测量的部分。

师：然后你们就想到什么了？

生齐：把单位化小。

师：如果还有空白呢？

生齐：那就再化小。

师：如果还有呢？

生齐：再化小，这样一直下去，就能无限接近圆的面积了。

通过案例呈现我们不难发现，本节课的教学实施主要经历以下几个过程：首先，是把问题抛出去，让学生带着问题和思考走进课堂；其次，组织学生交流测量方法，还原他们本真的思考；再次，不断引导学生发现问题和提出问题，分析和解决问题，从而感悟极限思想。通过学情调研的资源进行交流，改变教与学方式，引导学生在积极、主动的探究、学习过程中，学会想问题、做事情，从而真正落实核心素养的培育。