打开文本图片集

摘要：课程思政是我国高校思政理念的一种全新的模式，主要是在课堂上让学生学习知识的同时，接受思政教育，从而达到学校教书育人的目的。文章选取高等数学课程中极限模块，探索思政教育与高等数学课程融合的有效方法，实现高等数学课程的育人功能。

关键词：高等数学；课程思政；极限思想

引言

高等数学是高校理工类专业的公共基础必修课，是很多理工科专业课程的基础，其重要性是不言而喻的，高等数学课程内容主要包括一元函数微积分学、多元函数微积分学、微分方程、空间解析几何与无穷级数。在课程思想方面，高等数学课程的大多知识点有哲学的思想在里面，具有很大的启发性，并且许多数学家同时也都是哲学家，如牛顿、莱布尼茨等，也有很多重要的数学问题由哲学家提出，这些问题直接或者间接地推动了数学的发展。因此，高等数学与课程思政的融合的可操作性是非常强的。

一、极限与古代数学史

早在春秋战国时期，道家代表人物庄子在《庄子·天下篇》中记载：“一尺之锤，日取其半，万世不竭。”就反映了极限的思想，这是我国古代最早关于极限的思想论述，并且也提供了一个无穷小的例子，这一经典论断，在学习微积分的知识时，仍然会被反复提起。

古希腊人用“穷竭法”来研究求圆的面积问题，通过内接正多边形的面积来近似圆的面积：首先作圆内接四边形，接着增加边数，内接八边形、十六边形，依次类推，圆与多边形的面积会越来越接近，圆与多边形的差值越来越小，是为“穷竭”，这是一种比较粗糙的极限思想，因为没有办法保证“穷竭”之后的结果会是圆与多边形重合，但是这种思想却也反映了“无穷小”这一概念，即圆与多边形的差构成了“无穷小量”是在不断地趋于零。

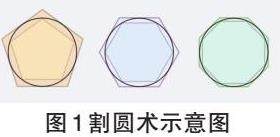
我国古代数学家刘徽在作《九章算术》时提出了“割圆术”这一方法：它在《九章算术》中指出：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”这一过程可以具体描述如下：从内接正六边形开始，逐渐增加边数至正九十六边形，甚至更多，如图1所示，随着边数的增加，正多边形的形状越来越接近圆的形状；随着边数趋向无穷大，内接正多边形的面积会与圆的面积越来越相似，最终在理论上等于圆面积。这句话表达了随着分割的越来越细，误差会越来越小，当分割无限细致时，误差可以忽略不计，就得到了圆的真实周长。刘徽的“割圆术”与古希腊计算圆面积所用的“穷竭法”思路是非常一致的，初步运用极限思想来解决生活中的一些实际问题。

在17世纪，牛顿与莱布尼茨在极限的基础上创立了微积分，就是，但当时人们对极限的严格定义还不是特别清楚，微积分的一些基本概念还是建立在物理与几何的基础上，具有很强的直观性与经验性，直到19世纪后期，德国数学家魏尔斯特拉给出数学上完整的极限的“[ε-δ]”定义，这才完善了微积分中的一些概念。

回顾极限的发展历史，经过了从静态到动态再到动态的发展过程，也从侧面反映了数学发展的辩证统一性，以极限的历史作为引例，引出极限的定义，可以让学生在掌握知识的同时感受到古代数学家对数学理论深刻的洞察力和创新能力，增加对数学文化和历史的了解。

二、极限与中国传统文化

三、结语

本文以极限为案例，探讨了如何有效地将课程思政与高等数学课程融合起来，思政元素的挖掘、融入实现课程思政的重要一步，需要做到显性与隐性结合，显隐结合就是将显性教育方式与隐性教育方式相结合，两者相辅相成，使高等数学课程与课程思政做到真正地深入融合。在课程思政的设计中，不仅要重视学生对知识技能的掌握，更要注重对学生人生价值观的塑造。绝非“一日之功”，需要有持之以恒的毅力，结合高等数学的学科特征，深入挖掘思政元素，有效地实现高等数学课程思政建设有机融合。

参考文献

[1]同济大学数学系.高等数学第七版[M].高等教育出版社，2014.

[2]陈宇.极限论的发展[J].邯郸大学学报，2000，（02）：11-12+48.

[3]贾光才.高职高等数学课堂教学有效性研究[J].科技创新导报，2020，17（09）：227-228.

[4]武丹.高等数学与课程思政的融合——以“导数及其应用”教学模块为例[J].辽宁省交通高等专科学校学报，2023，25（06）：76-79.

[5]何莎，冯颖，梁涛.高等数学课程思政教学案例设计研究[J].高等数学研究，2024，27（01）：95-98.

[6]夏文华，田智鲲，刘兰初，等.新工科背景下的高等数学课程思政方法[J].湖南工程学院学报（社会科学版），2023，33（04）：87-92.