打开文本图片集

摘要：针对运动控制系统中，具有复杂连接关系的被控对象，提出了一种基于微分方程矩阵的动力学建模方法，并通过解耦矩阵，实现逻辑轴到物理轴的完整闭环仿真。通过仿真模型进行动力学指标分析，应用灵敏度传递函数作为系统稳定性判据，搭建硬件控制平台，验证了该方法可以改善模型精度，提高了控制系统分析的有效性。

关键词：微分方程;动力学;控制系统;灵敏度

1.前言

控制系统的仿真分析与稳定性判定，是精密机构的核心研发环节，为实现多自由度逻辑轴的位置控制，需要采用多个物理机构耦合控制的方案。耦合控制的关键在于将某个自由度上的运动正确转化为多个物理机构的同步运动，即逻辑轴向物理轴的转化，在控制算法中设计解耦矩阵实现^[1]。为避免算法设计导致控制系统精度降低、稳定性下降等问题，需要进行仿真分析验证。被控对象一般由多个质量块连接而成，通过传递函数等方式建立的模型通常忽略连接关系而导致模型真实度降低，影响控制算法的仿真验证结果^[2]。

2.被控对象建模

在运动控制系统中，被控对象具有质量，弹性与刚性等动力学特征，通过有限元分析与传递函数建模实现仿真测试^[3]，但对于连接关系复杂的物理结构，传递函数很难体现不同质量块之间的作用方式，采用矩阵的形式进行不同关系之间的映射更加准确。

运动学微分方程如式（1）所示，具有质量，刚度，阻尼等特征。

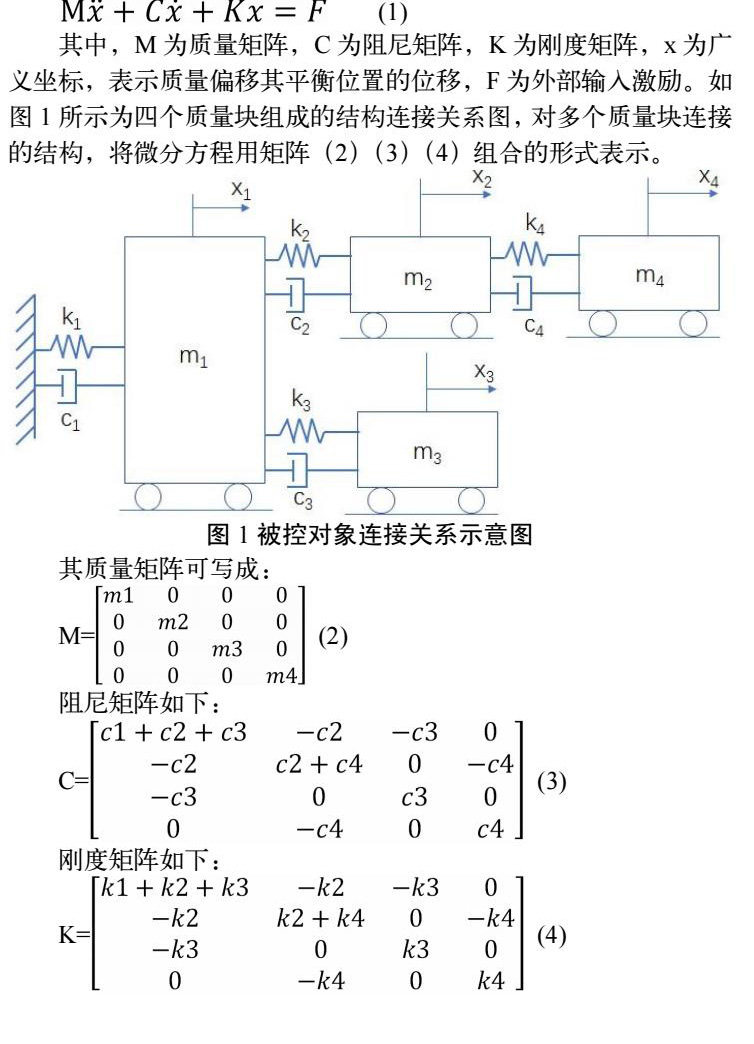
其中，M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，x为广义坐标，表示质量偏移其平衡位置的位移，F为外部输入激励。如图1所示为四个质量块组成的结构连接关系图，对多个质量块连接的结构，将微分方程用矩阵（2）（3）（4）组合的形式表示。

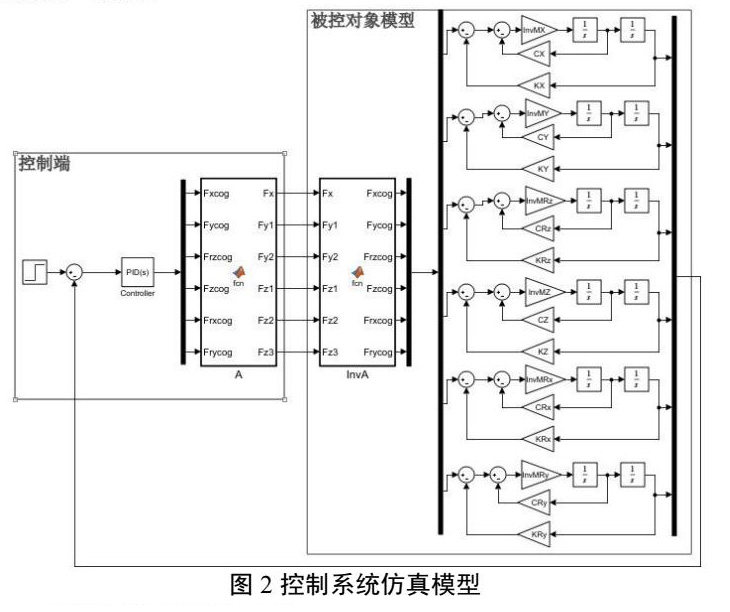
从矩阵形式可以看出，m1所代表的结构位移量x1受到来自c1，c2，c3阻尼力的影响，在矩阵对角线上体现;同时也会有反向阻尼力分别给到m2和m3所代表的结构，在矩阵非对角线上体现。刚度矩阵同理。可搭建仿真模型表征一个具有动力学特性的被控对象，将结构设计的参数输入到仿真模型中，可测得机械传递函数。在前端加入控制器，可测得开环传递函数。通过该方法可建立单一自由度的完整闭环控制系统。通常运动控制系统具有多个自由度的运动，对于一个质量块结构，假设坐标系原点为其重心，可以控制其围绕重心做X，Y，Rz，Z，Rx，Ry六个自由度的运动，每个自由度可建立独立的微分方程模型，进行动力学仿真分析。因此需要将控制系统进行解耦，拆分成多个单一自由度，在被控对象前端加入解耦矩阵，实现逻辑轴运动到物理机构的转化。定义解耦矩阵为A，完成了在多个自由度上的解耦，将其逆矩阵A^-1与六个自由度的微分方程串联，可以得到完整的被控对象模型。建立仿真模型架构如图2所示。

3.控制系统稳定性分析

稳定性是运动控制系统在闭环调试中最重要的指标，根据仿真模型，可对结构参数和控制算法进行验证。被控对象模型在不同自由度，由于参数不同，其动力学特性也有所差异，给定激励进行闭环调试，可在时域与频域进行仿真分析，时域可直接观测误差曲线是否收敛，频域可对系统稳定性进行判定。

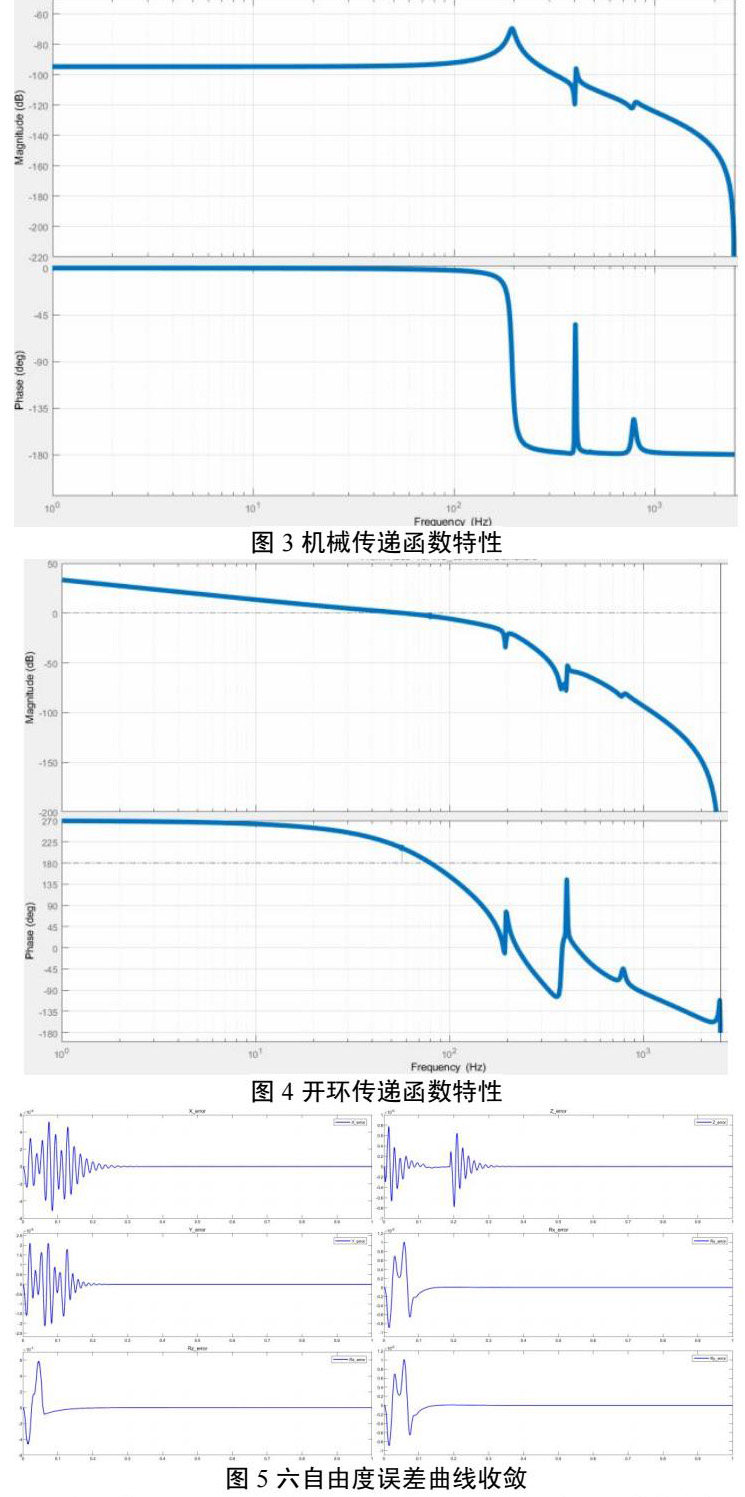
考虑到加工和装配的误差导致实际机构与三维模型具有一定差异时，需要进行迭代测试，在具备实际机构后，进行测试校准，以修正系统参数，满足离线优化算法的需求，同时可以进行动力学指标的灵敏度测试，从而判定控制系统稳定性，对后续结构设计修改提出指标需求。灵敏度测试是以闭环控制的参数调试为基准，首先固定被控对象的模型参数，进行控制算法仿真调试，测试分析机械传递函数，如图3所示，可以看出在110Hz和130Hz处有明显固有频率。

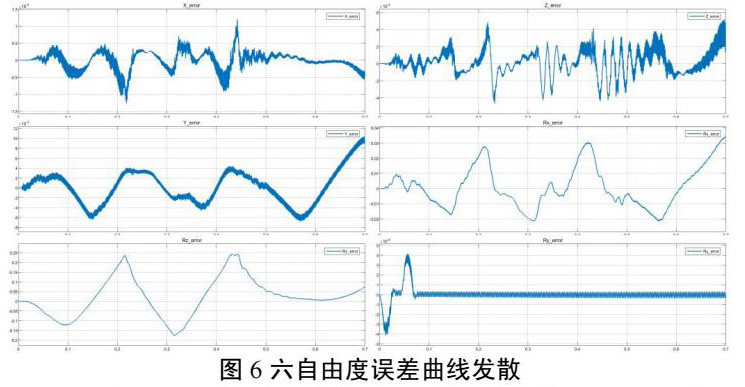
调节控制算法参数，对共振频率进行抑制并增加系统响应速度，得到稳定开环传递函数如图4所示，保证频域具有稳定带宽与相位裕度，给定六个自由度的激励输入，得到闭环误差曲线如图5所示，在时域上收敛可控。

在此基础上，保证控制算法不变，修改被控对象模型中的参数，进行动力学指标的灵敏度测试。根据机械振动公式（5），固有频率与刚度成正比。提高刚度参数，会增加结构的固有频率，有利于提高控制系统带宽。但是过高的刚度需求会带来结构设计的难度。因此在灵敏度仿真分析后，要提出合理的需求指标，保证在满足控制系统性能需求的前提下，尽可能减小结构设计风险。

对于刚度阻尼数据，在结构设计中主要体现在一阶模态，从而影响控制系统的频域性能，保证稳定裕度不变的前提下，增大或减小特定刚度阻尼参数，调节控制器直到满足系统时域与频域指标，得到临界稳定下的最小参数需求。如图6所示，当误差发散时，表示控制系统不稳定，此时结构的动力学参数不满足指标，需要提出约束条件，减少设计风险。

通过频域开环传递函数与时域误差曲线之间的关系，进一步将外部扰动与闭环误差之间的输入输出进行表示，在运动控制系统闭环中，s代表信号注入点，e代表闭环误差，将s作为输入，e作为输出计算传递函数，定义为灵敏度传递函数。在系统稳定时，绘制灵敏度传递函数伯德图，其在不同频率下的幅值增益均小于10db，表示系统在各个频率段稳定性均较好。调节控制器参数，增大系统带宽，减小稳定裕度，直到时域误差发散，此时绘制灵敏度传递函数伯德图，此时幅值增益在特定频率段接近20db，表示系统对该频率的灵敏度较高，存在不稳定风险。

针对控制仿真设计提出的动力学指标，需要与结构设计进行闭环验证，建立三点驱动的三维结构模型，如图7所示，对结构进行模态分析，其一阶固有频率在Rx自由度为120Hz，将参数加入到微分方程模型中仿真，带宽可调整到50Hz。

将三维模型加工制造，搭建硬件控制系统，采用相同的控制算法闭环调试，注入噪声得到系统的实际机械传递函数，其一阶模态在128Hz，将控制系统带宽调节至52Hz以下才具有良好的稳定裕度，此时灵敏度传递函数伯德图最大幅值增益小于15db，提高系统带宽至65Hz，此时灵敏度传递函数伯德图最大幅值增益为19db，时域误差增大，因此，绘制灵敏度传递函数的伯德图，根据其幅值增益的大小，判断控制系统稳定性是可行的。

4.结论

将具有多个质量块连接关系的被控对象，建立基于微分方程矩阵形式的动力学模型。并设计解耦矩阵，实现被控对象在六个自由度上的运动。搭建控制系统仿真调试，修改模型参数完成动力学指标分析，在此基础上，针对仿真结果，提出了一种将灵敏度传递函数作为系统稳定性分析方法，搭建硬件控制系统，测试验证了模型建立的真实性和系统稳定判据的可靠性。

参考文献

[1]彭珊.多自由度非线性振动系统的动力学研究[D].兰州交通大学，2014.

[2]杨天锡，丁雪梅等.多自由度伺服系统的非线性解耦控制[J].控制理论与应用，2011，28（8）1176-1180.

[3]武新峰，雷勇军等.基于有限元分析的复杂结构弹性振动传递函数建模[J].振动与冲击，2017，31（11）：57-61.