
- 收藏
- 加入书签
概率论与数理统计中贝叶斯公式的教学设计
摘要:贝叶斯公式是概率论与数理统计中重要的公式。本文采用研究式和启发式的教学方法推导讲解贝叶斯公式,培养学生严谨的科学态度和创造能力;通过贝叶斯公式在银行信用评价问题中的应用,培养学生提出问题、分析问题、解决问题的能力,勉励学生努力践行社会主义核心价值观,建立正确的人生观。
关键词:概率论与数理统计;贝叶斯公式;课程思政元素
本文以概率论与数理统计中“贝叶斯公式”这一节教学内容为例,从学情分析、教学目标、教学重难点和教学过程这四个方面设计教学模型,在教学实践中落实立德树人的根本任务。
一、学情分析
概率论与数理统计是高校理工类、经济管理类专业必学的一门公共课,它为学生今后的专业课学习提供必需的数学知识,同时培养学生的逻辑推理能力、以及用所学知识分析、解决实际问题的能力,全面提高学生的数学素养。贝叶斯公式是概率论与数理统计中一个重要的公式,它在大数据、人工智能、海难搜救、邮件过滤等问题中都有着重要的应用。
本节课授课对象为大二年级理工类、经济管理类学生,他们已经学习了高等数学的相关知识.他们的优势是有梦想、思维活跃, 容易接受新鲜事物, 但数学应用能力弱,尤其对纯数学概念的学习缺乏兴趣。应对措施:化繁为简、举例恰当、提高兴趣、增强自主学习能力。
二、教学目标
知识目标:让学生理解贝叶斯公式的形式和内容;掌握贝叶斯公式求概率的方法。
能力目标:使学生能够利用贝叶斯公式解决实际问题,进一步提高计算能力。
情感目标:提升学生分析解决问题的能力和自信心,提高学生的应用意识。
育人目标:注重学生中国梦, 社会主义核心价值观, 人文素质教育。
三、教学重难点
教学重点:应用贝叶斯公式计算概率。
教学难点:利用贝叶斯公式解决具体问题。
四、教学过程
(一)复习回顾
上节课,我们学习全概率公式时,通过这样一个例子:一个学生学习成绩好这个结果可能是由自身努力,教师教学水平高,学习习惯良好等等多种原因导致的。设事件A表示“学生学习成绩好”,事件B1为“学生自身努力”,事件B2为“教师教学水平高”,……,事件Bn为“学生学习习惯良好”,可以得到结果A发生的概率等于各个原因引起的概率的和,即全概率公式
上节课的学习,我们知道全概率公式体现了分类讨论、化繁为简的思想,是用来解决由因求果的问题。
教学设计:以生活实际案例“学生学习成绩问题”复习全概率公式,目的是减少课内回顾知识点所用的时间,充分突出重点;同时启发学生主动思考,提高学生的学习兴趣,为整堂课奠定良好的基础。
(二)课题引入
现在我们考虑问题的另一个角度:某学生学习成绩好这个结果发生了,问最有可能是哪种原因导致的呢?与全概率公式相比,这是一个逆向的过程,变成了由果求因的问题。这个问题应该怎样解决呢?
为了确定导致事件A发生的原因的概率,我们只需计算出此事件发生的条件下各个原因发生的可能性大小,即计算P(Bk|A),
我们把中间过程去掉,得到这个公式
就可以求出导致A发生的各个原因的概率这就是我们接下来介绍的贝叶斯公式。
(三)贝叶斯公式
定理 设S为样本空间,A是一个事件,B1,B2,……,Bn是S的一个划分,且P(A)>0,P(Bk)>0,(k=1,2,…,n),则
说明:(1)B1,B2,……,Bn是S的一个划分是为了保证公式中的条件概率有意义;(2)应用中,A表示某个结果,Bk看成导致这个结果发生的各种原因,故贝叶斯公式是用来解决由果求因的问题;(3)公式中的分子刚好是分母中的第k项,即A发生的条件下,第k个原因发生的可能性大小当然是第k个原因占总原因的比例。
贝叶斯公式实质为条件概率,在事件A发生的条件下,由这个试验结果实现对原因Bk的重新认识。按照先后顺序,我们称试验之前对Bk的认识为先验概率P(Bk),试验之后对Bk的认识为后验概率P(Bk|A)。
教学设计:采用启发式教学,引导学生构建贝叶斯公式,达到分散难点的目的,也培养了学生的创造力.通过三点补充说明,培养学生严谨的科学态度。贝叶斯公式最早是由英国数学家贝叶斯提出,时至今日,贝叶斯公式的思想已经发展成一整套统计推断的方法,在实际生活中具有广泛的应用。例如,大数据、人工智能、机器学习、海难搜救、邮件过滤、疾病诊断等等。
(四)银行信用评价问题
同学们,想一想通过观察试验会不会改变对原来事物的认识呢?
例 银行是如何评价小李的信用呢?
解 设事件A为“按期还款”,B为“小李守信”, 为“小李不守信”,则P(B)是银行认为小李守信的概率。假设先验概率 ,即银行最初对小李没有特别的认识,认为他守信,不守信的概率相同都是0.5,不失一般性, 假设参数
即守信的人有90%的可能性按期还款,不守信的人有50%的可能性按期还款。
由全概率公式
所以
小李通过一次按期还款,改变了银行对他的认识,由先验的守信概率0.5调整到了后验的守信概率0.64,确实通过按期还款改变了银行对他的认识。
如果小李再一次按期还款,银行是如何重新评估的呢?
注意,此时银行认为小李守信的概率已经不是最初的0.5了,而是变成了调整以后的0.64,不守信的概率只有0.36。再次按照贝叶斯公式计算,
通过又一次按期还款,信用评价再次得到提升。如果小李连续4次保持按期还款,经过计算,他的守信概率将由最初的0.5持续上升到0.91。但是如果出现逾期,信用也会相应的下降。这就是银行的信用评价模型。当然,实际中银行的模型可能更复杂,参数设置可能更合理,但核心思想就是贝叶斯公式。
教学设计:通过设计银行信用评价案例,用贝叶斯公式计算贷款人按期还款后银行对他的信用评价,并将先验概率和后验概率进行对比,揭示诚信的重要性。教育学生做人做事都要诚实守信,以陶行知名言“千教万教教人求真,千学万学学做真人”对学生进行诚信价值观的培育,勉励学生努力践行社会主义核心价值观。
(五)小结
(1)掌握贝叶斯公式的简单推导:由条件概率、乘法公式和全概率公式导出。
(2)把握贝叶斯公式的形式:公式两端事件的位置发生了逆转,称为逆概公式。
(3)学会贝叶斯公式的应用:用来解决由果求因的问题与全概率公式刚好相反。
(4)理解贝叶斯公式的本质:体现了利用样本信息纠正先验概率的思想。
思考题(伊索寓言“狼来了”)一个小孩每天到山上放羊, 山里有狼出没.第一天, 他在山上喊“狼来了!狼来了!”, 山下的村民闻声便去打狼, 发现狼没有来; 第二天仍是如此; 第三天, 狼真的来了, 可无论小孩怎么喊叫, 也没有人来救他, 因为前两次他说了谎, 人们不在相信他了。请计算小孩每次说谎后信誉度是如何下降的?
提示:设事件A表示“小孩撒谎”,事件B表示“小孩可信”,不妨假设过去村民对小孩的信任程度为P(B)=0.8,P( )=0.2,可信的孩子说谎的可能性为P(A|B)=0.1,不可信的孩子说谎的可能性为P( |B)=0.5。
教学设计:通过小结帮助学生更好地理解掌握贝叶斯公式;思考题继续深化知识,提升学生实践应用能力。再次诚信的重要性,勉励学生努力践行社会主义核心价值观。
五、结语
同学们,通过这节课的学习,贝叶斯公式中先验概率是基础,样本信息是关键,由此才能预见后验概率。同学们在学习和生活中要善于总结过去,牢牢把握现在,这样才能创造更美好的未来。
参考文献:
[1]李晨,陈丽萍.概率论与数理统计课程教学中思政元素的挖掘与实践[J].大学教育,2021(9):104-106.
[2]彭丹,刘东海. 关于概率论与数理统计课程思政的探索--基于数学文化的角度[J].当代教育理论与实践,2021(9),13(5):7-12.
[3]盛骥,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2019.
基金项目:
2020年河南省首批本科高校课程思政教学团队“河南工学院概率论与数理统计课程思政教学团队”。
2021年河南省首批职业教育与继续教育课程思政示范课程“河南工学院概率论与数理统计课程”.
作者简介:
张宁(1988.6-),女,汉族,河南杞县人,博士研究生,讲师,主要从事微分几何研究,概率论与数理统计教学。





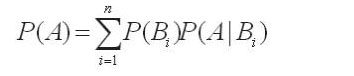



 京公网安备 11011302003690号
京公网安备 11011302003690号


