
- 收藏
- 加入书签
基于拔尖人才培养的初中数学项目式作业设计案例及评析
摘 要:初中数学作为基础教育的重要学科,对于培养学生的逻辑思维和创新能力具有重要作用。然而,传统的数学作业往往只注重知识的巩固及熟练,而忽略了学生实践能力和创新思维的培养。因此,我们设计初中数学项目式作业,旨在通过项目实践的方式,提高学生的实践能力和创新思维,为培养拔尖人才打下基础。
关键词:拔尖人才;初中数学;项目式作业
基于初中数学拔尖创新人才的培养,设计项目式学习的创新作业,通过设计具有挑战性和启发性的问题,引导学生进行深入思考和探索,从而培养他们的创新思维和解决问题的能力。
一、初中数学项目式作业
(一)初中数学项目式作业的含义
项目式学习作为一种以解决真实问题为本质的育人和学习方式旨在培养学生的创新精神和实践能力。选择实际问题情境作为项目式作业的素材进行设计,学生也能够通过完成作业获得分析问题和解决问题的体验,积累基本活动经验,运用数学与其他相关学科的知识,综合地、有逻辑地分析问题,经历分工合作、试验调查、建立模型、计算反思、解决问题的过程,提升思维能力,逐步形成“会用数学的思维思考现实世界”的核心素养。因此,开展项目式作业实践有助于初中数学拔尖人才的培养。
(二)初中数学项目式作业的设计流程
根据初中数学中数与代数、图形与几何、统计与概率三大领域的内容主线,在综合与实践领域的活动主题中挖掘教学内容的核心素养要素,通过寻找贴近学生的生活、学生感兴趣的内容设计实践型作业,由浅入深地发展学生数学核心素养,使数学学习内容与核心素养紧密地融合在一起。
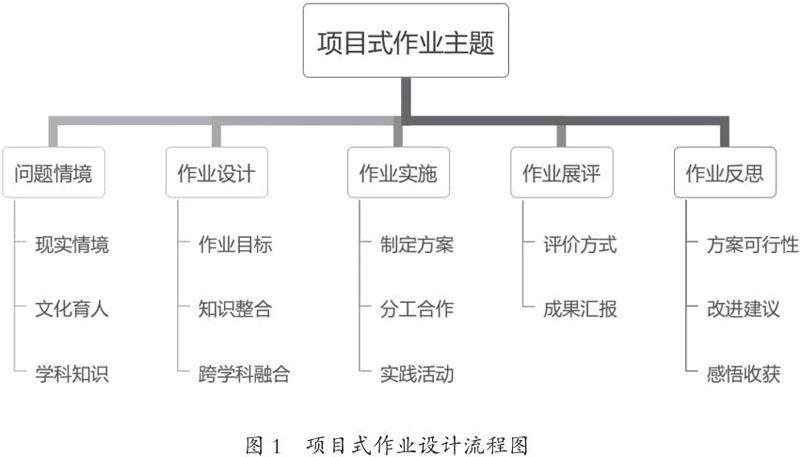
初中数学项目式作业设计流程主要包括以下五个步骤(如图1):
二、初中数学项目式作业设计案例
(一)作业内容
本次作业设计基于新课标的理念,为培养全面发展的学生,进行了跨学科融合,依托北师大版九年级上册第四章第六节利用相似三角形测高为作业知识支撑点,展开本次的实践作业。
项目式作业主题:了解顺峰山公园的旅游价值。
项目1:顺德是一座依水而兴、因水而美的城市,作为顺德“新十景”之一的顺峰山公园,以其独特的景观和丰富的文化内涵,吸引了无数游客前来探访。公园的入口处有巨型的牌坊,气势雄伟。请你查阅有关资料,为顺峰山公园写一段200字左右的景点介绍。
项目2:顺峰山公园入口处的巨型牌坊有多高?你有什么方法可以测量出牌坊的高度?请查阅有关资料或参考教材的例题、习题中的测量方案,利用已掌握的数学知识,制定测量顺峰山公园牌坊高度的方案,并对顺峰山公园牌坊的高度进行测量。
项目3:请整理项目2中的测量方案,为学校科技节设计数学活动成果展板或写成一篇数学小论文。
项目4:你喜欢到顺峰山公园游玩吗?请设计适合的调查问卷,开展实地调查,了解人们选择顺峰山公园游玩的理由以及对景点的建议,形成调查报告,以便更好地发挥顺峰山公园的旅游价值。
(二)作业效果
本次作业融合语文、数学、物理、地理等学科知识的综合运用,作业效果聚焦数学知识的综合运用与展示,通过项目1,让学生查阅资料,自主学习,撰写“家乡的顺峰山公园”“亚洲第一牌坊”等介绍,融合语文知识,既了解顺峰山公园的旅游价值,也增强家乡的自豪感;通过项目3设计的“亚洲第一牌坊与数学”“打卡亚洲第一牌坊”等展板或“顺峰山公园牌坊中的数学”等小论文,将项目式作业的成果显性化。项目4让学生经历实地调查,收集数据、整理数据、分析数据,并形成可行性的建议。
本作业聚焦项目2中的数学知识,同学们通过查阅资料找到了有关估算物体高度的不同方法,如泰勒斯测量金字塔高度的方法,利用阳光下的影子进行测量,利用标杆进行测量,利用镜子反射原理进行测量,利用了改变测量的角度大小以及测量前后两者之间的距离,还可以利用特殊角(30°,45°,60°)的三角板,以及后续的三角函数的知识计算出牌坊的高度等方法。经过总结对比,形成下列方案。
1.构造相似三角形
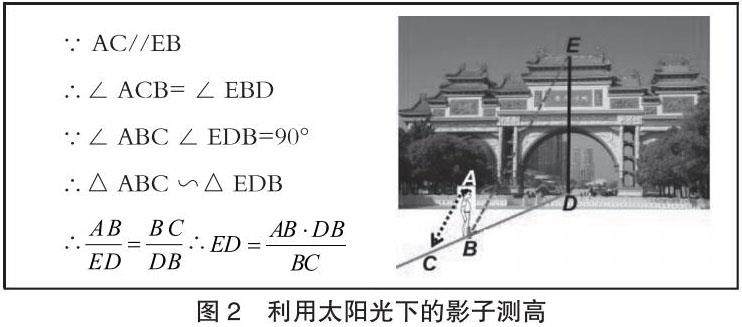
方案1利用太阳光下的影子(如图2):一名同学直立于顺峰山公园牌坊影子的顶端处,第二名同学测量该同学的身高(AB)和影长(BC),其余同学测量同一时刻顺峰山公园牌坊的影长(BD).利用△ABC∽△EDB,可求出顺峰山公园牌坊DE的高度。
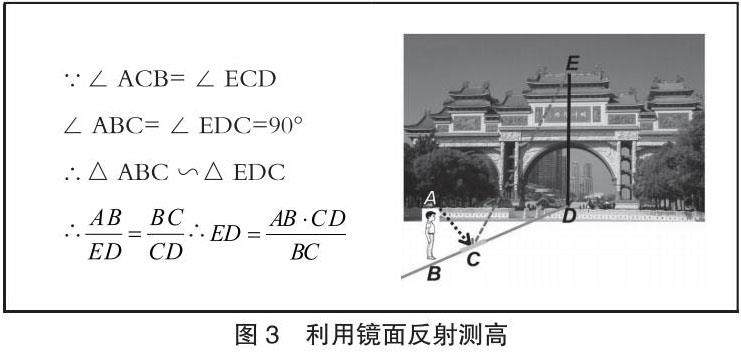
方案2利用镜面反射(图3)
由于影子形成需要一定天气和场所条件,可能会因为阴天影子不明显,或者顺峰山公园牌坊的影子太长,出现不便于测量的情况,此时可以使用镜面反射来测量顺峰山公园牌坊高度,增加实践作业的可行性。结合物理中学生所学“光在均匀介质中是沿直线传播的”和“镜面反射”知识,在顺峰山公园牌坊(DE)的一侧水平放置一面小平面镜C,调整至适当位置,使站在平面镜右侧的观测者能通过平面镜看到顺峰山公园牌坊的顶端,分别量出小平面镜到顺峰山公园牌坊(DC)和观测者(BC)的距离,由于观测者的高度已知,利用△ABC∽△EDC可求出顺峰山公园牌坊ED的高度。
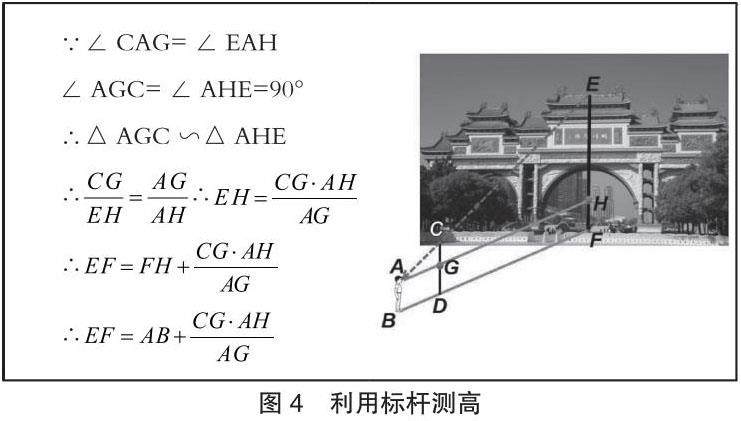
方案3.利用标杆进行测量(如图4)
在人与顺峰山公园牌坊中间垂直放置一根标杆,人前后移动使得人眼从标杆顶部正好看到顺峰山公园牌坊顶部,即人的眼睛A、标杆顶C、顺峰山公园牌坊顶E三点共线。分别量出人眼睛的高度AB、标杆高度CD、人与标杆距离BD、标杆与顺峰山公园牌坊距离DF,利用△AGC∽△AHE,可求出顺峰山公园牌坊EF的高度。
2.利用三角函数的知识
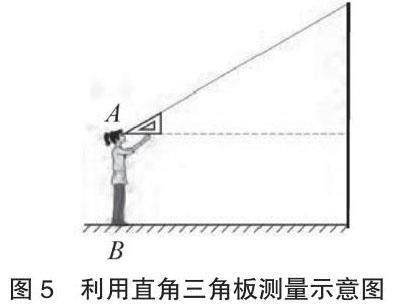
方案4.利用直角三角板的特殊角度(图5)
如图,人站在点B处拿一个30°角的直角三角板,人的眼睛A沿着直角三角板的斜边看到顺峰山公园牌坊顶C,构建出Rt∆AEC,测量出人到牌坊底的距离BD,再测量出人眼A与地面B之间的距离AB,则可以算出顺峰山公园牌坊CD的高度,
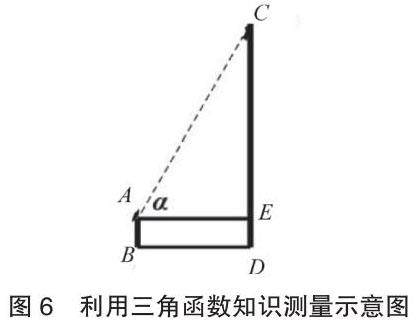
借助九下课本P22的方法,如图6,人站在牌坊前的点B处,利用测角仪测出观察牌坊顶C时的仰角α的度数,构建出Rt∆AEC,则,此时BD=AE.,再测量出人眼A与地面B之间的距离AB,以及人到牌坊的距离BD,则可以求出牌坊CD的高度为
方案6.通过测角仪进行两次测量
(三)作业评价
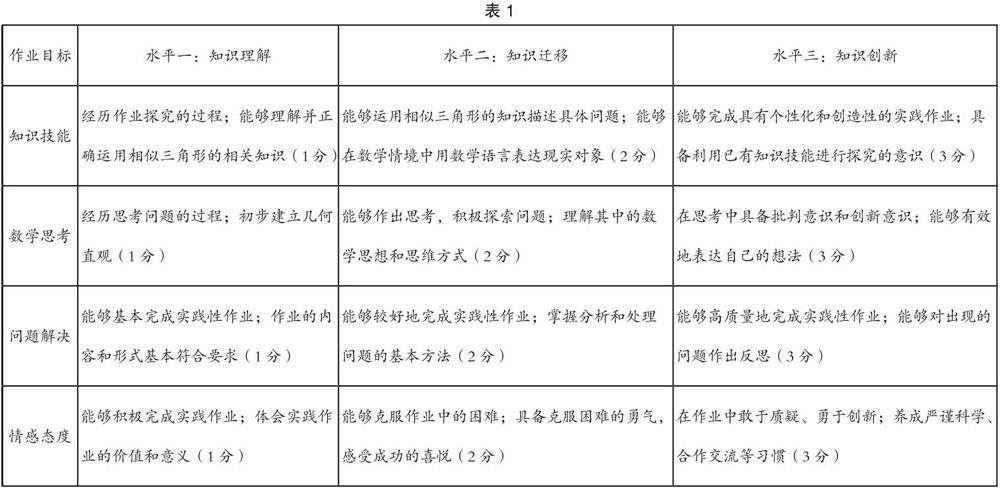
本作业评价定量标准可以参考表1。
三、项目式作业设计案例评析
《义务教育数学课程标准(2022年版)》倡导在综合与实践领域进行项目式学习,强调让学生经历发现问题→提出问题→分析问题→解决问题的过程。让学生在研究的过程中发现问题,并将其正确地转化为数学问题,从而构建数学模型,综合运用数学以及其他学科的知识与方法解决问题。通过项目式学习,培养学生问题解决能力,在实践中学会数学探究。
本案例融合语文、数学、物理、地理等学科知识的综合运用,聚焦解决问题中的数学知识,通过选取学生的身边情境,让学生了解顺峰山公园的旅游价值,测量顺峰山公园牌坊的高度,培养会用数学的眼光观察现实世界,在分析解决问题过程中,充分体现知识的综合运用。同时基于拔尖创新人才的培养,学生可以通过阅读、查阅相关资料,自主学习后续的知识(三角函数的知识),从特殊的30°到方案5、方案6中的一般的角度,体会从特殊到一般的思想,并能根据实际情况选择最优方案,培养用数学的思维思考现实世界。
参考文献:
[1]中华人民共和国教育部制定.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2]霍锐泉.应时势之变,创作业之新—“双减”政策下初中数学创新作业探究[J].中学数学研究,2023(6):3-7.
[3]刘智欢等.初中数学跨学科项目式作业设计的理念与路径[J].中小学课堂教学研究,2023(10):16-18.
[4]胡素芬.初中数学项目实践型作业的价值、困境与突破[J].中小学教师培训,2023(7):54-59.





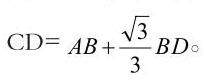


 京公网安备 11011302003690号
京公网安备 11011302003690号


