打开文本图片集

摘 要：文章以深证成指自2014年至2024年十年的大盘收盘指数的日收益率为研究对象进行研究。首先检验发现深证成指日收益率的时间序列是平稳的，偏度系数为负，说明数据是左偏的，峰度系数较大，显示了数据的尖峰厚尾的特征，因此考虑对序列拟合GARCH和EGARCH模型，研究发现深证成指具有显著的波动性和非对称性特点。以实证分析结果为依据，文章将从社会国家、资本市场、企业以及投资者四个维度，分别提出具有针对性的政策建议。

关键词：深证成指；GARCH族模型；对数收益率；波动性；

1 引言

金融市场波动性一直是投资者、学者和监管机构关注的焦点。深证成指作为中国股市的重要指标，其波动性对于理解市场风险、制定投资策略具有重要意义。传统的计量经济学模型通常假设时间序列的方差是恒定的，但这并不符合金融市场的实际情况。因此，文章采用GARCH模型，该模型能够刻画时间序列变量的条件异方差性，从而更好地分析和预测股市波动性。金融市场的波动性研究始于20世纪80年代，随着金融市场的不断发展和全球化进程的加速，市场波动性日益成为投资者和监管机构关注的重点。特别是1987年的全球股灾和2008年的金融危机，更是让人们深刻认识到波动性在市场风险管理中的重要性。

GARCH族模型自提出以来，在金融时间序列分析领域得到了广泛应用。这类模型能够有效地捕捉金融数据的尖峰厚尾特性、波动集聚性以及非对称性，从而为投资者和监管机构提供更为准确的风险度量和管理工具。特别是EGARCH模型，通过引入非对称项，能够更好地描述信息冲击对股价波动的非对称影响，即“坏消息”对市场的冲击往往大于“好消息”。

2文献综述

在1982年，杰出的计量经济学家罗伯特·恩格尔（Robert-Engle）[1]教授创新性地提出了一种新的模型——“自回归条件异方差模型（ARCH模型）”。该模型专门用于研究经济时间序列。这一杰出贡献使他在2003年荣获了诺贝尔经济学奖。四十多年过去了，ARCH模型及其各种衍生模型，如GARCH、TARCH、EGARCH等，在经济与金融领域的时间序列分析中得到了广泛且深入的应用。国内学者利用这些模型对股票市场的波动性进行了深入研究，刘金全等[3]利用GARCH模型对中国沪深股市的收益率和波动性进行了实证分析，证实了GARCH模型在刻画股票市场波动性方面的有效性。王恒等[4]（2020）则直接利用GARCH模型对沪深股市的收益率波动性进行了研究，并探讨了交易量与波动性之间的关系在预测方面，GARCH模型通过考虑历史波动性信息，能够提供更准确的未来波动性预测。这对于投资者制定投资策略、评估市场风险具有重要意义。李亚静等[5]（2003）基于GARCH模型族对中国股市的波动性进行了预测，发现这些模型能够较好地预测股市的波动性。

随着金融计量学的发展，GARCH模型因其能够较好地捕捉金融时间序列的波动聚集性和厚尾性特征，而被广泛应用于股市波动性的研究中。因此，文章将利用自回归条件异方差模型，即GARCH模型对深证成指日收益率的波动及溢出效应进行实证研究，并做出预测，为投资者进行日收益率的预测并规避风险提供决策依据。

2 研究方法与模型建立

2.1 数据来源与处理

文章选取深证成指的日收益率（对数收益率）进行研究，对大盘收盘指数日收益率的波动进行建模，数据选取时间2014年4月至2024年4月共2434个样本值进行观测。设深证成指第t天的收盘价格为rt（t=1，…2434）对Rt进行自然对数处理：Rt=ln（rt），现研究日收益率。数据处理采用时间序列分析软件Eviews。

2.2 GARCH模型族

ARCH模型的核心思想是，随机扰动项的条件方差受其前期值大小的影响，这实质上意味着残差平方的序列是通过q阶移动平均来拟合当前的异方差函数值。然而，ARCH（q）模型在实际应用中面临一些挑战。为了优化其实用性，Bollerslev[2]在ARCH模型的基础上，进一步提出了广义的GARCH模型。这一模型是ARCH的重要延伸，它不仅有效地降低了滞后阶数，还提高了模型的实用性。其公式表述如下：

其中，是外生变量向量，是系数向量，因此在均值方程是带有误差项的外生变量函数。而是条件方差。在条件方差方程中，可以用来衡量冲击对于金融时间序列数据造成的波动持续性。

Nelson于1991年提出了EGARCH模型，该模型是众多非对称GARCH模型中的一种独特形式。其显著特点在于不对模型内的参数施加非负性限制，从而能够更加精确地探讨信息波动的非对称性。EGARCH模型的条件方差方程可表述为以下形式：

在条件方差方程中，参数测度冲击影响的程度，参数测量信息冲击对条件方差是否对称。

3 深证成指的实证分析

3.1描述性统计

对上证综指日收益率序列进行描述性统计分析，得到描述性分析结果如下。

上证综指日收益率在样本期内平均日收益率为0.00026，显示出在观察期内上证综指的整体收益水平较为稳定，从极值情况来看，最大日收益率为0.05760，最小日收益率为-0.08490，说明在这段时间内，上证综指经历了相对较大的波动，投资者需要警惕市场的不确定性和风险。标准差为0.01296，显示日收益率的离散程度相对较低，但结合偏度系数-0.936998来看，数据分布向左偏斜，即大部分日收益率低于平均值，表明上证综指日收益率更多地聚集在负收益区域。峰度系数为10.18469，远高于正态分布的峰度值，表明数据的分布具有尖峭的特点，存在较多的极端值，说明收益率的分布与正态分布相比呈现出“尖峰厚尾”的分布特征。

3.2平稳性检验

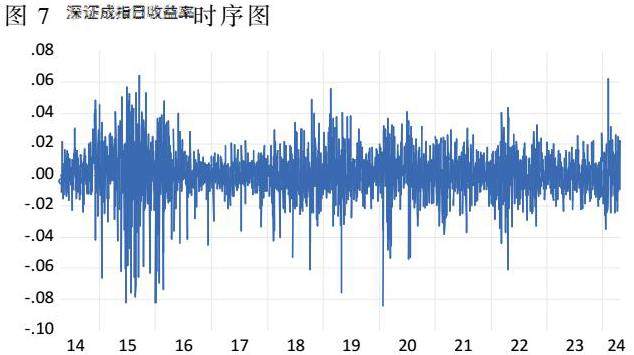
深证成指日收益率的时间趋势图见图2。

该时序图揭示了序列在整体上是平稳的，且主要在零值附近波动。在某些特定月份，序列的波动幅度相对较大，这体现了一种集群效应。为了进一步验证收益率的平稳性，并防止“伪回归”的发生，文章对样本的日收益率序列进行了ADF检验。ADF检验旨在在设定的显著性水平下，检测时间序列是否存在单位根，选择了包含截距项的ADF检验方法。

结果显示（表2），P值为0.0001，小于设定的显著性水平（0.05），则拒绝了随机游走的原假设，即不存在单位根，说明深证成指的日收益率序列是一个平稳的序列。

3.3 ARCH效应检验

为了检验模型是否具备ARCH效应，进行了P-Q检验和ARCH-LM检验。经过对残差数据进行ARCH-LM检验，发现其P值为0，从而拒绝了原假设，这证明了通过最小二乘法得出的残差序列中确实存在ARCH效应。进一步观察残差平方的相关图，当数据滞后10阶时，自相关系数与偏自相关系数的P值都低于0.05。这一结果揭示了模型残差序列具有显著的方差非齐性特征，同时其残差平方之间也呈现出明显的自相关性。因此，文章利用GARCH模型，深入挖掘残差平方序列中所包含的重要信息。

3.4模型估计

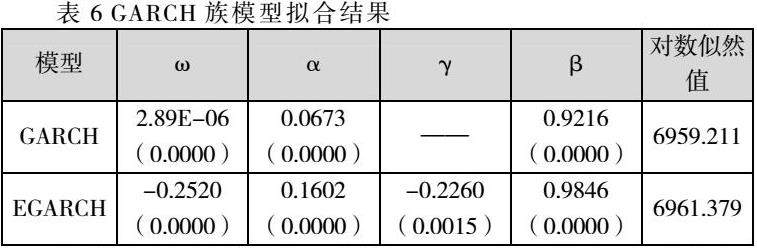
由于GARCH族模型能比较好地描述股票市场“尖峰厚尾”现象，于是主要考虑的模型为GARCH（1，1）和EGARCH（1，1），拟合结果如下表所示：

模型的所有系数所对应的P值均低于0.05的显著性水平，通过了显著性检验。此外，对模型残差进行了Box-Ljung白噪声检验，其结果显示P值超过0.05，因此不能拒绝残差序列不相关的原假设。这表明残差序列是一个白噪声序列，具有平稳性，从而证实了模型具有良好的拟合效果。

在对GARCH（1，1）模型拟合时，深证成指的波动性持续性接近于1，这说明表明随机冲击的影响具有一定程度的持续性，并且股票市场受到的信息冲击在短时间内不能完全消除。在EGARCH（1，1）模型的估计结果中，非对称项系数为-0.0226对应的P值非常小（0.0015），说明该系数在统计上是显著的。这个负的系数意味着信息冲击对于股价波动存在着显著的非对称现象。同时，负的冲击（即“坏消息”）比正的冲击（即“好消息”）对波动性的影响更大，这显示了存在负的溢出效应和杠杆效应，即“坏消息”比“好消息”对波动性的影响更大。

3.4信息冲击曲线

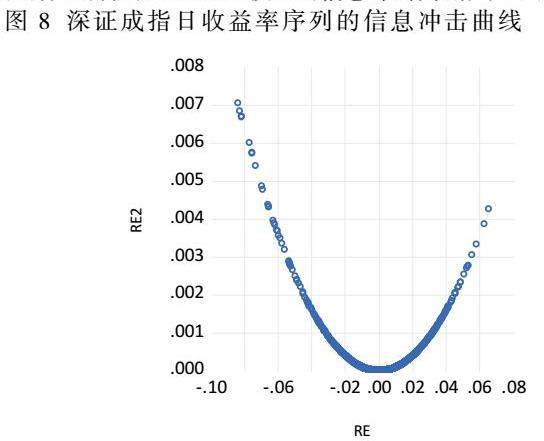
为了进一步说明深证成指存在的波动非对称性，观察正负冲击对波动的影响，绘制出EGARCH模型的信息冲击曲线，如下图所示：

从图中可以看出，左右两侧的信息冲击曲线较为光滑，但左侧信息冲击曲线斜率的绝对值略大于右侧的斜率的绝对值，反映出市场对负面信息的反应更为敏感，波动效应也更为显著，这印证了EGARCH（1，1）模型中的结论。

在相同的信息冲击下，深证成指对于负面消息的波动程度明显高于正面消息。这一特性揭示了市场的风险偏好和市场参与者的情绪变化对指数波动的重要影响。投资者在决策时，应充分考虑这一特性，以便更好地管理风险。

4 结论与建议

文章采用GARCH族模型对深证成指日收益率的波动性进行了深入分析，实证研究了深证成指日收益率的波动性，得出以下结论：

首先，深证成指的日收益率展现出了频繁的波动以及较大的幅度变化。收益率的样本时间趋势并不遵循正态分布，而是显现出“尖峰厚尾”的特征，同时，也存在着显著的波动性聚集现象。其次，经过对深证成指日收益率样本数据的深入分析，发现这些数据表现出平稳性。在构建自回归模型后，可以明显观察到收益率的波动具有异方差性，即存在ARCH效应。这一发现揭示了深证成指的波动性并非保持稳定，而是会随着时间的推移而发生变化。第三，GARCH（1，1）模型的拟合结果显示，深证成指的波动性具有高度的持续性，意味着随机冲击对股市的影响是长期且不易消除的。这一发现对于理解市场风险、制定投资策略具有重要意义。更进一步地，EGARCH（1，1）模型的估计结果揭示了信息冲击对股价波动的非对称现象，即收益率的条件方差对“利空消息”和“利好消息”的冲击具有不对称反映，“坏消息”对波动性的影响显著大于“好消息”，这体现了股市中的杠杆效应。这种非对称性在信息冲击曲线中得到了直观的展现，左侧曲线（代表负冲击）的斜率绝对值大于右侧（代表正冲击），进一步印证了模型的结论。

基于以上发现，文章提出以下建议：

从社会国家的视角出发，政府应深刻认识到股市波动性对社会经济稳定的重要性。由于深证成指的波动性显示出显著的异方差性和高度持续性，政府需强化金融监管力度，确保市场的平稳运行。首先，应完善相关法律法规，为市场提供明确的规则指导，减少不确定性因素。其次，建立高效的市场监控体系，实时监测股市动态，以便及时应对可能出现的市场异常。最后，加大对违规行为的惩处力度，通过严格的执法来维护市场秩序，保护投资者利益。

在资本市场层面，交易所和监管机构应担负起更大的责任。鉴于深证成指的波动性特征，资本市场需要更加精细化的管理策略。一方面，应提升市场透明度，确保所有参与者能够公平获取信息，从而减少信息不对称所带来的市场波动。另一方面，要不断优化交易机制，降低交易成本，提高市场效率。此外，还应加强风险预警和应急响应机制的建设，以便在市场出现异常波动时能够迅速作出反应，维护市场的稳定。

对于企业而言，深证成指日收益率的波动性研究结果提供了重要的管理启示。企业应提高信息披露的透明度，确保财务信息的真实性和准确性。这不仅有助于减少市场对企业经营状况的不确定性，还能增强投资者的信心。同时，企业应加强内部风险管理，建立健全的风险防控体系，以应对可能的市场波动带来的挑战。通过这些措施，企业可以更加稳健地运营，为股东创造长期价值。

对于投资者来说，深证成指的波动性研究结果同样具有重要的指导意义。投资者应提高风险意识，理性看待市场波动。在投资决策时，应充分考虑市场的异方差性和信息冲击的非对称性。这意味着投资者需要更加谨慎地评估投资风险，并根据市场情况灵活调整投资策略。此外，投资者还应关注企业的基本面和长期发展潜力，而非仅仅关注短期的市场波动。

参考文献：

[1]Engle，R.F.Autoregressive conditional heteroskedasticity with estimates of the variance of U.K inflation[J]. Econometrica，1982（50）： 987-1007.

[2]TIM BOLLERSLEV.Generalized autoregressive condition heteroskedasticity[J].Journal of econometrics，1986，31（3）：307-327

[3]刘金全，崔畅.中国沪深股市收益率和波动性的实证分析[J].经济学（季刊），2002（03）：885-898.

[4]王恒.沪深股市收益率波动性及其与交易量的关系研究——基于GARCH模型[J].经济与社会发展研究，2020，（29）：98-99，123

[5]李亚静，朱宏泉，彭育威.基于GARCH模型族的中国股市波动性预测[J].数学的实践与认识，2003（11）.

[6]孟彦菊，尹晓梦.沪市股票日收益率波动性分析——基于GARCH（1，1）模型[J].物流工程与管理，2017，第39卷（5）： 159-160，167

[7]张可可.信息冲击对我国股市的影响[J].时代金融，2021（3）：71-73