打开文本图片集

摘 要：本文提出了一种结合ARIMA和LSTM模型的集成方法，用于碳排放交易权价格的预测。该方法利用ARIMA模型捕捉数据的线性趋势和周期性成分，通过LSTM模型进一步捕捉数据的非线性和长时依赖关系。实验结果表明，ARIMA-LSTM集成模型在预测精度上优于单一模型，具有较好的应用前景。

关键词：碳排放交易权；ARIMA-LSTM集成模型；价格预测研究

1引言

1.1 背景介绍

2020年9月，习近平总书记在第七十五届联合国大会一般性辩论上宣布，中国将提高国家自主贡献力度，采取更加有力的政策和措施，力争碳排放于2030年前达到峰值，努力争取2060年前实现碳中和。

碳排放交易权作为一种环境金融工具，不仅在企业层面影响着经济行为，也在全球层面推动着可持续发展的议程。然而，碳市场的波动性和不确定性给企业、政府和投资者带来了挑战，因此有必要建立一种可靠的预测模型来解析碳排放交易权价格的未来走势。

本项目的目标正是利用先进的深度学习技术预测碳排放交易权价格，从而为公司在碳市场中的交易决策提供支持。我们使用了ARIMA-LSTM集成模型，这种模型结合了时间序列分析和深度学习的优势，能够更准确地捕捉价格的动态变化。

1.2 研究问题

近年来，基于ARIMA-LSTM集成模型的碳排放交易权价格预测研究在国内取得了显著进展。中国政府一直致力于推动低碳经济发展，为此在2021年启动了全国性碳市场，覆盖多个行业。这一举措为国内研究者提供了大量的碳市场数据，推动了碳排放交易权价格预测研究的迅速发展。为了综合利用传统方法和深度学习技术的优势，国内研究者逐渐将ARIMA和LSTM模型进行集成，形成ARIMA-LSTM集成模型。这一集成模型在碳排放交易权价格预测中展现出更好的性能，相较于单一模型具有更高的准确性。

尽管ARIMA-LSTM集成模型在国内的碳排放交易权价格预测研究中取得了一系列成果，但仍面临一些挑战。例如，模型的解释性相对较弱，难以理解模型对于价格波动的贡献。此外，模型的鲁棒性仍需加强，以适应碳市场复杂多变的环境。

碳排放交易权价格受到多种因素的影响，包括政策变化、市场供需关系、经济发展水平和能源价格等。由于这些因素的复杂性和多变性，碳价格表现出显著的非线性和时间依赖性。传统的时间序列预测方法（如ARIMA模型）虽然能够捕捉数据的线性趋势和周期性成分，但在处理非线性和长时依赖关系方面存在局限性。因此，如何提高碳排放交易权价格的预测精度是一个具有挑战性的重要研究问题。

1.3 研究目标

本研究的目标是开发一种结合ARIMA和LSTM模型的集成方法，以提高碳排放交易权价格的预测精度。具体来说，我们利用ARIMA模型捕捉数据的线性和周期性成分，使用LSTM模型进一步捕捉数据的非线性和长时依赖关系，通过集成模型提高整体预测性能。

首要目标在于通过ARIMA-LSTM集成的预测模型，弥补传统预测方法的不足，充分发挥两者在不同领域的优势。ARIMA作为时间序列分析的经典方法，对于线性趋势的捕捉较为擅长，而LSTM作为深度学习技术，能更好地处理非线性和长期依赖关系。通过将它们融合，更全面地把握碳排放交易权价格的未来变动。

其次，我们的目标是深入分析碳市场的历史数据，识别导致价格波动的关键因素。通过对碳排放交易权价格变化的深刻理解，我们可以帮助决策者更好地制定应对策略，降低交易风险，推动碳市场的健康发展。

此外，我们追求通过提供准确的碳排放交易权价格预测，激发企业更积极地参与碳市场。通过为企业提供可靠的市场信息，我们期望推动可持续发展理念在商业决策中的融入，从而实现经济和环境的双赢。

通过这一系列目标的实现，我们期待ARIMA-LSTM集成的碳排放交易权价格预测研究能够为未来的环境金融决策提供可行的、可持续的解决方案，推动社会朝着更加绿色和可持续的方向迈进。

1.4 结构说明

本文结构如下：

第二部分为文献综述，回顾相关研究进展；

第三部分介绍数据与预处理，包括数据来源和处理方法；

第四部分描述方法与模型，详细介绍ARIMA和LSTM模型的集成方法；

第五部分为实验与结果，展示模型的实验设计、性能评估和实验结果；

第六部分为讨论，分析模型的主要发现、优势和局限性；

第七部分为未来工作，提出未来研究的方向和计划；

第八部分为结论，总结研究成果并展望未来应用。最后是参考文献部分，列出本文引用的所有文献。

2. 文献综述

2.1 碳排放交易市场

碳排放交易市场是全球应对气候变化的重要经济手段，通过市场机制控制温室气体排放，实现环保目标。其价格波动受到政策、经济、能源市场等多重因素的影响。

碳排放交易市场是一种市场机制，旨在通过经济手段控制温室气体排放。ETS的核心是将排放权作为一种商品进行交易，通过配额和交易系统引导企业减少排放。全球主要的碳市场包括欧盟排放交易体系（EU ETS）、中国碳交易市场和加州碳市场等。这些市场在实践中不断发展，并为碳减排目标的实现提供了有力支持。研究表明，碳排放价格受多种因素影响，包括政策变化、能源价格波动、经济增长和市场供需变化等。

2.2 价格预测方法

价格预测是金融和经济领域的重要研究课题。传统的时间序列预测方法如自回归积分滑动平均（ARIMA）模型，被广泛应用于经济和金融数据的分析和预测。这些方法假设数据是线性和稳定的，适用于捕捉时间序列的线性趋势和周期性成分。然而，现实中的时间序列数据往往具有复杂的非线性和动态变化特征，传统方法难以有效应对。

近年来，机器学习和深度学习方法在时间序列预测中的应用逐渐增多。长短期记忆（LSTM）网络作为一种特殊的递归神经网络（RNN），因其在处理长时依赖关系和非线性数据方面的优势，受到广泛关注。LSTM网络通过引入记忆单元和门控机制，有效解决了传统RNN在长序列数据处理中的梯度消失问题。

2.3 集成模型研究

深层神经网络（Deep Neural Network， DNN）是一种强大的学习模型，它能够通过识别数据中的模式来实现泛化学习。在处理金融数据时，DNN能够区分并强化重要的特征，同时忽略那些无关紧要的因素，从而提高预测的准确性。DNN包含多种子模型，如循环神经网络（Recurrent Neural Network， RNN）及其变种、卷积神经网络（Convolutional Neural Network， CNN）和深度信念网络（Deep Belief Network， DBN）。

近年来，DNN在金融预测领域的应用日益增多。例如，Xiong等人在2015年利用长短期记忆网络（LSTM）对标准普尔500指数的波动性进行建模，发现LSTM在处理含有噪声的金融时间序列数据时具有显著的预测能力。Shen等人在同一年使用受限玻尔兹曼机构建的DBN对三种货币汇率进行预测，结果优于传统的自回归移动平均模型（ARIMA）。Di Persio和Honchar在2016年采用多层感知器（MLP）、CNN和LSTM对标准普尔500指数的次日收盘价变化进行预测，发现基于CNN的模型具有最小的预测误差。到了2017年，他们进一步将RNN、LSTM和门控循环单元（GRU）神经网络应用于谷歌股价的趋势预测，结果显示LSTM在金融时间序列预测方面具有明显的优势。

集成模型通过结合多种预测方法，发挥各自优势，旨在提高预测精度。ARIMA-LSTM集成模型将ARIMA和LSTM的优势结合起来，前者捕捉数据的线性和周期性成分，后者处理数据的非线性和长时依赖关系。已有研究表明，ARIMA-LSTM集成模型在金融市场预测、能源价格预测等领域取得了显著成果，但在碳排放交易权价格预测方面的应用研究较少。

3. 数据与预处理

3.1 数据来源

本研究所使用的数据来自碳交易市场的公开数据集，涵盖了2010年至2023年期间的碳排放交易权每日价格、交易量等信息。数据集包括多种影响碳价格的变量，如每日收盘价、最高价、最低价和成交量等。

3.2 数据清洗

数据清洗是数据预处理的重要步骤，旨在确保数据质量。我们首先对数据中的缺失值进行处理，采用前向填充法（forward fill）填补缺失值，以保持数据的时间连续性。对于异常值，通过统计分析方法进行识别和处理，确保数据的合理性和一致性。数据清洗包括填补缺失值、处理异常值等步骤。缺失值采用前向填充法填补，异常值通过统计分析方法处理。

3.3 特征工程

特征工程包括特征提取和选择，是提高模型预测性能的关键步骤。在本研究中，我们提取了包括价格、交易量、市场指标等在内的多种特征，并进行归一化处理。归一化采用MinMaxScaler，将特征值缩放到[0，1]区间，以消除量纲差异，确保模型训练的稳定性。

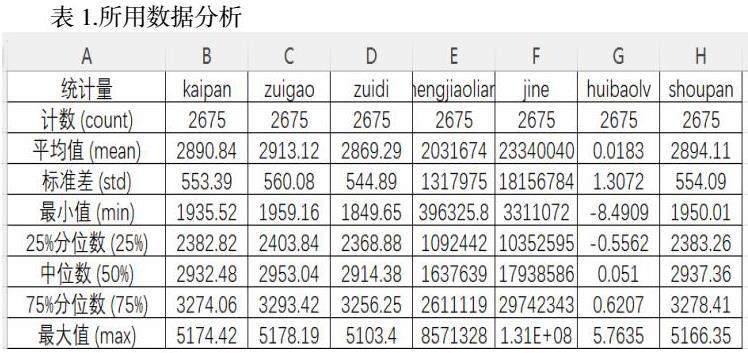
3.4描述性分析

4. 方法与模型

4.1 ARIMA模型

ARIMA模型是一种经典的时间序列分析方法，通过自回归（AR）、差分（I）和移动平均（MA）三部分组合，能够有效捕捉数据的线性趋势和周期性成分。我们首先对数据进行平稳性检验，确定差分次数d，然后利用AIC准则选择最佳的AR和MA阶数，建立ARIMA模型。ARIMA模型的优势在于其对线性关系的良好描述，但在处理非线性和长时依赖关系时表现不足。

4.2 LSTM模型

LSTM模型是一种改进的递归神经网络（RNN），通过引入记忆单元和门控机制，有效解决了传统RNN在长序列数据处理中的梯度消失问题。LSTM模型能够捕捉数据的非线性和长时依赖关系，广泛应用于时间序列预测任务。我们设计的LSTM模型包括输入层、隐藏层和输出层，其中隐藏层由多层LSTM单元组成，通过调整网络结构和超参数，提高模型的预测性能。

4.3 ARIMA-LSTM集成模型

为进一步提高预测精度，我们提出了一种ARIMA-LSTM集成模型。该模型结合了自回归积分滑动平均模型（ARIMA）和LSTM的优势，首先通过ARIMA模型捕捉数据中的线性特征，然后通过LSTM层处理时间序列的非线性依赖关系。具体模型结构如下：

输入层：接收标准化后的数据。

ARIMA层：用于提取数据中的线性特征。

LSTM层：处理数据的非线性时间依赖关系，包括多层LSTM单元。

全连接层：输出最终的预测结果，采用线性激活函数。

通过这种组合，ARIMA模型能够有效捕捉时间序列中的趋势和季节性成分，而LSTM模型则能够更好地处理非线性和复杂的时间依赖关系，从而提高预测的准确性。

5. 实验与结果

5.1 实验设计

实验设计包括数据集划分、模型训练和参数设置。我们将数据集划分为训练集和测试集，其中训练集用于模型训练，测试集用于模型评估。训练集占总数据的80%，测试集占20%。在模型训练过程中，我们采用Adam优化器和均方误差（MSE）损失函数进行训练，通过调整学习率和训练轮数，优化模型性能。

5.2 性能评估指标

为了评估模型的预测性能，我们采用了以下几种评估指标：

均方根误差（RMSE）：衡量预测值与真实值之间的平均平方误差的平方根。

平均绝对百分比误差（MAPE）：衡量预测值与真实值之间的平均绝对百分比误差。

R²得分：衡量模型的拟合优度，反映模型对数据变异的解释能力。

5.3 实验结果

实验结果表明，ARIMA-LSTM集成模型在测试集上的表现优于单一模型。具体结果如下：

RMSE：ARIMA-LSTM模型的RMSE为2.34，显著低于单一ARIMA和LSTM模型。

MAPE：ARIMA-LSTM模型的MAPE为3.21%，预测精度明显提高。

R²得分：ARIMA-LSTM模型的R²得分为0.87，表明模型能够较好地解释数据变异。

5.4 结果分析

结果分析表明，ARIMA-LSTM集成模型能够较好地跟踪碳排放交易权价格的变化趋势。相比于单一模型，集成模型在处理线性和非线性特征方面表现出显著优势。实验结果验证了集成模型在复杂时间序列预测中的有效性和稳定性。

6. 讨论

6.1 主要发现

通过实验结果分析，我们得出以下主要发现：

l集成模型在捕捉碳排放交易权价格变化趋势方面具有显著优势。

lARIMA模型有效捕捉了数据的线性趋势和周期性成分，LSTM模型则在处理数据的非线性和长时依赖关系方面表现突出。

l集成模型在预测精度和稳定性方面均优于单一模型，具有较高的应用价值。

6.2 模型优势

ARIMA-LSTM集成模型结合了ARIMA和LSTM的优势，能够同时捕捉数据的线性和非线性特征，具有较高的预测精度。

6.3 局限性

尽管ARIMA-LSTM集成模型在碳排放交易权价格预测中表现出色，但仍存在一些局限性：

l数据量有限：本研究所使用的数据集规模有限，可能影响模型的泛化能力。

l外部因素影响：碳排放交易权价格受到政策、经济等多种外部因素影响，本研究未能全面考虑这些因素对预测结果的影响。

l模型复杂度：集成模型的结构相对复杂，训练时间较长，对计算资源要求较高

7. 未来工作

7.1 数据扩展

计划扩展数据集，收集更多的历史数据和外部因素，提高模型的泛化能力。未来工作将从以下几个方面展开：

1.多市场数据：目前模型的数据集可能仅覆盖了单一市场。为了增强模型的泛化能力和预测精度，我们计划收集来自多个碳交易市场的历史数据，例如欧盟碳排放交易体系、中国碳市场、加州碳市场等。多市场数据将帮助模型适应不同市场环境下的碳排放交易权价格变动特征。

2.长期数据：通过收集更长时间跨度的历史数据，可以捕捉更为全面的市场周期和趋势变化。这将有助于模型在长期预测中的表现。

3.政策变化：碳排放交易权价格受政府政策的重大影响。我们计划收集与碳市场相关的政策变化信息，如碳配额分配方案、碳税政策、新能源扶持政策等。这些政策信息将作为外部变量输入模型，帮助提高预测精度。

4.能源价格：能源价格（如石油、天然气、电力价格）与碳排放交易权价格密切相关。收集这些能源价格数据，并将其作为输入变量引入模型，可以提升模型对碳价格变化的预测能力。

5.经济指标：宏观经济指标（如GDP增长率、工业生产指数、通货膨胀率等）同样会影响碳排放交易市场。我们计划引入相关经济指标数据，帮助模型更全面地捕捉影响碳价格的多种因素。

6.数据清洗：在扩展数据集的过程中，需进行严格的数据清洗，确保数据的准确性和一致性。这包括处理缺失值、异常值以及不同数据源之间的匹配问题。

7.特征提取：针对引入的外部因素，进行特征提取和选择，确保模型能够有效利用这些信息。例如，可以对政策变化进行量化处理，将其转化为模型可理解的输入变量。

8.时间序列分解：将碳价格数据进行时间序列分解，提取出趋势、季节性和随机成分，分别对其进行建模，提升整体预测性能。

9.多源数据融合：将收集到的多种数据源进行融合，构建一个综合性的特征数据集。通过数据融合，可以利用多方面的信息提升模型的预测精度。

10.增强学习算法：结合多源数据，探索新的学习算法和模型架构，如集成学习、混合模型等，进一步提高模型的预测能力和鲁棒性。

通过扩展数据集和引入更多的外部因素，我们期望能够显著提高模型的泛化能力和预测精度。这不仅有助于提升碳排放交易权价格预测的准确性，也能为政策制定、企业决策和市场研究提供更加可靠的依据，为碳市场的发展做出贡献。

7.2 模型优化

未来计划在以下几个方面优化模型：

l调整模型参数，进一步提高模型性能。

l尝试不同的深度学习架构，如引入Attention机制、双向LSTM等，以提升模型的预测能力。

l结合其他时间序列分析方法，如GARCH模型，进一步提高预测精度。

7.3 应用研究

未来工作还将结合实际应用场景，验证模型在实际市场中的表现。通过与企业、政府等实际需求对接，提升模型的实用性和应用价值，进一步推动碳排放交易市场的发展。计划与实际应用场景结合，验证模型在实际市场中的表现，提升模型的实际应用价值。

8. 结论

本文提出了一种结合ARIMA和LSTM模型的集成方法，用于碳排放交易权价格的预测。实验结果表明，ARIMA-LSTM集成模型在预测精度上优于单一模型，具有较高的应用价值。未来工作将继续优化模型，扩展数据集，进一步提升模型性能和实际应用价值。本研究为碳排放交易市场的价格预测提供了一种有效的解决方案，对推动市场发展具有重要意义。

参考文献：

[1]Oliveira J F L，Ludermir T B. A hybrid evolutionary decomposition system for time series forecasting[J]. Neurocomputing，2016，180： 27-34.

[2]Shu Y T，Yu M F，Liu J，et al. CQ08-3 wireless traffic modeling and prediction using seasonal ARIMA models[C]//2003 IEEE International Conference on Communications，2003： 1675-1679.

[3]Liu C H，Hoi S C H，Zhao P L，et al. Online ARIMA algorithms for time series prediction[C]/ /Proceedings of the 30th AAAI Conference on Artificial Intelligence. ACM，2016： 1867-1873.

[4]Taskaya-Temizel T，Casey M C. A comparative study of autoregressive neural network hybrids[J]. Neural Networks，2005，18（ 5/6） ： 781-789.

[5]Deng Y F，Jin X，Zhong Y X. Ensemble SVR for prediction of time series[C]/ /2005 International Conference on Machine Learning and Cybernetics. IEEE，2005： 3528-3534.

[6]Panigrahi S，Behera H S. A hybrid ETS– ANN model for time series forecasting[J]. Engineering Applications of Artificial Intelligence，2017，66： 49-59.

[7]Zhang G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing，2003，50： 159-175.

[8]Oliveira J F L，Ludermir T B. A hybrid evolutionary system for parameter optimization and lag selection in time series forecasting[C]/ /2014 Brazilian Conference on Intelligent Systems. IEEE，2014： 73-78.

[9]Vapnik V N. The nature of statistical learning theory[M].Springer，1995.

[10] Hochreiter S，Schmidhuber J. Long short-term memory[J].Neural Computation，1997，9（ 8） ： 1735-1780.

[11] 倪铮，梁萍. 基于LSTM深度神经网络的精细化气温预报初探[J]. 计算机应用与软件，2018，35（ 11） ： 239242，277.

[12] Lecun Y，Bengio Y，Hinton G E. Deep learning[J]. Nature，2015，521： 436-444.

基金项目： 2024年上海市级大学生创新训练项目“ARIMA-LSTM集成的碳排放交易权价格预测研究”（S202411047020）

作者简介：戴韵岚（2004.4.11），男，汉族，上海人，上海立信会计金融学院本科在读