打开文本图片集

摘要：系统思维是指把认识对象作为系统，从系统、要素、环境的相互作用中区综合考察认识对象的思维方法.提升系统思维水平就是培养学生发现、提出、分析和解决问题能力的关键措施，同时培养学生的整体观和全局观.以“直线与圆的位置关系”教学设计为例，借助关键问题，注重研究对象之间的相互转化，阐述系统思维的重要性.

关键词：系统思维;关键问题;直线与圆位置关系

一、教学内容及其解析

本节课选自冀教版《义务教育教科书 数学》九年级下册第二十九章第二节，主要内容为直线与圆的位置关系的相关概念及其性质和判定方法.

本节课是在学生学习了点与圆等的位置关系的基础上进行的. 而直线与圆三种位置关系的概念也是类比点与圆的三种位置关系，围绕直线与圆的公共点这一几何元素给出，同时借助教具进行动态操作，让学生能够更加直观地感受三种位置关系，丰富其概念的获得过程.

此外，本节课研究思路也符合几何图形的一般研究思路：定义--性质--判定. 同时，本节课的学习思路和方法同样可以类比到后续章节的学习中去.

二、教学目标及其解析

教学目标：

1.经历直线与圆相交、相切、相离三种位置关系概念的获得过程;

2.理解直线与圆有相交、相切、相离三种位置关系;

3.探索直线与圆三种位置关系的性质和判定，经历位置关系和相应数量关系的相互转化;

三、学生学情分析

学情分析：

1.知识层面：学生已系统研究了圆的概念及性质，对点与圆的位置关系也有相应了解;

2.探索层面：学生具有一定的研究“直线型”几何图形性质、两个几何图形关系的经验，但对于圆和其他几何图形的关系的学习，积累的经验较少，需要从几何研究本质出发，从“数”和“形”两个角度揭示直线与圆的位置关系，将新问题转化为旧知识进行解决;

教学重点：理解“直线与圆的三种位置关系”与“圆心到直线的距离d与半径r的数量关系”的对应与等价关系.

教学难点：探索如何用数量关系刻画直线与圆的三种位置关系.

四、教学策略分析

本节课主要采用问题式探索法引导学生归纳概括直线与圆相交、相切、相离三种位置关系的概念，探索直线与圆位置关系的性质和判定.

五、教学过程

1. 复习回顾，规划思路

【问题1】除了点与圆的位置关系，我们还可以研究哪些几何图形与圆的位置关系？

还可以研究直线与圆、角与圆、三角形与圆、多边形与圆的位置关系.

【追问】你认为先研究哪个位置关系好？为什么？

2. 直观感知，归纳概念

【问题3】在纸上画一条直线，借助教具圆环，你能发现直线与圆有哪些位置关系？

【问题4】你分类的依据是什么？

当直线与圆有两个公共点时，直线与圆相交，公共点叫做交点，直线叫做割线;

当直线与圆有一个公共点时，直线与圆相切，公共点叫做切点，直线叫做切线;

当直线与圆没有公共点时，直线与圆相离.

3.研究性质，转化问题

研究几何图形的性质本质就是研究相关几何要素之间确定的位置关系和数量关系.

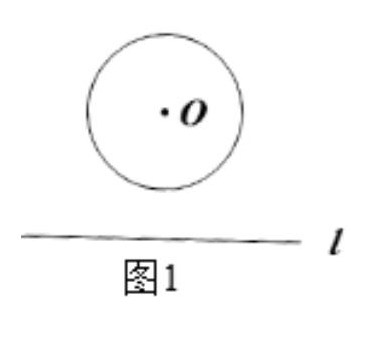
【活动一】如图1，已知直线 l 平行于水平面，⊙O的位置和大小不变，向上平移直线l，思考如下问题，和同学交流看法.

【问题4】直线 l 向上平移过程中，直线 l 与⊙O经历了怎样的位置关系？

【问题5】直线上哪个点最先成为公共点？怎样确定这个点的位置？

【设计意图】借助问题5，引导学生根据“垂线段最短”领悟到：直线与圆位置关系的变化会使直线上某个（些）点成为直线和圆的公共点;

值得注意的是：以上探究过程对直线的位置和运动方式进行了特殊化规定，如果是任意位置的直线，以任意方式靠近圆，刚刚的方法是否依然适用？答案是肯定的！

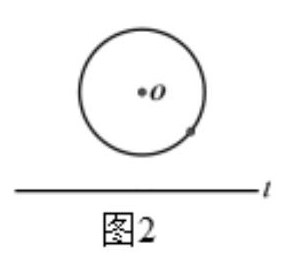
【活动二】如图2，直线 l 位置不变，⊙O圆心位置不变，改变半径大小，思考如下问题，并和组内同学交流看法.

【问题6】直线上哪个点最先成为公共点？

【问题7】当直线 l 与⊙O相交、相切、相离时，这个点和⊙O有怎样的位置关系？为什么？

【问题8】你能得到哪些直线与圆在三种位置关系下的哪些性质呢？

当直线l与圆相交时，圆心到直线l的距离d

当直线l与圆相切时，圆心到直线l的距离d = r;

当直线l与圆相离时，圆心到直线l的距离d>r.

4.研究判定，探究本质

【问题9】可以从哪几个方面研究直线与圆位置关系的判定方法？

【设计意图】借助两个问题，引导学生从定义、性质等角度探究直线与圆相交、相切、相离的判定方法. 此时，学生可能会对特殊情况：相切的判定方法提出一些看法，教师应该予以相应的引导，并留到下节课进行探究.

5.总结提升

【问题10】本节课我们研究了哪些内容？是按照怎样的顺序展开的？

【问题11】在探索性质和判定的过程中，用到了哪些思想方法？

【问题12】接下来，你还想研究哪些问题？你是怎么想到要研究这些问题的？

【设计意图】引导学生回顾本节课所学知识，理解直线与圆有三种位置关系;通过对性质和判定方法的探索，掌握“几何要素中特殊位置关系与特殊数量关系存在联系”、“将未知转化为已知”，进一步认识数学思想、数学方法、积累数学活动的经验. 同时，借助本节课的学习过程，发现和提出新的问题，借助已有的学习经验和思想方法进一步分析和解决问题.

参考文献：

[1]章建跃. 数学教育随想录[M]杭州：浙江教育出版社，2017.

[2]伍春兰. 直线与圆位置关系的数学味道[J]数学通报，2016（55）：34-36.