打开文本图片集

摘要：“重构式”被认为是数学史融入数学教学最高层次的方式。以“椭圆的定义与方程”为例，具体阐释一下几个问题：第一，什么是数学史“重构式”？第二，为什么要进行数学史重构？第三，如何进行椭圆数学史重构？最后提出信息技术支持下数学史重构实践路径：重构数学史料，引导学生“再创造”和“再发现”;培育HPM教研共同体;重视信息技术在数学教学中的渗透。

关键词：数学史“重构式”;高中数学教学;信息技术;椭圆

引言

立足于课本研究椭圆的定义与方程，结合高考评价体系的“一核、四层、四翼”的积极育人导向下高考试题特征分析中发现，新高考中显性或隐性地考察与数学文化相关的数学知识和方法原理[1]。而数学史的全教育价值有：知识的和谐、思想或方法的之美、探究的乐趣、能力的提高、文化的魅力和道德教育的可用性[2]。教师需要将静态数学史创造性地融入动态教学课堂，实现以核心素养为指挥棒、数学史料和信息技术为辅助的教学重构实践策略。数学史融入课堂教学指向数学内容客体本身，而融入数学史的终极目标是要落实到学生发展之上，而驱动性问题链设计在数学史融入数学教学实践中搭建起“史学形态”向“教育形态”转化的桥梁[3]。

1.什么是数学史“重构式”？

汪晓勤教授等人在西方学者研究的基础上结合我国的数学教学实践特色，整合和改进出数学史融入数学教学的四种本土化方式。“重构式”被认为是数学史的最高层次融入方式，类似于Tzanakis&Arcavi的间接运用法和Jankvist的基于历史法，数学史“重构式”是借鉴或重构知识的发生、发展历史，这意味不是还原数学史，而是要教活数学史[4]。

2.为什么要进行数学史重构？

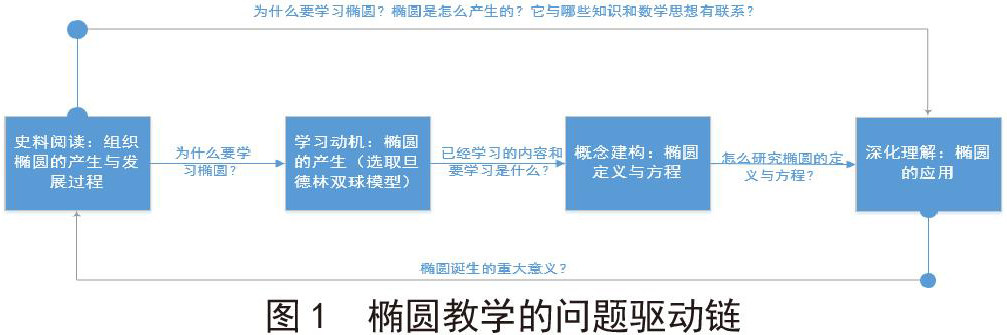
教科书中直接从上一节的直线与圆直接过渡到圆锥曲线，这样的处理符合学生的认知发展，但没有指明为什么要学习圆锥曲线，缺乏具体的学习情境，很难驱动学生积极思考问题，无法体会解析几何的历史渊源，更无从知晓数学家经历的困惑，因此，可以基于HPM教学法，将数学史进行“重构”，提炼出驱动问题链（如图1所示），使其内容更加适合于课堂教学，让学生经历相似的学习困难，同时也丰富教材内容。

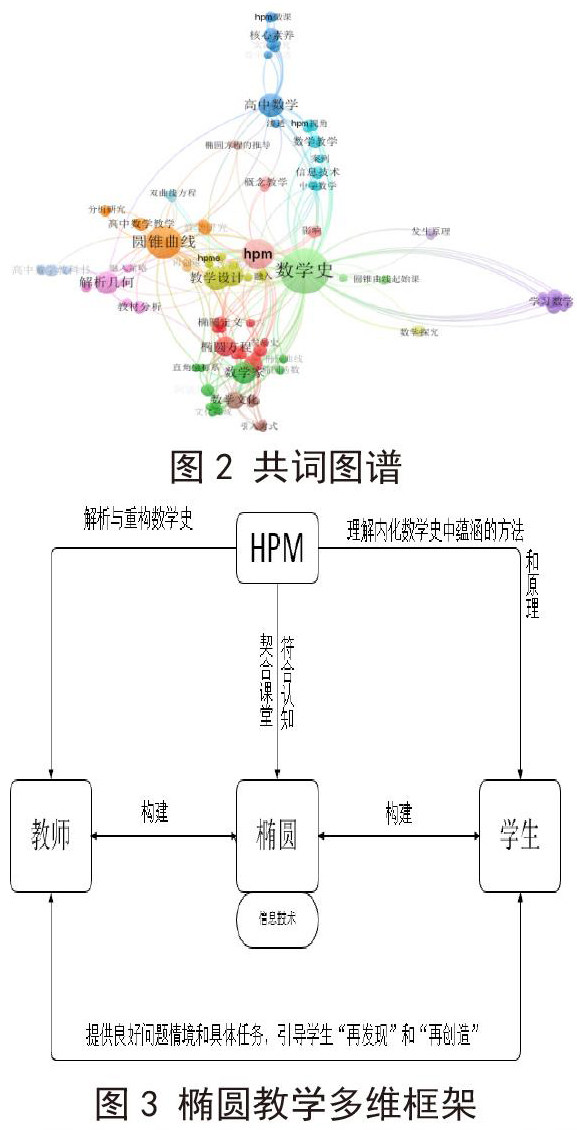
HPM的椭圆教学受到越来越多的学者关注，其研究也得到持续深入的发展，随着新一轮课程改革推进，整体呈上升趋势。选择CNKI期刊有效文献54篇为样本，其中有53.7%来源于期刊，40.74%来源于硕士论文，5.56%来源于博士论文。在研究中采用VosViewer软件对椭圆及数学史进行全景式图谱分析，见图2，基于图谱从不同角度对HPM视角下的椭圆教学进行研究，从而综合得出一个较为完善的椭圆教学切入整体框架，见图3。

学生在高中阶段，已经具备空间想象能力和逻辑推理能力，可根据教师提前布置的研究性学案进行预习，搜索回顾已有知识经验，比如已经学习过借助坐标法研究直线与圆的方程，初步体验了数形结合的思想。在教师启发之下能概括椭圆定义并能用精准数学语言进行描述，与教师不断互动中同化平衡椭圆知识。

3.如何进行椭圆数学史重构？

3.1重循发展之路，感知曲线之美

梳理圆锥曲线的知识脉络要兼顾数学知识与历史时间序列，从高观点下去审视圆锥曲线，厘清圆锥曲线的由来及数学家所经历过的困惑和所采用的思想方法，感受数学知识背后火热的思考。将提前做好HPM微课或者提供素材让学生创作加工成关于圆锥曲线的话剧作为课堂“导入”环节，可以丰富在教学实践中的课堂内容，增加课堂内容的趣味性和实用性，使得课堂内容“单一性”向“多元性”转化，能充分调动学生多感官的求知欲。

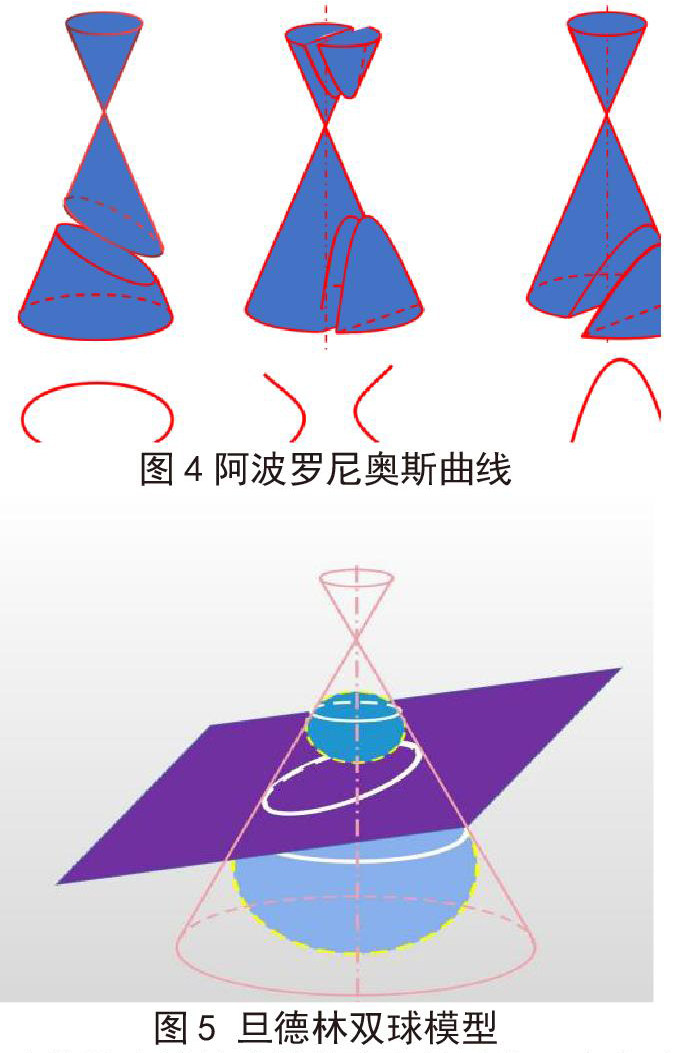
比如阿波罗尼奥斯用平面从不同角度去截同一圆锥得到三种曲线（见图4），基于欧几里得、阿里斯泰乌斯和阿基米德等前人的研究基础上仿《欧几里得》整理了《圆锥曲线论》一书。旦德林构造旦德林双球模型（见图5），巧妙揭示了椭圆在数量关系和几何关系上的本质联系，借助信息技术的展示，无需太多的学科知识背景，学生就能理解椭圆的本质和奥秘，这个证明本身具有创造性的关键一步在于：引入两个球，而其他证明步骤就比较循规蹈矩，而这样的神来之笔，是数学教育发展令人深醒的一面，可能会问这样的灵感是从何而来？就像砸中牛顿的苹果变成万有引力定律一样神奇。

需要明确数学史是辅助教学育人的功能，本文选择旦德林双球模型重构，原因如下：第一，旦德林双球模型与新授课内容高度契合，在椭圆数量及几何关系本质上保持高度一致，统一了椭圆在第一定义与截面定义。第二，旦德林双球的选取充分考虑了学生的学情，符合学生认知基础，但是旦德林双球中所添的辅助线是一个难点，对学生而言是一个新鲜领域，可以激发学生的探求欲望。第三，旦德林双球构造巧妙，可以阐释数学之美，同时将一个静态的知识点形成动态的知识发展链，成为学生学习源源不断的源泉。

3.2.1重建椭圆之史，形成认知规律

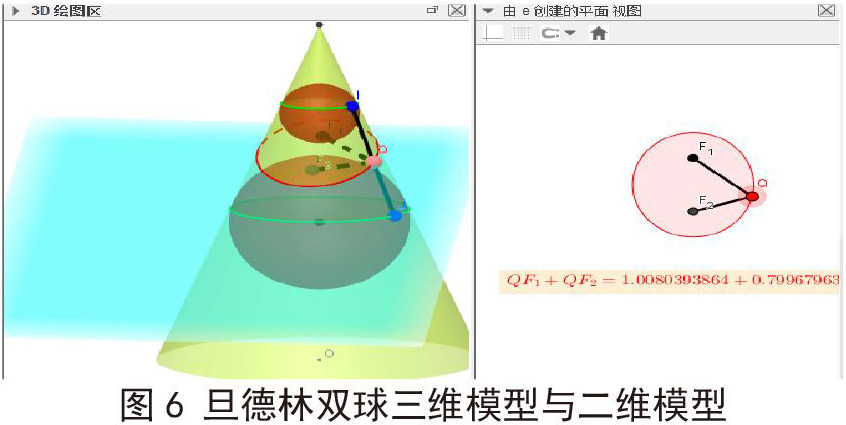
教师通过GeoGebra动态展示旦德林双球可视化模型（图6）。GGB将旦德林双球模型的三维空间上的相切关系转化为二维平面内的相切关系很直观地呈现给学生，在动画模式之下追踪动点Q的轨迹，并动态显示的的数值。其中两个球体与圆锥相切，并且在曲线内部引入了两个特殊点，即两球体和截面的切点，将这些焦点与椭圆上某点连接起来，这两条线特殊之处在于它们并不是单纯地与两球相交而已，而是它们与两球的交点就是切点，那么这两条线的长度之和是多少？通过建立几何关系转换，对在有球体和圆的情况，线段“等长转换”的方法直中圆和球定义的要害，显而易见这是一个典型案例。

3.2.2动手“两钉一绳子”实验，完善椭圆定义

学生在动手实验活动过程中将“学知”与“学做”统一起来，学生在追踪笔尖动点轨迹形成的过程中，体验“做”数学的快乐。教师借助GGB，将数据不断调整，直观感受到不同的数据对图形形状的影响，体现了信息技术化静为动、化抽象为形象调动学生多感官的优越性，帮助学生发现数学史内容和数学课程内容实质性联系，从而加深对于数学知识的理解，提高了课堂的实效性。

3.3重历思想方法，发展数学思维

由椭圆动点轨迹的对称性和数量关系，可程序转化为：位置关系→ 数量关系→关系，坐标法的本质就是通过形数之间关系的转化研究椭圆的性质与方程。这种数形结合思想贯穿圆锥曲线学习的始终，在求解椭圆轨迹方程中需要培养和训练学生的思维模式“建设限代化”。

建：通过给学生看不同坐标系下的椭圆。让学生亲历不同坐标系下椭圆的建立，这样学生更能明白椭圆方程的“标准”所在。

这是建立在笛卡尔和费马发明的坐标法之上，整个计算过程很自然，是现在教科书采用的方法之一，但是其计算量很大。那么还有没有别的推导方法呢？根据构造出，那么令，就有，接下来怎么化简呢？

和差术是洛必达的推导方法，技巧性很强，但是，的设法具有对称性，是椭圆的对称性在代数上的一种体现。

平方差法是赖特通过构造出的对偶式，再通过消元法解出。

4.研究结论及启示

4.1解析与重构数学史料，引导学生“再创造”和“再发现”

通过对具体案例重构“椭圆历史”：重循发展之路，感知曲线之美→重建椭圆之史，形成认知规律→重历思想方法，发展数学思维。在这个重构过程中，教师提供良好问题情境和明确任务，学生“再发现”和“再创造”课堂知识，这里需要指出的是：“再发现”和“再创造”是主观意义上的发现和创造，对于教师来说课堂内容都是已知的结论，而从学生角度来看却是发现和创造，那么也就是学生在教师的指导帮助之下可以生成构建自己的知识体系。

4.2培育基于HPM的教学研共同体

建立起学生、一线教师和科研团队之间三位一体的多重反馈共同体制度，教师在先进的教育理念指导下，挖掘适宜的数学史料进行科学的教学实践，不断实际教学中检测、总结和反思其教学效果，并提供改进方案，建设更有效的数学文化课堂，实现数学史的“问题化”“教育化”。构建HPM教研共同体的主要策略与路径主要有以下两点：

（1）建立基于互联网+的多元化HPM课程教学环境。改变传统单一维度的自我教学模式向多维度群体教学模式转化，创造多元化的互助教学空间，提升数学史融入实际课堂的有效性。发挥高校与中小学一线教师共同教育优势。

（2）加强HPM教师队伍建设，优化教研共同体教育体系。

4.3重视信息技术在HPM课堂教学的渗透

HPM要适应时代发展，需要不断摸索数学史融入课堂教学的新模式、新方法。比如将新兴的信息化VR情境教学融入课堂实践中，让学生身临其境感受数学史的“温度”。

参考文献：

[1]王婷，李祎.基于数学文化的高考试题分析特征分析[J]，数学通报，2021，60（6）：51-54

[2]Wang X Q ， Qi C Y ， Wang K . A Categorization Model for Educational Values of the History of Mathematics[J]. Science & Education， 2017， 26（2）：1029-1052.

[3]孟梦，李铁安.“问题化”：数学“史学形态”转化为“教育形态”的实践路径[J].数学教育学报，2018，27（3）：72-75

[4]汪晓勤，HPM的若干研究与展望[J].中学数学月刊，2012（2）：1-3

[5]徐章韬，汪晓勤，梅全雄.认知的发生原理及其教学工程化[J].数学教育学报，2012（1）：26-30

[6]汪晓勤，椭圆方程旅[J].数学通报，2013，53（4）：52-54

[7]Wang K ， Wang X Q ， Li Y ， et al. A framework for integrating the history of mathematics into teaching in Shanghai[J]. Educational Studies in Mathematics， 2018.