
- 收藏
- 加入书签
基于翻转课堂下的
——有理数的乘法教学
中图分类号:G4 文献标识码:A
《有理数的乘法》是人教版数学七年级上册第一章第四节第一课时的内容。我在教这一课时,始终觉得课堂过于单调,学生能比较快的观察得出有理数的乘法法则,然后大部分费时间就用来进行法则的巩固,总感觉对于学生的思维方式的发展,以及对数学学习兴趣的激发不是很到位,所以我对本节课进行了反转课堂教学模式下的新设计。
一、检查课前预习情况
之前,我已经把今天要学习的内容,以及学习视频发给了学生,并留了几道思考问题,所以今天上课前10分钟对学生的自学效果进行一个简单的反馈。
预习作业:
要求1:看完视屏后完成上面算式的填空。
问题1:从上往下看,第一列算式中,你从中发现的规律是:前一乘数( ),后一乘数逐次( ),积逐次( )。
问题2:从上往下看,第二列算式中,你从中发现的规律是:前一乘数逐次( ),后一乘数( ),积逐次( )。
问题3:从上往下看,第三列算式中,你从中发现的规律是:前一乘数( ),后一乘数逐次( ),积逐次( )。
要求2:把上面的所有算式按“同号两数相乘”“异号两数相乘”“与0相乘”这三种情况进行分类,并完成下列填空:
两数相乘,同号( ),异号( ),并把( )相乘.任何数同0相乘,都得( ).
问题:请同学们仿照上面的算式,自己也写几组算式来说明“要求2”的合理性。
以上是我们本节课的课前任务单,上课前十分钟是对任务单的一个检查,目的是看看学生的自学情况,对于本节课的内容具体掌握到了哪一步,还有就是通过生生、师生之间的交流,再次巩固本节课的基础知识。
二、古往今来、乘法有理
根据课前检测,我发现学生对本节课所要掌握的重难点已经突破到位了,接下来我们要了解的就是有理数乘法的历史背景和学生感兴趣的不同乘法解释模型。
1、有理数乘法的历史简介:
师:有同学知道有理数乘法的历史吗?
负数的概念与运算法则有着漫长的历史发展过程。负数概念以及负数的加减运算法则最早诞生于中国。刘徽在《九章算术》注中称:“今两算得失相反,要令正负以名之。”
公元7世纪,印度数学家婆罗摩笈多(598- -670)也明确提出了正负数的概念以及四则运算法则:“正负相乘得负,两负数相乘得正,两正数相乘得正。”
在中国,13世纪数学家朱世杰在《算学启蒙》中首次提出负数的乘除运算法则:“明乘除法,同名相乘得正,异名相乘得负。”
在《计算之书》中,斐波那契已给出并“证明”了“负负得正”的法则。
16世纪,德国数学家斯蒂菲尔(1487- 1557)在《整数算术》(图4- 1)中给出乘法的符号法则:“同号相乘为正,异号相乘为负。”
17世纪初,德国数学家克拉维斯(1538- -1612)在《代数学》中给出如下符号法则:“正数乘以正数,或负数乘以负数、乘积为正数;正数乘以负数,或负数乘以正数,乘积为负数。”......
师:所以,我们发现有理数的乘法有着悠久的历史,同学们下去可以在找找与它有关的知识和故事。
2、有理数乘法的模型
师:对于有理数乘法的解释,国内外很多数学家对其创造了解释模型,同学们想了解哪种,我们可以一起来看一下。
课件上出示各种展示模型的名称,请学生选择,老师进行展示。
1、运动模型、2、水面升降模型、3、债务模型
4、好人模型、5、减法模型 ......
学生比较感兴趣的是好人模型和运动模型,接下来,我们对这两个模型一一进行了交流学习。
师:由于时间的关系,我们只了解了两个简单的模型,对于有理数的乘法的解释模型除了老师展示出来的这五种,还有很多别的模型,有兴趣的同学可以下去查阅相关资料,同学们也可以根据我们的生活经验自己创造一个能解释有理数乘法的模型,欢迎大家来找我继续交流。
反思:经过这一次的课堂教学方式的调整,我感觉学生对于有理数的乘法研究有了很高的兴趣,因为课后有好多的学生来找我,提问题,讨论模型。所以,我觉得,把学生自己可以学懂,能独立解决的问题放在课前,课堂上来交流我们需要帮助的难题,来提高学生对于数学的好奇心,激发学生学习数学的兴趣,鼓励他们创造解决问题的办法,我认为我们的每一节课,都应该为今后做点什么。





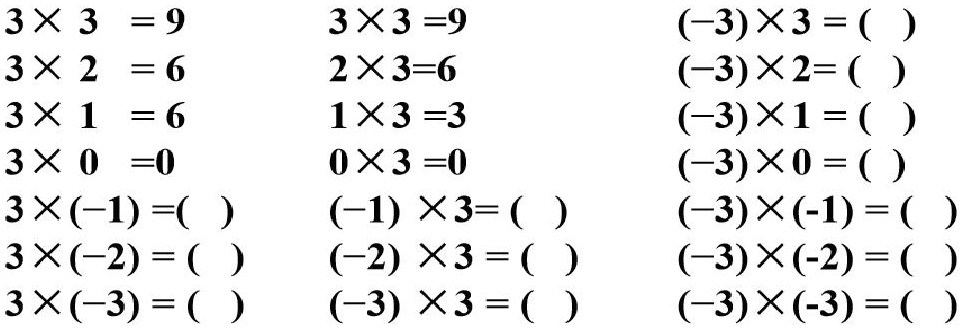

 京公网安备 11011302003690号
京公网安备 11011302003690号


