打开文本图片集

一、案例背景

高中数学，不仅是学生进一步学习数学知识的重要路径，更是培养学生抽象思维、逻辑推理、空间观念、创新意识等核心素养的关键方式。高中数学教学中，教师多关注学生是否掌握重点知识和技能，忽视学生核心素养的培养，这不利于学生深度学习和长远发展。同时，高中数学素养中，数学文化是重要组成部分，通过了解数学思想方法、数学史、数学应用意识等数学文化，不仅能够帮助学生建立完整的数学认知体系，还能够为发展学生数学核心素养提供助力。

平面解析几何是高中数学中的重要知识点，是初中阶段函数与方程知识的细化与延伸。在学习平面解析几何的过程中，学生能够逐步锻炼举一反三、触类旁通的能力，强化几何直观、空间概念、建模意识。在学习平面解析几何最短路径相关知识时，通过融入经典数学典故、数学历史，能够推动学生感知数学的魅力和精彩，还能够让学生领悟数学的转化思想，更能够让学生体会数学与生活的紧密关联，从而提高学生的数学素养，为学生以后数学学习及发展奠定坚实基础。

二、案例过程

（一）关联历史素材，激发学习兴趣

高中生面临诸多学习内容，很容易因为学习压力过大导致疲惫、厌烦等不良状态，影响学习效果。同时，高中数学知识难度加大，其中平面解析几何抽象性强，让学生容易感到枯燥、乏味。面对这种情况，在平面解析几何学习中关联历史素材，能够让学生意识到数学学科发展的源远流长，也能够打造轻松、愉悦的学习氛围，推动学生更主动投入到课堂中。

例如，在讲解最短路径问题时，阐述数学史上古希腊学者海伦解决“将军饮马”问题的故事，让学生意识到早在很多年前，学者和数学家就已经在数学领域有更多探索和成就，驱动学生积极学习数学知识。又如，在分析例题“悟空与二郎神在离地面1米的空中决斗，两人相距2米，悟空想用分身直接偷袭二郎神，为了不引起对方的警觉，分身必须在地面反弹一次再进行攻击，则分身到达二郎神的位置所走的最短距离为（ ）米。”时，融入古希腊数学家海伦（Heron of Alexandria）发现光在镜面反射中总是走最短路径，根据三角形的三边长度关系，很容易利用轴对称知识得到最短距离。同时，还融入光学研究及牛顿力学成就让拉普拉斯时期的数学家认为世界遵循严格的数学定律、以及古代数学家根据数据检验并归纳出公式的手段等内容。借助这些历史素材的融入，让学生发现数学知识在历史进程中不断被研究、传承、应用，数学家的严谨精神也在历史长河中熠熠生辉，推动学生产生探究数学知识的强烈兴趣。

（二）渗透转化思想，提高解题能力

高中学生抽象思维逐步发展，也积累的一定的数学知识，但是，学生在面临较为复杂的问题时，依然存在畏难、抵触等现象，不利于数学水平的提升。面对这种现象，在解决平面解析结合最短路径问题时渗透转化思想，引导学生结合以前所学知识找到解决问题的关键点，让学生学会举一反三、灵活转换，顺利提高学生解题能力和数学水平。

例如，在高中平面解析几何最短路径学习之前，教师首先引导学生复习以前所学“将军饮马”几何模型。在这一著名问题中，引导学生思考：唐朝诗人李顾的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河。”诗中将军在A处带马儿去河边河水，然后返回军营B处，将军怎么走路径才会最短呢？在解决这一问题中，引导学生利用轴对称、折线段转变直线段的方法解决问题，形成解决类似问题的模型，也顺利理解和应用转化思想。随后，结合这一数学模式，展示相关例题，如某公司要在长、宽、高分别为50米、40米、30米的长方体建筑的表面架设专用电路管道连接建筑物内最远两点，预设的最短管道长度介于（）米之间。结合这一最短路径问题，引导学生先解析题目中关键信息，让学生了解如果最远的两点是相对的两点，假设是AB，问题所求是最短管道长度，也就是A到B的最短距离，这就需要将长方体展开成平面图形，在计算哪种展开情况下数据最小。了解如何解题之后，教师引导学生分组展开讨论，并动手画一画、算一算，逐个计算哪个展开图最小。通过这个过程，顺利得出最后答案80-90米之间。结合学生解题过程，请学生总结类似问题的解题关键点，如采用展开放在同一平面，连线计算的方法；通过计算不仅能够得出最短路径，还能够掌握路径数。借助探究、分析、归纳总结的过程，让学生不仅解决问题，还能够提炼出解决问题的方法，从而顺利提高解决问题能力。

（三）理论联系实际，体会数学价值

数学在生活中应用十分广泛，虽然学生已经有初步认识，但是感知并不深刻。通过分析生活中的最短路径问题，能够让学生认识到学习数学知识的重要性，也能够让学生探索深层次的数学知识，从而培养学生应用意识和利用数学知识解决实际问题的能力。

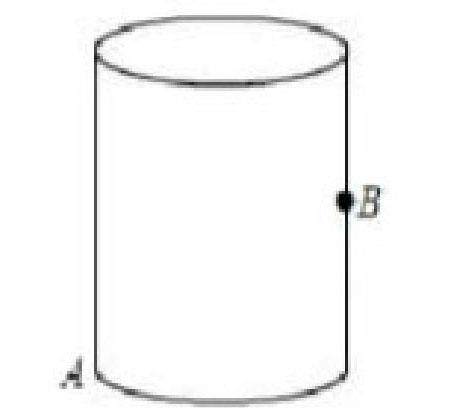
在学习平面解析几何最短路径时，教师展示生活中例题，如“火车站A和B与初始发车站C的直线距离都等于akm，站点A在发车站C的北偏东20度，站点B在发车站C的南偏东40度，若在站点A和站点B之间架设火车轨道，则最短的距离为（）”“李老师的茶杯是圆柱形，如右图是茶杯的立体图，左边下方有一只蚂蚁，从A处爬行到对面的中点B处，如果蚂蚁爬行路线最短，请画出这条最短路线图，”等，让学生在这些与生活密切相关的问题情境中，掌握最短路径相关知识。同时，教师还引导学生探索最短路径在生活中的具体应用，如快递配送中如何规划路线，找出最短路径，提高配送效率等，请学生分组合作，共同设计问题、讨论问题、解决问题，并鼓励学生利用计算机软件探究问题，提高学生的综合素质。通过探索问题的过程，让学生深入体会数学知识在生活中的广泛应用和重要价值，让学生更积极投入到数学学习中。

三、案例评析

在本案例中，通过深入挖掘与平面解析几何最短路径相关联的历史故事，引导学生感知数学发展的源远流长，体会数学的学习价值，激发学生探索数学知识奥秘的强烈兴趣，为深入学习数学知识创造有利条件。同时，在解决最短路径问题时，引导学生将未知转化为已知，利用已学知识解决复杂问题，从而感知转化的数学思想，推动学生能够应用这种数学思想更高效解决问题。另外，通过联系生活中问题，让学生体会数学在不同生活领域的应用，推动学生感知数学的实用性和价值。可见，本次案例获得了较为成功的效果，让学生从中有更多收益。