打开文本图片集

摘要：几何直观是一种通过几何图形来理解和感知数学概念、定理和策略的方法。一方面，作为一种有效的思维辅助工具，有效地联结了学生的具象思维与抽象思维；另一方面，更深入地揭示数学深层逻辑，有助于学生挖掘知识间的内在关联。本文主要是从数学概念、运算算理以及解决问题三个方面提出了几何直观教学的策略。

关键词：几何直观；核心素养；小学数学

《义务教育数学课程标准（2022年版）》（以下称为“新课标”）明确指出了小学教育阶段的核心素养，其中，几何直观作为一种关键能力，能够揭示问题的本质，明确思维的逻辑线索。曹培英也指出直观思维既是数学抽象的基石，也是强化数学认知的有效工具。同时，它构成了数学理解的核心要素，推动着数学抽象的深入理解和对数学本质的观察。考虑到小学生在生理和心理上的成长，求知欲望日益增强，抽象思维能力也在逐步发展，因此学生倾向于探究知识的生成过程而非仅停留于结果。在这种情况下，强调培养学生的几何直观能力，不仅能使抽象概念变得具象可感，还能促进学生梳理并发现知识之间的复杂关联，以此揭示数学知识点之间的内在关联。

一、几何直观在表征数学概念教学中的运用

数学家华罗庚曾言：“数缺形时少直观，形缺数时难入微。”数学学科知识点较为抽象，专注于数量关系与空间形式，导致许多小学生对数学心生畏惧。因此，小学数学教师肩负重任，需借助直观的教学方法揭示数学的“抽象”本质，将抽象的数学语言和公式具象化展现，从而使学生能感知数学的趣味性和可视化，降低学习的复杂性，进而激发学生对数学的热爱。以“最大公因数”教学为例，传统教学策略往往采取直接讲授的方式，列出两个自然数，让学生找出各自的因数。然而，此类教学方法仅使学生对“公因数”和“最大公因数”的理解停留在表面层次，对于如何寻找最大公因数，也仅仅局限于枚举法的应用。 在教授此课时，我选择了将“数”转化为“形”，通过引导学生参与动手、动口和动脑的实践活动来深化理解数学概念。

首先，展示了一张长18厘米、宽12厘米的长方形纸片，并提出问题：“若需将纸片剪切成若干相同大小的正方形且无剩余，这些小正方形的边长可能为多少？”在学生充分独立思考之后，以小组形式通过剪裁、绘制等手段进行实际操作。 在此过程中，各组给出了不同的答案：有的提议边长为1厘米，有的建议2厘米，还有人提出3厘米或6厘米。最终，全班共同讨论得出结论，即小正方形的边长可能是1厘米、2厘米、3厘米或6厘米。在学生的实践操作和思维碰撞后，我适时指出：“这些数值如1、2、3和6，都能同时被18和12整除，因此它们是18和12的公因数，其中6是最大公因数。”随后，我借助韦恩图进行可视化展示。如此，抽象的“数”得以通过具象、可操作的“形”展现，静态的数学概念转化为动态的实际操作，使得学生不仅能直观地理解数学概念，还能掌握寻找两个数的公因数和最大公因数的方法。这种“以形解数”的教学策略显著降低了数学抽象性对学生学习的挑战，通过“形”作为媒介直观地展现数学概念，有助于学生准确把握数学概念的核心含义，同时也提升了他们的几何直观能力。

二、几何直观在数学运算算理教学中的运用

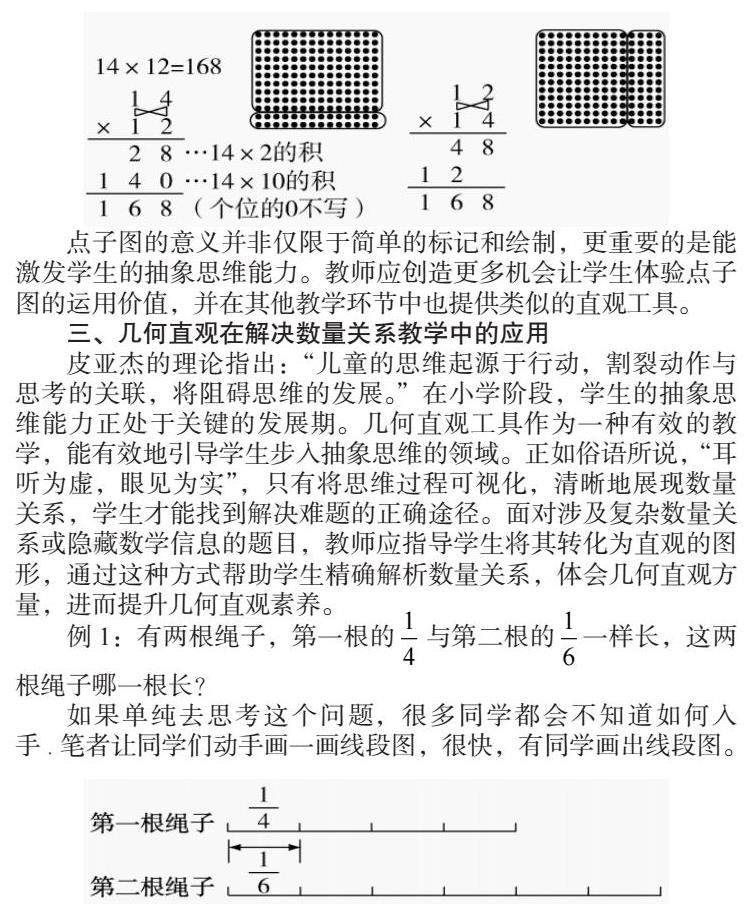
计算作为小学“数与代数”部分的核心内容，其目标不仅是使学生熟练掌握算法，更需理解其背后的数学原理。然而实践中，教师往往因急于推进教学进度而忽略了对原理的深入讲解，这可能导致学生无法理解其中的算理，进而无法真正掌握计算技巧。为解决这一问题，教师可依据具体的内容，利用相应的几何图形，以深化学生对算理的理解。比如在学习“两位数乘两位数”时，借助点子图这一几何模型，能有效阐明竖式计算的逻辑。

例1：在一场少先队员的队列展示中，排列成12行，每行包含14人。求总人数。

步骤一：教师首先引导学生形成问题意识，提出参与队列表演的少先队员总数是多少？，随后，学生将列出算式14×12或12×14。

步骤二：利用点子图探索计算策略。引导学生回顾已学习的整体分块求积法，并在点子图上进行动手操作，求解14×12（或12×14）。学生可选择先组合10个14再组合2个14，或者先组合10个12再组合4个12，以此理解计算过程。

步骤三：学生间分享在点子图上标记的过程，以及对应的算法理解。

点子图的意义并非仅限于简单的标记和绘制，更重要的是能激发学生的抽象思维能力。教师应创造更多机会让学生体验点子图的运用价值，并在其他教学环节中也提供类似的直观工具。

三、几何直观在解决数量关系教学中的应用

皮亚杰的理论指出：“儿童的思维起源于行动，割裂动作与思考的关联，将阻碍思维的发展。”在小学阶段，学生的抽象思维能力正处于关键的发展期。几何直观工具作为一种有效的教学，能有效地引导学生步入抽象思维的领域。正如俗语所说，“耳听为虚，眼见为实”，只有将思维过程可视化，清晰地展现数量关系，学生才能找到解决难题的正确途径。面对涉及复杂数量关系或隐藏数学信息的题目，教师应指导学生将其转化为直观的图形，通过这种方式帮助学生精确解析数量关系，体会几何直观方量，进而提升几何直观素养。

如果单纯去思考这个问题，很多同学都会不知道如何入手.笔者让同学们动手画一画线段图，很快，有同学画出线段图。

从图中，很直观能看出第一根绳子的长度小于第二根绳子的长度，即这两根绳子中第二根长。类似线段图是解决较复杂的应用题的重要学习工具，可以直观呈现数量关系，是有效提高学生解决问题能力的途径。

结语

总而言之，伴随着新课程改革推进，提升学生数学素养，培养几何直观素养显得至关重要。教师应当运用有效的教学策略，使学生能够直观把握数学概念、运算原理和数量关系等，努力将抽象问题转化为具象，使数学思维可见，建立直观图形与抽象知识间的桥梁，从而高效促进学生的几何直观素养发展。

参考文献

[1]丁秋平.小学数学几何直观教学的优化探析[J].教育（周刊），2021（13）：1.

[2]吴细妹.核心素养下小学数学几何直观教学改进探讨[J].教师，2019（15）：2.

[3]孙远亮.基于小学数学核心素养下的几何直观教学研究[J].数学大世界：上旬，2020（1）：1.

[4]孙承勇.谈几何直观在小学低段数学教学中的运用[J].小学教学参考，2020（3）：2.

[5]陈明悦.核心素养下小学数学几何直观实践[J].文理导航，2022（15）：3.