
- 收藏
- 加入书签
练习指向:“一核两翼三环 ”小学数学练习课教学模式的班本探索
摘要:练习课主要是以培养和训练学生对知识技能技巧掌握与运用为主要目的的一种课型。在我们的实际教学过程中,部分老师对数学新课标下练习课的教学存在困惑和问题。本文主要“从什么是练习课”,围绕“具体练习课例”,重点“阐述如何设计好一堂好的练习课”,核心思想是“一核两翼三环 ”。
关键词:练习课;一核两翼三环;模式建构;设计策略
一、对小学数学练习课教学的定位认识
有效的练习,是学生在教师指导下,独立运用所学新知、自主解决问题、不断提升素养的教与学过程,是学生对新知建构的重要实践,具有“巩固反馈、形成认知、提升能力、发展思维”的功能。
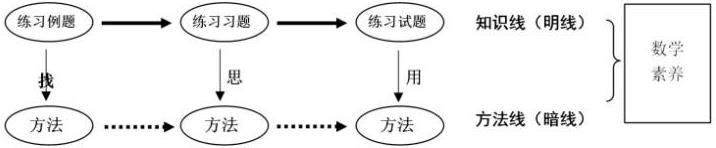
二、我班小学数学练习课教学模式的核心思想
我班尝试的练习课堂教学建构模型核心思想提炼“一核两翼三环 ”的内涵,如下图所示:
“一核两翼三环 ”的内涵,贯穿整个“教、学、练”过程,完成某一类别知识或解决某一类类问题的基本思维模式。本质上,就是学生在理解并掌握基本概念、基本结构、基本思想的基础上,利用所学知识去思考和解决问题,提高学生的数学素养,培养学生运用数学解决问题的能力。
“两翼”的内涵,指以练习例题、教材习题、补充试题等练习内容构成的知识线,此为明线;完成某一类知识或解决某一类问题,从而形成的思维方式,此为暗线,并且贯穿其中。
“三环”的内涵,指以“练习题组找方法”,“ 练习题组悟思维”、“练习题组寻策略”三个环节贯穿的“教、学、练”全过程。
三、我班小学数学练习课教学模式的任务分解
(1)明确目标(约2分钟):交流预习、明确任务、师生互动;
(2)整体把握(约10分钟):画知识线、圈点批画、问题引导、自学为主;
(3)探寻方法(约10分钟):小组讨论、归纳方法、 概括结构化、互帮互学;
(4)训练验证(约6分钟):讨论思考、总结经验、揭示规律、建构体系;
(5)检测运用(约7分钟):深化理解、当堂矫正,纠错迁移;
(6)系统深化(约5分钟):检测验收、强化记忆、整体把握。
【设计意图:在教材现有的练习内容和能力建构上,真正把练习的权力交给学生,把练习空间让给学生,把创造机会还给学生,充分体现学生精练,老师精讲,当堂训练,堂堂清。】
四、我班小学数学练习课教学模式的策略探索
1、明确目标,激发参与
练习课伊始,通过师生间的亲切对话、回归生活、自主参与、价值导向、走向成功等练习情境,激发学生求知和探索兴趣,调动学生参与练习的积极性,让练习课为学生的素养提升保驾护航。
例:出示:学校图书室为六年级(1)班35人,六年级(2)班32人 ,六年级(3)班34人购买了303本文学读物,开展书香班级活动,平均每个班分得多少本?
生上台展示:303÷3=101(本)
写对的同学举手核对,教师出示答语并齐读:
分析与讨论:
班级人多人少,分到一样多的本书,不太合理。怎么办解决这个问题?(按班级人数的比例分配)
2、启发回顾,巩固基础
教师引领学生对基础练习题中的新知识、新方法,通过观察、操作、归纳、交流、辨析等途径进行巩固,通过师生交流,厘清楚双基重难点,为后续学习搭好台阶。形成性练习,教师因材施教,分层教学,实现学生练习后的自我内化,每一个学生基础能得以巩固、能力获得强化,让每一个学生都有成功的自豪感。
例:学生独立解决:
学生评议:(1)人多的班级分的多,人少的班级分的少,比较合理。
(2)三个班每人都可以分到三本书,学生们都满意了。
3、比较分析,强化认识。
有效实施练习,教师充分发挥练习指路人的作用,通过对题组的设计,让学生在对比中明析知识体系的本质,增强学生灵活运用能力;通过对题组的探究,让学生触类旁通,抽象概括出自己的发现;通过师生题组间的交流对话,提升学生的练习水平。
例:六(4)班和六(5)班争创科技特色班级,学校给六(4)班购买了90本科普图书,与六(5)班本数的比是5:4,六(5)班分得多少本科普图书?
比较分析:
90本 → ?份
认识归纳:
单个量(六(4)本数)→5份(六(4)分得的份数)
比较方法:
90÷5×4=72(本)
六(6)班和六(7)班分到本数的比是4:3,六(6)班比六(7)多分得30本,两个班各分得多少本图书?
讨论思考:
90本 → ?份
探索深化:
相差量(多分得30本)→(4-3)份(多分得1份)
巩固迁移:
30÷(4-3)× 4=120(本)……六(6)班本书
30÷(4-3)×3=90(本) ……六(7)班本书
5、当堂反馈,小结反思
在课堂总结阶段,可以设计适当的检测性练习题,让学生独立进行练习,达到及时反馈与矫正的目的,引导学生自觉参与课堂评价,如:对本节练习课的综合表现、练习总体达成情况等进行自我总结与反思,体验挑战练习快乐与成功。
例:
(1)隐含总量
一个三角形的三个内角度数的比分别是2:3:5,这个三角形的三个内角各是多少度?
(2)重新分配总量
一个长方形的周长是108厘米,长与宽的比分别是4:5,它的面积是多少平方厘米?
(3)隐含分量所占的份数
一个等腰三角形的周长是54厘米,腰与底的比分别是2:5,它的三条边各是多少?
【设计意图:在练习教学过程中,要瞄准教学的重难点,精心设计有层次、有坡度,有冲突的变式练习题。让学生在不断的练习冲突中,渐渐摸索处解决问题的策略,使思维的发散性、灵活性得到深刻发展。】
综上所述,面对新数学课程标准的来临,怎样上好一节令人向往的小学数学练习课,是摆在我们广大一线数学教师面前的一项重要任务。提高练习课的价值,向练习课要效益,以学生为本精心设计练习内容,扎根于“属于儿童的练习场”,努力发展学生的数学素养,上出具有数学标向的练习课。





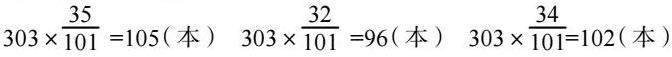

 京公网安备 11011302003690号
京公网安备 11011302003690号


