摘要：探究式学习是高中数学教学改革的重要方向。文章基于问题驱动的理念，对高中数学探究式学习的模式设计与实施策略进行了系统阐述。介绍了基于数学核心概念设计问题情境、借助信息技术平台实施个性化指导、开展探究成果交流与评价三个关键环节的策略。研究表明，在问题驱动和师生互动中，学生经历知识生成的完整过程，内化探究方法，发展元认知，有助于提升数学核心素养。

关键词：高中数学；探究式学习；问题驱动；教学设计

引言：数学是一门基于抽象和逻辑的学科，培养学生的数学核心素养是高中数学教育的重要使命。新课标明确提出，要通过数学探究等学习方式，促进学生全面而有个性地发展。当前，问题导向、主动建构等学习理念日益受到重视，探究式学习逐渐成为高中数学教学改革的重要方向。然而，如何立足问题驱动的理念，优化探究式学习的模式设计与实施策略，仍需要理论探讨与实践探索。

一、基于核心概念设计问题情境，突出数学本质

数学核心概念凝结了学科知识体系的基本要素，蕴含了丰富的数学思想和方法。教师应立足课程标准和教材，系统梳理每个单元的核心概念，围绕这些概念精心设计问题情境，引导学生探索概念形成和发展的逻辑脉络，感悟数学的抽象性、整体性和严谨性等本质特征[1]。同时，问题情境要贴近学生已有的认知基础和生活经验，激发学生的探究兴趣，促进知识的内化和迁移，培养学生运用数学理解和解决现实问题的意识与能力。

以高一《等式性质与不等式性质》为例，等式的传递性、不等式的传递性等性质是本节的核心概念。教师可设计如下探究情境:已知函数f(x)在其定义域上恒大于 0，函数g(x)在其定义域上恒小于 0，探究 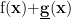与0 的大小关系。教师引导学生运用等式的传递性、不等式的传递性等性质，通过逻辑推理得出 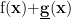的取值范围，深化对函数与不等式之间内在联系的理解。在探究过程中，学生不仅掌握了等式和不等式的基本性质及运算法则，还能感悟数学语言的简洁和数学推理的严密性。进一步，教师可引导学生探究参数不等式的解集问题，如讨论 K 的取值范围，使得不等式组 {x+1<2K,2x-1>K} 有解。学生需要运用不等式的性质进行转变和逻辑推理，通过对参数K 的连续取值，探寻问题结构的动态变化，理解不等式解的连续性和参数不等式的本质，这对于培养学生的逻辑思维能力和数形结合思想具有重要意义。学生还可尝试利用等式与不等式的性质解决一些实际问题，如经济利润最大化、工程造价优化等，体会数学的应用价值。

教师应立足数学核心概念设计问题情境，引导学生在主动探究中经历概念的形成过程，体验数学抽象、逻辑、联系等核心素养。这对于改进传统“题海战术”、提升数学课堂教学质量具有积极的借鉴价值。

二、借助信息技术平台，实施个性化的探究指导

借助信息技术平台，实施个性化的探究指导，是开展高中数学探究式学习的有效策略。信息技术为学生的探究学习提供了丰富的资源支持和便捷的交互方式，教师应充分利用信息技术平台，为学生营造一个自主探究、合作交流的学习环境。在此基础上，教师要根据学生的个体差异，提供多层次、多角度的问题情境，嵌入恰当的学习支架和提示信息，引导学生开展个性化的探究活动。同时，教师要利用平台的数据分析功能，即时跟踪学生的探究进程，精准诊断学生在探究中遇到的困难和问题，提供适切的指导和反馈，促进学生探究能力的持续提升。

以《函数的基本性质》为例，教师可在信息技术平台上创建一个“函数探究专题”，设置一系列问题情境，引导学生探究函数的单调性、奇偶性、周期性等基本性质。如在研究二次函数 y=ax²+bx+c(a≠0) 的性质时，平台根据学生已有的认知水平，动态呈现不同参数a、b、c 取值下函数图像的变化情况，启发学生探究参数与函数图像之间的内在联系。学生可通过交互式操作，动态观察图像的位置、开口方向等变化规律，提出合理猜想，再通过演绎推理加以验证，深化对二次函数性质的理解。对于探究能力较强的学生，教师可进一步设置开放性问题，如“对于怎样的二次函数，存在 x1≠x2 ，使得f(x1)=f(x2)? ”学生需要运用所学的函数性质，通过逻辑论证得出结论，并尝试构造满足条件的二次函数，提升数学抽象和逆向思维能力。对于探究过程中遇到困难的学生，教师则可根据平台数据反馈，提供个性化的启发与指导，如引导学生回顾二次函数图像与一元二次方程根的关系，透过图像理解问题的本质。通过探究活动的开展，学生不仅掌握了二次函数的基本性质，更加深了对函数这一核心概念的理解，提升了运用函数的观点和方法分析、解决问题的能力。在问题驱动和教师引导下，学生通过主动探究，经历知识生成的完整过程，习得数学概念背后的本质理念，提升探究能力和创新意识。

三、开展探究成果交流与评价，发展元认知能力

探究成果的交流与评价不应局限于结果的呈现，更应关注探究过程的反思与优化。教师应创设多样化的交流情境，引导学生用数学语言阐释思路，评判方法的优劣，分析探究过程中遇到的困难和应对策略，培养学生自我监控、自我调节的元认知能力[2]。同时，教师要本着述而不评、启发诱导的原则，引导学生开展同伴互评和自我评价，促进学生在交流碰撞中彼此启发，在反思评价中不断修正完善，提升数学交流能力和批判性思维能力。

以高一《三角函数的图象与性质》为例，在学生探究正弦函数、余弦函数、正切函数等三角函数的图象和性质后，教师可组织一次以“特殊角三角函数图象”为主题的交流活动。学生以小组为单位，围绕“ 0^∘ 、 30^∘ 、 45^∘ 、 60^∘ 、 90^∘ 等特殊角的三角函数值如何快速确定”“为什么正弦函数和余弦函数的图象关于 y=x 对称”“为什么在 x∈Γ(0) π/2 ）时，正切函数单调递增”等问题展开讨论。小组成员通过头脑风暴、思维导图等方式，梳理各自的探究思路，交流不同解题方案的异同，评析方法的优劣。如在讨论“正切函数的单调性”时，有的学生可能从函数解析式入手，利用导数判断；有的学生则可能借助几何意义，通过三角形相似得出结论。教师则可引导学生比较两种方法的特点和局限，启发学生从问题的表象深入本质，探寻数形结合的内在逻辑。在交流过程中，学生还要反思探究中遇到的困惑，如“为什么同角的正弦、余弦值平方和恒为 1”“锐角三角函数表中角度如何拓展到任意角”等，分享克服困难的心路历程。教师则适时引入“元认知”的概念，帮助学生总结探究的思维过程，优化探究路径，提升后设认知能力。通过探究成果的系统梳理、精要提炼、深度反思，学生在掌握运用三角函数知识解决问题的同时，更加深刻地理解了数学探究的一般过程，内化了科学探究的基本思想。

结束语

高中数学探究式学习是深化课程改革，培养学生创新精神和实践能力的有效途径。实施探究式学习，需要教师立足数学学科核心素养，精心设计问题情境，借助信息技术手段，为学生提供个性化的探究指导，开展探究成果交流与评价，发展学生的元认知能力。这是一个系统优化、协同促进的过程，对于推动教与学方式的变革，提升学生的数学核心素养具有重要意义。在未来的教学实践中，教师应立足国家课程标准，紧扣学生身心发展规律，整合多方资源，不断创新探究式学习的模式，为学生全面而有个性地发展提供丰富的土壤。

参考文献：

[1]张超,朱宸材.真实问题情境下的项目式学习探究——以"最小覆盖圆"为例[J].中学数学教学, 2024(3):10-14.

[2]贤萍萍,刘媚.基于问题驱动提高数学学科素养的案例探究--以"变化率问题"为例[J].数理化解题研究, 2023(12):35-37.