打开文本图片集

摘要：测量性实验是初中物理实验的重要组成部分，学生需要在实践过程中掌握测量器材的正确使用方法，并学会减小实验误差的一般性思路。本文分析了“用刻度尺测量纸张厚度”实验中存在的问题，并对实验改进的原因和方法进行了阐述。

关键词：累积法；多次测量求平均值；误差分析；深度学习

义务教育物理课程标准的内容框架中，一级主题“实验探究”由两个二级主题构成，分别是“测量类学生必做实验”和“探究类学生必做实验”，两类实验相互关联，各有侧重。其中测量类实验需要学生掌握测量工具的科学使用方法，能够解决生活实际问题，培养学生动手操作和收集数据的能力、分析和处理数据的能力，培养学生严谨认真、实事求是的科学态度。由于测量过程中的误差不可避免，因此，误差分析也成为优化测量性实验的重要环节。初中阶段，对学生而言，误差分析的要求并不高，更多的是定性分析，了解测量误差形成的原因、掌握减小实验误差的方法。但对于教师而言，应该用更为专业、深刻的眼光，聚焦实验数据，以定量分析激发科学思维，引领学生真正掌握科学减小实验误差的方法。下面，就“用刻度尺测量纸张厚度”这一实验的常见问题，谈一谈改进的建议。

一、基于课标的内涵分析

苏科版义务教育课程标准实验教科书物理８年级上册“长度和时间的测量”一节安排了这样一个活动：

（１）想一想：如何测出一张纸的厚度？与同学交流，确定自己的测量方法。

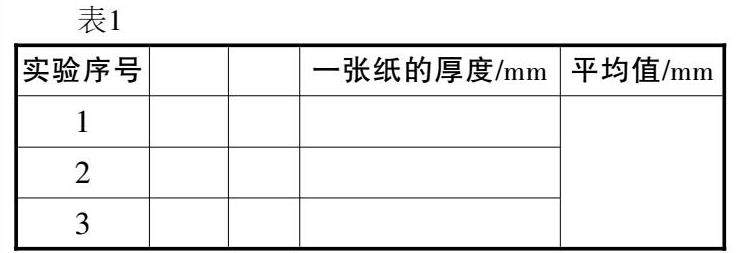
（２）做一做：把测量值填入表1中。

（３）议一议：在测量的过程中，你每次的测量结果都一样吗？与同学交流、讨论一下，为什么会出现这种情况？

“用刻度尺测量长度”是课标中９个学生必做的测量性实验之一。虽然，课标要求上并没有对“误差分析”有专门的提及，但从测量性实验的完整性而言，减小误差是体现学生学科素养的关键能力。从教科书规划的内容来看，以真实情境为依托，希望学生在解决真实问题的过程中认识“误差”的存在，并掌握用累积法和多次测量求平均值的方法来减少实验的误差。所以，刻度尺的规范使用是本实验的基础，累积法和多次测量求平均值的方法应用才是本实验的核心。

二、基于实际的问题呈现

从学生实际实验的过程来看，大致呈现以下两种不同的实验范式：

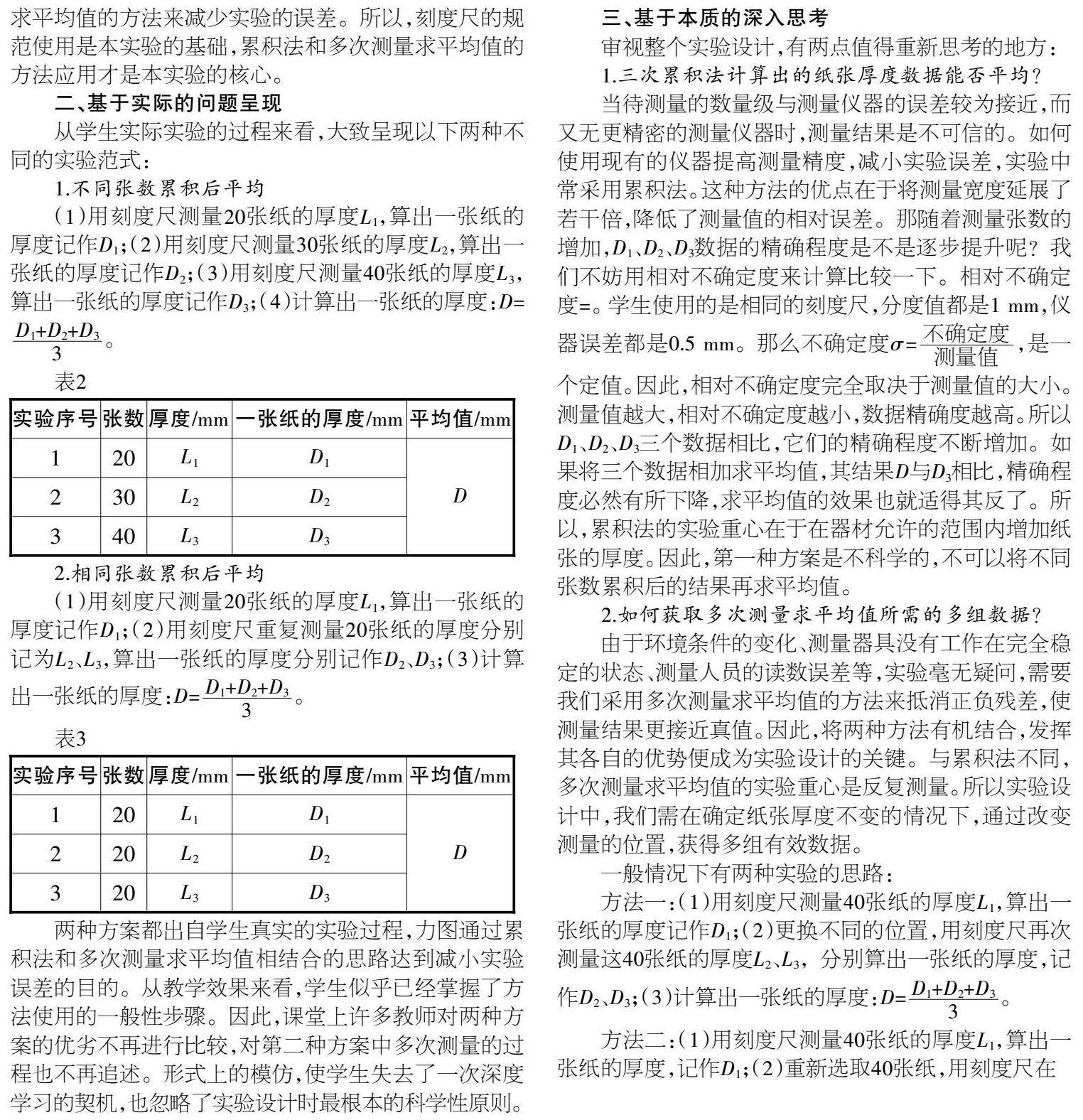
１．不同张数累积后平均

（１）用刻度尺测量２０张纸的厚度Ｌ１，算出一张纸的厚度记作Ｄ１；（２）用刻度尺测量３０张纸的厚度Ｌ２，算出一张纸的厚度记作Ｄ２；（３）用刻度尺测量４０张纸的厚度Ｌ３，算出一张纸的厚度记作Ｄ３；（４）计算出一张纸的厚度：Ｄ＝。

２．相同张数累积后平均

（１）用刻度尺测量２０张纸的厚度Ｌ１，算出一张纸的厚度记作Ｄ１；（２）用刻度尺重复测量２０张纸的厚度分别记为Ｌ２、Ｌ３，算出一张纸的厚度分别记作Ｄ２、Ｄ３；（３）计算出一张纸的厚度：Ｄ＝。

两种方案都出自学生真实的实验过程，力图通过累积法和多次测量求平均值相结合的思路达到减小实验误差的目的。从教学效果来看，学生似乎已经掌握了方法使用的一般性步骤。因此，课堂上许多教师对两种方案的优劣不再进行比较，对第二种方案中多次测量的过程也不再追述。形式上的模仿，使学生失去了一次深度学习的契机，也忽略了实验设计时最根本的科学性原则。

三、基于本质的深入思考

审视整个实验设计，有两点值得重新思考的地方：

１．三次累积法计算出的纸张厚度数据能否平均？

当待测量的数量级与测量仪器的误差较为接近，而又无更精密的测量仪器时，测量结果是不可信的。如何使用现有的仪器提高测量精度，减小实验误差，实验中常采用累积法。这种方法的优点在于将测量宽度延展了若干倍，降低了测量值的相对误差。那随着测量张数的增加，Ｄ１、Ｄ２、Ｄ３数据的精确程度是不是逐步提升呢？我们不妨用相对不确定度来计算比较一下。相对不确定度＝。学生使用的是相同的刻度尺，分度值都是１ ｍｍ，仪器误差都是０．５ ｍｍ。那么不确定度σ＝，是一个定值。因此，相对不确定度完全取决于测量值的大小。测量值越大，相对不确定度越小，数据精确度越高。所以Ｄ１、Ｄ２、Ｄ３三个数据相比，它们的精确程度不断增加。如果将三个数据相加求平均值，其结果Ｄ与Ｄ３相比，精确程度必然有所下降，求平均值的效果也就适得其反了。所以，累积法的实验重心在于在器材允许的范围内增加纸张的厚度。因此，第一种方案是不科学的，不可以将不同张数累积后的结果再求平均值。

２．如何获取多次测量求平均值所需的多组数据？

由于环境条件的变化、测量器具没有工作在完全稳定的状态、测量人员的读数误差等，实验毫无疑问，需要我们采用多次测量求平均值的方法来抵消正负残差，使测量结果更接近真值。因此，将两种方法有机结合，发挥其各自的优势便成为实验设计的关键。与累积法不同，多次测量求平均值的实验重心是反复测量。所以实验设计中，我们需在确定纸张厚度不变的情况下，通过改变测量的位置，获得多组有效数据。

一般情况下有两种实验的思路：

方法一：（１）用刻度尺测量４０张纸的厚度Ｌ１，算出一张纸的厚度记作Ｄ１；（２）更换不同的位置，用刻度尺再次测量这４０张纸的厚度Ｌ２、Ｌ３，分别算出一张纸的厚度，记作Ｄ２、Ｄ３；（３）计算出一张纸的厚度：Ｄ＝。

方法二：（１）用刻度尺测量４０张纸的厚度Ｌ１，算出一张纸的厚度，记作Ｄ１；（２）重新选取４０张纸，用刻度尺在任意位置测量其厚度Ｌ２，算出一张纸的厚度，记作Ｄ２；（３）重复以上实验，算出一张纸的厚度，记作Ｄ３；（４）计算出一张纸的厚度：Ｄ＝。

这就需要教师不仅关注实验的结果，更需要关注实验的过程，学生重复测量后的数据是否有效，是多次测量求平均值方法的关键。

可见，不同的物理方法解决不同类型的实验误差。在选择方法时，我们要对误差产生的原因有翔实的认识。对于物理方法的使用，不能只注重形似，只有真正理解其方法的内涵，才能在实验过程中做到科学合理的应用。新的课程标准的颁布，体现了物理教学从知识立意向素养立意的转变，其中很关键的一点就是我们要将素养立意融入日常教学过程。不仅要培养学生的物理自然观，而且要培养学生的科学思维习惯、科学探究能力、科学态度与社会责任，以更高远的价值追求引领学生全面发展。

参考文献：

［１］吴石林．误差分析与数据处理［Ｍ］．清华大学出版社，２０１０．８．

［２］义务教育物理课程标准（２０２２年版）［Ｍ］．北京师范大学出版社，２０２２．４．

［３］中学物理教学概论［Ｍ］．北京：高等教育出版社，２００３．３．

［４］蒋新．刍议初中物理实验中的测量误差［Ｊ］．湖南中学物理，２０２２（４）．