打开文本图片集

人类的祖先在实践中发现，不同粗细的圆木，用绳子绕上一圈，绳子的长度总是圆木直径的3倍多一点。

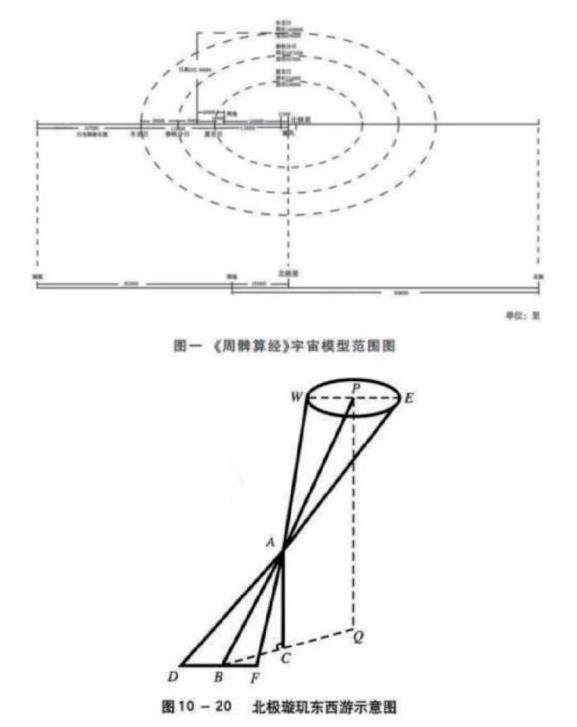
在我国，现存有关圆周率的最早相关文章是2000多年前的《周髀算经》。“周”是一个地名，“髀”是指立木测影。同学们之前在科学中学过天文方面的知识，知道观测天气要定点、定时、长期观测，也学过日晷，就是测量影子的，从书名能知道，《周髀算经》是一本关于天文计算方面的古书。《周髀算经》有上下两卷，共70章，内容丰富，艰深。

比如：“候勾六尺，……从髀至日下六万里，而髀无影。从此以上至日，则八万里。……”

“候”就是等到，“勾”，就是“勾股弦”的“勾”，直角三角形中的短边。

这段话的大概意思是“等到勾边的影长为六尺的时候，使得弦边为10尺，那么股边为八尺。”再用相似的原理算出太阳高度。

《周髀算经》中有大量的天体运行轨迹的计算。天体的运行轨迹是圆形或者是椭圆形，计算要用到圆周率。

比如：“正极之所游，冬至日加酉之时，立八尺表，以绳系表颠，希望北极中天大星，引绳致地而识之；又到旦明，日加卯之时，复引绳希望之，首及绳致地而识其两端，相去二尺三寸，故东西极两万三千里。”……“何以知南北极之时？……其两端相去正东西，中折之以指表，正南北”。“冬至夜半北游所极夜……以夏至南游所极。此皆以绳系表颠而希望之，北极至地所识丈一尺四寸半，……其南极至地所识九尺一寸半，”

通过复验这些数据，可以知道《周髀算经》使用的圆周率的大小。

在三国、唐朝的古代学者对书中的计算进行注解：三国时，赵爽注解：“圆径一而周三。”

唐朝的杨炯注解：“周三径一”。

我国古代数学经典书籍《九章算术》在第一章“方田”中写到“半周半径相乘得积步”，也就是我们现在说的s=r²π。

我国魏晋时期数学家刘徽，读到这里，为了证明这个公式，公元263年撰写《九章算术注》，在这一公式后面写了一篇1800余字的注记，这篇注记就是数学史上著名的“割圆术”。

刘徽用这种方法不断地“割圆”，一直算到圆内接正192边形，得到圆周率的近似值是3.14.

根据《隋书·律历志》关于圆周率（π）的记载：“宋末，南徐州从事史祖冲之，更开密法，以圆径一亿为一丈，圆周盈数三丈一尺四寸一分五厘九毫二秒七忽，朒（nǜ）数三丈一尺四寸一分五厘九毫二秒六忽，正数在盈朒二限之间。密率，圆径一百一十三，圆周三百五十五。约率，圆径七，周二十二。”

这段话的意思是：祖冲之把圆的直径当作单位"1"，周长，最大是3.1415927，最小是3.1415926。用分数表示，不精确的值为22/7，精确的值为355/113。

这就厉害了！这一成就，在当时是世界上的最高水平，一直到900多年中，都是世界第一，没有其他国家能超过他。

直至15世纪阿尔.卡西算到圆周率3.14159265358979325，有17位准确数字，这才打破了祖冲之保持了900多年的记录。

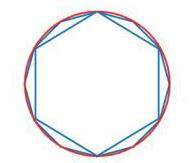
国外早的计算圆周率的人，算是公元前三世纪的希腊数学家阿基米德了。他发现了：当正多边形的边数增加时，它的形状就越来越接近圆。

他得出的结论是：圆周率约223/71，近似为22/7。

现在，人们用计算机计算圆周率，2000年，圆周率已经可以计算到小数点后12411亿位。

据网络报道，最近，科学家通过超级计算机，耗时三个半月，把圆周率的小数位算到了62.8万亿位，人类获得了史上最为精确的圆周率。

我们平时在生活中基本上只要用到圆周率小数位的前两位，普通工程上取前五位也够用了。既然如此，为什么还要不断计算圆周率？能算到尽头吗？

圆周率是一个无限不循环的小数，也是超越数。

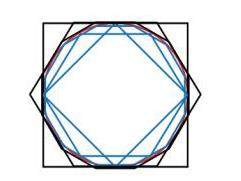
不过，从算术上想，如果把正方形周长作为单位1，那么它的内接圆的周长是“π/4”，内接圆的周长是无限不循环小数；反过来，如果把圆的周长作为单位1，那么它的外接正方形的周长是“4/π”，此时无限不循环的小数是正方形周长了。