打开文本图片集

摘要： 随着城市化进程的加快，道路交通拥堵问题日益严重，成为影响城市经济发展和居民生活的重要难题，优化城市交叉路口的信号控制方案对于提高城市交通效率具有重要意义。首先，信号配时的原理是将交叉口所具备的时间资源根据各流向的交通量的按比例分配给各流向，因而信号配时的关键就在于确定最佳的周期长度，其次，周期和绿信比是信号配时的两个最重要的参数，信号配时优化就是对交叉口信号周期和绿信比的优化，最后确定以车辆延误时间最小为目标的函数，基于Webster算法设计信号灯配时方案，求出使目标函数达到最优的相位方案、周期时间和最小损失时间。最终通过MWORKS求解最优配时，得到四个时段的最优信号周期总和分别为19.03秒、63.55秒、57.46秒、26.98秒，最小损失时间分别为13.3367秒、35.2012秒、31.945秒、17.211秒。

关键词：绿信比 信号周期 Webster配时 MWORKS

一、引言

通过分析各路口在不同时段的交通流量数据对道路交叉口的信号灯进行配时优化，使车辆的平均速度达到最大化。目前在交通信号配时方面主要有人工指挥法、固定配时法和Webster配时法，这些方法在解决交通拥堵方面效率不高或人工成本高，并不能解决实际问题。因此需要同时考虑信号配时和环境才能得出最优的信号配时方案，达到车流平均速度最大化。要对道路的交叉口的信号灯进行了配时优化。目的是使主路上车辆的平均速度最大化，减少红绿灯对通行效率的损耗，首先通过绿信比公式确定了不同时段和不同方向的交通时间比例。根据信号周期公式，计算得出车辆在四种行驶模式下的信号周期总和，最终代入Webster配时法公式。

二、模型假设

为了建立更精确的数学模型，本文根据实际情况建立一些合理的假设和条件约束。

假设：

（1）所有车辆都遵守交通规则，即不闯红灯。

（2）不考虑车辆行驶过程中发生交通事故的可能性。·

（3）不考虑路面施工造成交通拥堵的情况。

（4）不考虑路面积雪、积水、结冰等现象对车辆的影响。

（5）不考虑信号灯会出现损坏情况。

（6）设经中路-经纬路四个方向各有一个摄像头记录车辆通行。

三、符号说明

四、利用Webster配时法优化道路信号配时

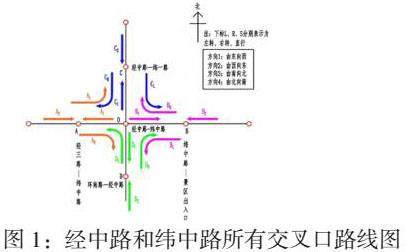
对路口的各个出口和各车流方向进行编号，如图1所示：

根据该路口的各个出口的车流量数据，对经中路和纬中路所有出口进行信号灯配时，车辆经过经过交叉路口时有四种行驶模式，车辆行驶模式如图2所示：

基于图2的4种汽车行驶模式，为使车辆在通过路口时平均速度达到最大，则需要合理分配信号灯的时间，绿信比公式见式（1）、信号周期见式（2）：

式（6）中，数据代入式（6）可得各时段的信号周期与损失时间表，见表1：

由表1可知，上班高峰期和晚高峰的信号周期较长，因为此时交通流量较大，分配更多的绿灯时间以缓解交通拥堵的问题，使得两条主路上的车流平均速度最大。

五、结论

综上所述，Webster配时法用来缓解道路交通拥堵问题效果较为显著，可以应用于多种复杂的、流量大的交通路口的情形，使车辆的平均速度最大化，减少红绿灯对通行效率的损耗，能够有效地提升路口的通行能力。