打开文本图片集

关键词： 聚类、相关性分析、蔬菜销售

摘要： 生鲜商超通过销售数据监控各类商品的销售情况，了解商品的热销程度和库存变动情况。为了解蔬菜各品类及单品销售量的分布规律以及相互关系，本文应用了聚类分析的方法，首先对总销量进行去量纲处理，然后分别计算pearson相关系数与spearman相关系数，并做矩阵散点图来判断各影响因素之间是否具有线性关系，最后对各指标进行聚类，得出谱系图，对蔬菜进行分类，得出蔬菜各品类及单品销售量的分布规律。

1.引言

近年来，蔬菜销售在食品行业扮演着至关重要的角色。蔬菜类商品不同品类或不同单品之间存在一定的关联关系，主要是由于它们在供应链中的相互影响和市场需求的变化。供应链影响主要体现在一些蔬菜可能是相互依赖的[1-2]，因为它们在生长环境、生产季节和供应源上存在共性。例如，土豆、洋葱和胡萝卜是一些常见的根茎类蔬菜，它们的种植季节和供应源通常较为相似，因此它们之间的价格和供应关系会有一定的关联性。蔬菜类商品的市场需求受到季节性、健康意识和消费习惯等市场需求变化因素的影响。例如，夏季时人们对水果和绿叶蔬菜的需求较大，而冬季时对根茎类蔬菜的需求较高。因此，这些蔬菜的价格和供应也会受到季节变化的影响，根据市场需求的波动，它们之间的价格会发生变化[3-4]。

综上所述，蔬菜类商品之间存在一定的关联关系，主要是由于供应链影响和市场需求的变化，我们需要分析蔬菜各品类及单品销售量的分布规律及相互关系[5-6]。本文数据来自于http：//www.mcm.edu.cn/

2.聚类与相关性分析

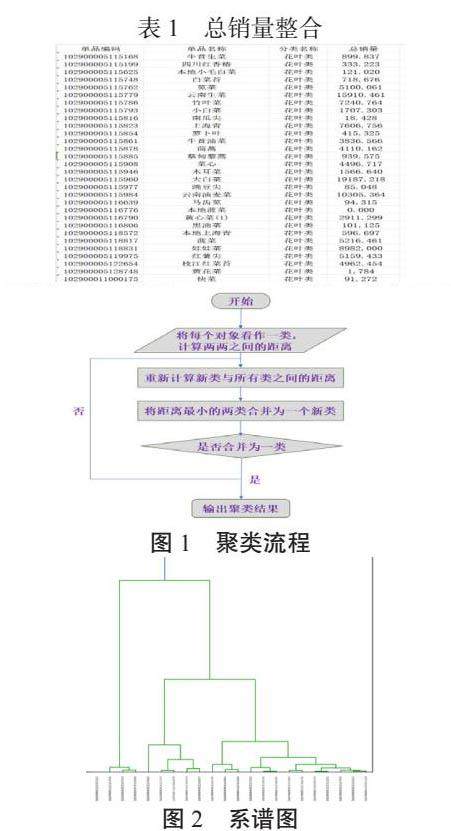
将蔬菜品类对应的总销量和蔬菜单品的总销量整合得到下表1：

为消除量纲影响，采用mean-max标准化的方法对总销量进行去量纲归一化处理。

对于不同类型变量的相关性进行初步判断。分别计算pearson系数与spearman系数并作正态Q-Q图进行判断。

通过验证，可得出本题的因素不具有线性关系且与spearman相关系数分析不适配。

最后，建立k-means聚类分析模型。具体步骤如下图1所示：

首先将单品编码与总销量作为系统聚类依据，将数据带入Python，得到谱系图如下图2所示：

其次对聚类效果进行衡量。使用sklearn库中的silhouette_score calinski_harabasz_score函数分别计算了聚类结果的轮廓系数和Calinski-Harabasz指数。得到聚类结果的轮廓系数为： 0.8196158724451897，聚类结果的Calinski-Harabasz指数为：835.9616842362583。

根据给出的聚类结果的轮廓系数和Calinski-Harabasz指数，可以初步评估聚类的效果较好。轮廓系数为0.8196，接近1。由于较高的轮廓系数意味着聚类结果的紧密性较好，故而聚类结果中的样本点相对于其所在的簇来说，更接近同一簇内的其他样本，而与其他簇中的样本相比较远。表示样本在自己的簇内部密集而不同簇之间距离较远。

Calinski-Harabasz指数为835.9617。由于较大的值表示簇内部的差异性大、簇间的差异性小，故而本聚类结果中不同簇之间的差异较大，而同一簇内的样本相似度较高。

最后根据谱系图将蔬菜划分为三类。第一类为大白菜，云南油麦菜，娃娃菜，云南生菜（份），云南油麦菜（份），奶白菜（份），黄白菜（2），西兰花，青梗散花，净藕（1），紫茄子（2），泡泡椒（精品），螺丝椒，芜湖青椒（1），小米椒（份），螺丝椒（份），金针菇（盒），这一类的销售额较大，说明该类蔬菜需求量大，分为家常常用菜类。第二类为云南生菜，竹叶菜，上海青。这一类无明显规律，分为其他类。第三类为其余种类蔬菜，该类菜品普遍销售量较低，因此归于非家常常用类。

结论

本研究旨在解析蔬菜销售量的分布规律，应用聚类和相关性分析的方法，探究不同品类及单品之间的关联，为了更好理解这些商品在市场中的交互作用。研究通过总销量的标准化，计算Pearson和Spearman相关系数，并绘制矩阵散点图以判断不同因素间的线性关系。最终，利用聚类方法对指标进行分类，并得出了蔬菜销售量的分布规律。

蔬菜销售作为食品行业中的关键因素，受供应链影响和市场需求变化的影响。各种蔬菜可能因季节、健康意识和消费习惯而相互影响，形成一定的相关性。该研究采用K-means聚类方法，将蔬菜划分为三类。第一类为销售额较大的家常常用菜类，如大白菜、西兰花等。第二类为无明显规律的其他类蔬菜，包括云南生菜、竹叶菜等。第三类则为非家常常用类，销售量较低的蔬菜。

通过轮廓系数和Calinski-Harabasz指数的评估，研究结果显示了较好的聚类效果，有助于揭示蔬菜销售量的规律和分类。.

参考文献

[1]Kaufman， L.， & Rousseeuw， P. （1990）. Finding groups in data： An introduction to cluster analysis. John Wiley & Sons.

[2]Box， G. E. P.， Jenkins， G. M.， & Reinsel， G. C. （2015）. Time series analysis： forecasting and control. John Wiley & Sons.

[3]Brockwell， P. J.， & Davis， R. A. （2016）. Introduction to time series and forecasting. Springer.

[4]Enders， W. （2014）. Applied econometric time series. John Wiley & Sons.

[5]Moscardi， E.， de-Magistris， T.， & Gracia， A. （2017）. Price strategies for fresh vegetables in traditional and modern retail outlets： The case of Spain. Food Policy， 73， 54-67.

[6]Dong， L.， Mitchell， J.， & Liu， Y. （2017）. Predicting Chinese fresh vegetable prices using online data with an ARIMA model. Agricultural Economics， 48（6）， 637-647.