
- 收藏
- 加入书签
基于几何特征寿命分布机械零件服役可靠性研究
摘要:由于制造加工工艺精密化程度变高,产品质量可靠性逐步提高,通过模拟其失效试验来获得产品失效变得更加困难,通过建立产品关键零件的退化特征量与关键质量特征之间的关系,根据质量特征的概率分布形式,获得产品的服役可靠性曲线。通过实测数据分析得到产品寿命的集中分布范围,建立基于几何质量特征寿命分布概率密度函数,然后进行产品的可靠性分析。这种通过服役质量损失与产品可靠性之间关系的方法,使研究机械零件的服役可靠性更加经济便捷。
关键词:几何质量特征;质量损失;服役可靠性
0 引言
机械零件可靠性对保证机械使用寿命和使用质量至关重要。以Haugen为代表,在应力与强度服从正态分布、相互干涉的假设下,进行了齿轮强度可靠性的设计计算。基于复杂网络理论,Yin等从可靠性的角度提出了影响部件的识别方法。此外,Chen等人提出了一种多属性可靠性分配方法。随着机械产品加工工艺的精密化,产品的可靠性也越来越高,一些加速破坏试验估计可靠性的方法对于那些大型装备实施成本太高。因此可以建立产品的退化特征量与其关键质量特征之间的关系,通过质量损失的变化规律来进行机械产品的可靠性分析会更加经济便捷。
1 产品服役质量损失分析
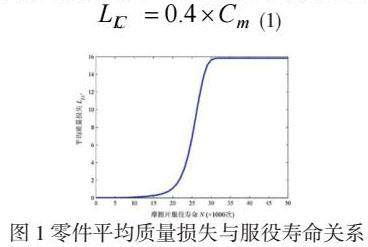
本文以某机械产品关键零件为例计算服役过程中的质量损失。机械零件之间存在摩擦间隙,零件在服役一段时间后,其间隙不断增大,从而影响使用性能,最终影响产品的性能。设ax为该零件关键质量特征,计算零件服役阶段质量损失。零件的关键质量特征和公差为。因此,△=0.1mm,Tx=3.2mm,TL=3.1mm,TU=3.3mm。零件报废的损失现值为Cm=200, 即为零件价格,N表示零件实时结合次数。已知零件关键质量特征分布参数μx=3.19765mm,σx=0.015269mm,在服役参数α=-0.0009,β=0.0001,r=10%的情况下来预测零件质量损失。将上述相关参数代入公式(1)中,通过数值计算得到零件平均质量损失与使用寿命关系如图1所示。
机械产品投入使用,由于各种因素影响产生质量损失,且随着服役时间增加,其平均质量损失会趋于稳定,那么这批产品几乎已经全部报废。从图1可知,这批零件的质量损失结合次数在15至20千次之间时开始大量增加,直到结合次数到30千次后,零部件的平均质量损失不再增加并稳定。所以,这批零件的寿命约在10到35千次之间。
2 产品服役寿命分布
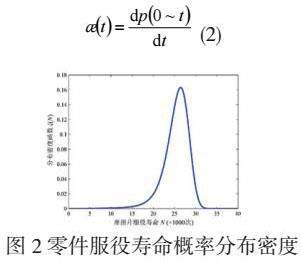
已知零件相关参数,可以通过式(2)[4]计算出其服役寿命概率分布密度函数,如图7所示。
可以看出零件服役寿命近似服从对数正态分布,这表明如果零件服役质量特征变化是一个正态分布随机过程,则基于公差要求的产品寿命分布将是一个对数正态分布。在实际生产实践中,有许多产品寿命服从对数正态分布。
从图2可以看出,产品的平均寿命约为2.5万次左右,产品的寿命几乎分布在1-3.5万次之间。此批产品的平均使用寿命可由公式(3)估算。
3 服役可靠性分析
3.1 服役可靠性分析流程
假设产品退化参量为其关键质量特征x(t)偏离目标值引起的质量损失。当产品的某关键质量特征达到其失效阈值xc时,其寿命为:
当产品质量特征为望目型时,其可靠度表达式为:
假设产品的退化参量与具有不确定性参量x的关系为:
由式(5)和式(6)可知,当获得了不确定质量特征x(t)的概率分布时,便可获得产品退化特征参量概率分布,利用概率分布可计算出产品的可靠度。
本文中对零件可靠性评价是基于几何质量特征建立的寿命分布密度函数,即公式(2),模型中的退化参量为剩余结合次数。式中,α和β为服役参数,σx(0)和μx(0)是初始关键质量特征分布参数,TL和TU是设计公差,它们都受到设计、加工和服役各种因素影响,具有一定不确定性。
3.2 服役可靠性曲线
服役寿命概率分布的概率密度函数为ζ(N),则零件结合次数为N0时失效概率为:
则结合次数为N0时的可靠度为:
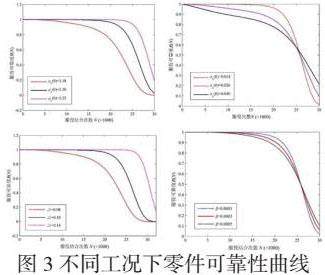
结合公式(2)和公式(8)可以得出不同设计参数、制造过程及服役工况下产品可靠性变化情况如图所示。
由可靠性曲线可以看出,产品在服役中前期时可靠度一直维持在一个较为稳定水平。当结合次数到达某一临界值时,可靠度开始急剧下降,此时产品极易发生关键质量特征超出规定范围而失效。从图3中可以看出,随着设计公差变化,生产过程稳定情况,服役系数变化等都会对产品的可靠性产生影响,这说明从设计、生产和服役角度去提高产品质量的重要性。
4 结论
本文基于相关研究基础,从产品的几何质量特征的角度出发,展开产品的服役质量损失与产品可靠性之间的关系研究,为产品的质量控制和可靠性设计提供了新的角度。结合实际测试数据分析产品的质量损失随时间的变化情况,从而得出产品寿命分布概率分布密度函数,进行其服役可靠性分析。分析得出机械产品从设计制造到投入使用的整个生命周期中各因素对产品平均使用寿命具有重要影响。此外,可通过进一步研究确定机械产品是否具备再制造价值,为机械产品的生产制造提供便捷经济的技术支持,对机械产品质量控制及提高企业效益也具有重要意义。
参考文献
Haugen E B. Probabilistic mechanical design[M]. New York: John Wiley&Sons, 1980.
Yin X Q, Mo Y D, Dong C C, et al. Identification of the influential parts in a complex mechanical product from a reliability perspective using complex network theory[J]. Quality and Reliability Engineering International, 2020, 36(2): 604-622.
Yu J W, Zheng S L, Pham H, et al. Reliability modeling of multi-state degraded repairable systems and its applications to automotive systems[J]. Quality and Reliability Engineering International, 2018, 34(3): 459-474.
Liu X T, Mao K, Wang X L, et al. A modified quality loss model of service life prediction for preducts via wear regularity[J]. Reliability Engineering and System Safety, 2020, 204, 107187.
基金项目:江苏海事职业技术学院校级课题《基于几何质量特征船舶柴油机服役可靠性研究》(项目编号:ZRKX07)。
作者信息:毛奎,男(1993.4—),汉族,籍贯:江苏淮安,硕士,助教,研究方向:质量可靠性。





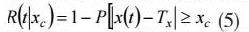
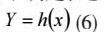
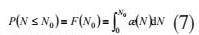
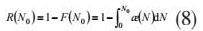
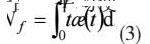
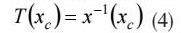

 京公网安备 11011302003690号
京公网安备 11011302003690号


