打开文本图片集

摘要：本文聚焦于初中数学中的动点问题，探讨其解题策略及相应的教学设计。通过对动点问题特点的分析，阐述了如函数法、几何分析法等多种解题策略，并结合人教版初中数学教材中的实例进行详细说明，旨在为初中数学动点问题的教学提供有益的参考。

关键词：初中数学；动点问题；解题策略；教学设计

引言：在初中数学的学习中，动点问题是一类综合性较强且具有挑战性的题型。它将代数与几何知识紧密结合，要求学生在动态变化的情境中分析问题、寻找规律并解决问题。随着教育改革的推进，对学生数学思维能力和综合运用知识能力的要求不断提高，动点问题成为了培养学生这些能力的重要载体。

一、初中数学动点问题的特点

初中数学动点问题具有三个主要特点：动态性、综合性和抽象性。其中动态性体现在点、线、图形等元素的运动变化状态，要求学生运用动态思维跟踪轨迹并分析数量关系；综合性表现为问题往往涉及几何和代数等多个知识点的综合运用；抽象性则在于点的运动过程较难理解，需要通过图形等手段将问题具体化以便分析解决。

二、初中数学动点问题的解题策略

（一）函数法

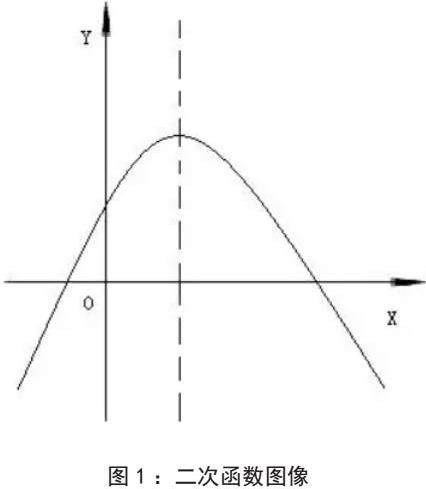
在初中数学动点问题中，函数法作为一种核心解题策略具有独特的优势。第一步是建立函数模型，需要通过合理设置动点坐标并深入挖掘几何关系来构建函数表达式。例如，当动点P（x，y）在直线上运动时，可以结合直线解析式和面积公式，巧妙地将几何问题转化为函数问题。值得注意的是，在建立函数模型时，应当充分考虑动点运动的约束条件和相关图形的特征性质。第二步是运用函数性质求解，这要求我们系统分析函数的单调性、最值和奇偶性等关键特征[1]。特别是对于二次函数y=ax²+bx+c（a≠0）这类常见情况，当a＜0时，通过求取顶点坐标不仅能准确定位动点位置，还能有效找出所求量的最大值。这种方法的优势在于能够将抽象的动态几何问题转化为具体的函数分析问题，使解题思路更加清晰。在实际应用中，函数法往往需要结合参数方程、斜率公式等多种数学工具，通过建立恰当的函数关系，系统地分析函数图像的变化规律，从而找到问题的突破口。此外，在使用函数法解决动点问题时，绘制辅助图形和构建坐标系的选择也显得尤为重要，它们能帮助我们更直观地理解问题本质，为建立正确的函数模型奠定基础。如图1：

（二）几何分析法

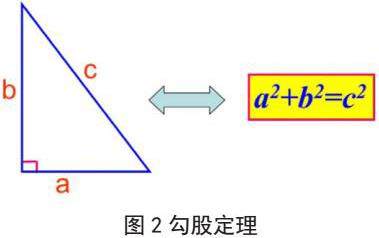
几何分析法是解决动点问题的重要方法，它通过深入分析图形的基本性质和应用几何定理来寻找解题思路。在具体应用中，首先需要充分利用三角形的全等相似性质、四边形的特征以及圆的基本性质来建立等量关系，例如在处理平行四边形上动点问题时，可以利用其对边平行且相等的性质巧妙构造相似三角形，从而推导出重要的比例关系。当问题涉及直角三角形时，勾股定理a² + b² = c²和三角函数sinA = a/c、cosA = b/c、tanA = a/b等基本公式成为关键工具，通过分析已知的边长角度关系来求解未知量。在实际解题过程中，几何分析法往往需要结合辅助线的添加和特殊点的构造，通过发现隐含的几何关系来简化问题[2]。此外，合理运用全等三角形的判定条件、相似三角形的判定条件以及各种四边形的性质，能够帮助我们更有效地分析动点在运动过程中产生的几何关系变化，从而找到问题的突破口。灵活运用几何分析法不仅能够培养学生的空间想象能力，还能提高其逻辑推理能力。如图2：

（三）分类讨论法

分类讨论法在动点问题中的应用需要两个关键步骤。首先是确定分类标准，因为动点在运动过程中可能出现在不同位置，会导致结果产生差异，比如当动点在线段上运动时，就需要考虑端点、中点和线段内部等不同情况；其次是针对每类情况进行具体分析和计算，最终得出完整答案，例如在等腰三角形的动点问题中，需要分别讨论动点在底边和腰上运动的情况，计算不同位置下的周长或面积。在运用分类讨论法时，关键是要确保分类的完整性和互斥性，避免遗漏或重复。同时，还要注意动点在不同区域运动时可能产生的特殊情况，如函数的连续性变化、图形性质的突变等。另外，在实际解题过程中，分类讨论往往需要结合函数法或几何分析法，通过建立合适的数学模型，系统分析每种情况下的数量关系和几何特征。特别是在涉及最值问题时，不同区域的最值点可能出现在区间端点或内部的特殊位置，这就需要我们通过严密的数学推导，找出所有可能的最值点并加以比较[3]。合理运用分类讨论法不仅能提高解题的准确性，还能培养学生全面思考和系统分析的能力。

三、初中数学动点问题的教学设计

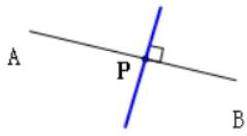
在教学动点问题时，我设计了一个典型例题——在线段AB上取一动点P，过P作AC的垂线PH（H在AC上），已知AB=4，AC=3，求PH的最大值。如图3：

课堂伊始，教师可以用动态几何软件展示点P在AB上移动时垂线PH长度的变化，引发学生思考PH长度的变化规律。接着，通过建立平面直角坐标系，将问题转化为数学模型：以A为原点，AB沿x轴正方向，AC沿y轴正方向，设P点坐标为（x，0），H点坐标为（0，y）。

在解题过程中，重点引导学生发现关键等量关系。由于PH垂直于AC，可以利用相似三角形得到x：4=y：3，从而得到y=（3x）/4。再利用PH²=x²+y²，代入得到PH²=x²+（3x/4）²。通过求导，最终可求得最大值。

为巩固学习效果，教师应组织学生分组讨论这道题的其他解法，如几何分析法。同时设计一些相关的练习题，让学生通过独立思考和合作交流来掌握动点问题的解题思路和方法。

通过这个教学过程，既培养了学生的空间想象能力和数形结合思维，又让学生体会到数学知识的内在联系，达到了预期的教学目标。在教学中，教师应特别注重通过启发式教学和探究式学习，激发学生的学习兴趣，培养其主动探究精神。

结语：初中数学动点问题的教学涉及数学思维的多个方面，对培养学生的几何直观能力、函数思维和推理能力都具有重要价值。在实际教学中，教师要注重培养学生对动点轨迹的空间想象，引导其灵活运用函数、几何和分类讨论等多种方法分析问题。同时，通过小组探究、成果展示等多样化的教学活动，不仅能激发学生的学习兴趣，还能培养其数学交流和团队协作能力。在今后的教学实践中，教师应当继续探索更有效的教学策略，帮助学生更好地理解和掌握动点问题，提升其数学核心素养。

参考文献：

[1]陈君.初中数学动点问题的解题思路[J].大东方，2024，6（15）：

[2]苏雅.深度学习视域下初中动点问题的学习现状调查研究[D].扬州大学，2024.

[3]王媛媛.初中数学中动点问题的教学实践研究[D].湖南师范大学，2018.