打开文本图片集

作者简介：姚敏强（1982—  ），男，山西临汾人，硕士，工程师，研究方向为航空发动机市场和项目管理。

通信地址：四川省成都市新都区蜀龙大道成发工业园姚敏强

摘 要：本论文在航空发动机机匣族类零件工时定额初步拟定的基础上，通过MES系统搭建和收集样本库，采用中位数排序集抽样，逆向迭代学习持续优化形成零件的工序工时定额估计方法。

Abstract： On the basis of the preliminary formulation of the working hour quota for the parts of aero engine casing， this article puts forward the method to estimate norm of parts’process working hours by building MES system， collecting sample database， applying median ranking set sampling， and reversing iterative learning for continuous optimization.

关键词：工时定额，MES系统，中位数排序集抽样（MRSS），迭代学习

Keywords： norm of working hours， MES system， median ranking set sampling， iterative learning

引言

航空发动机结构复杂，零部件数量庞大，加工工艺门类多样，生产周期长，具备典型的多品种小批量的生产组织模式。同时工时定额是企业计划管理、成本测算和运营管理的重要依据，也是优化企业管理的重要基础。为了有效提高航空发动机企业设备利用率、优化计划管理、深化成本管理、进一步提升企业的竞争力，迫切地需对航空发动机零件生产进行精细化的工时定额测算。公司当前的机匣族类产品工时定额体系机制暴露出工时定额不准确、问题工时反馈不及时、员工积极性发挥不明显等问题，考虑既有定额工时的延续性和改进的长期性，结合公司正在推进的MES管理系统进行工时样本收集和统计，通过中位数排序集抽样的方式进行持续迭代学习，逐步实现工时定额的科学性和合理性，达到优化计划管理、绩效管理、提升企业效益的目标。

1工时定额确定方法的现状

工时定额是企业计划管理、成本测算和运营管理的重要依据，也是优化企业科学管理的重要基础，其计算的准确性将影响到企业的生产、经营和管理水平。在航空发动机生产制造行业，工时定额往往是航空发动机零部件产品研发阶段初步确定，后续在批量生产阶段不断调整确定形成的。目前在航空航天行业有不少人对工时定额做了相关研究，韩宇等人[1]提出工时定额制定的方法主要有经验估工法、技术测定法、比较类推法、统计分析法。熊伟等人[2]提出随着计算机技术和先进制造技术的不断发展和应用，计算机查表法、数学模型法、神经网络法和混合法等方法相继出现，也做了基于SLFM 神经网络模型的计算工时定额的测算研究.董晓芳等人[3]构造了基于的中位数估计量， 证明了其估计量具有强相合性和渐近正态性，并讨论了相对于下中位数估计的渐近效率， 证明出中位数排序集抽样效率高于排序集抽样和简单随机抽样，这点使得统计分析法上有了更好方向。但各企业的工时定额都有自身的特点，目前公司机匣族类零件的机加工工序有超过6000个，每月完工信息量多达20000余条，同时工时样本中存在较多的极端值，前面提出的工时定额方法也有一定的局限性，在企业具体的工作中要结合自身的情况进行思考并综合运用。

2采用中位数排序集抽样的非参数估计

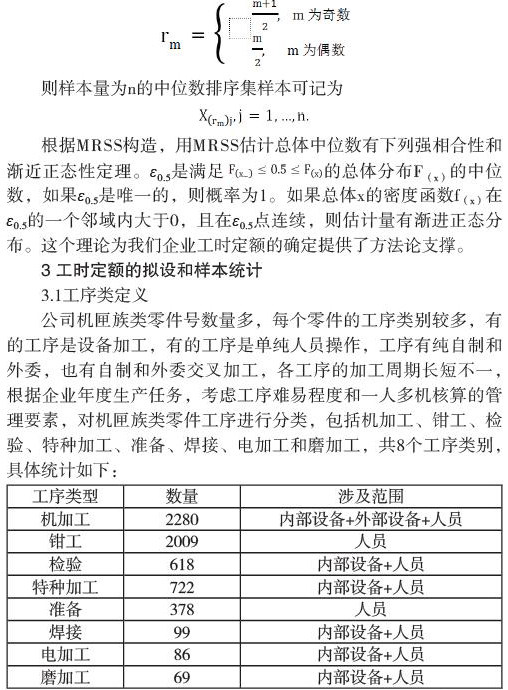
中位数排序集抽样（简称为MRSS）是排序集抽样（简称为RSS）派生出来的一种抽样方法，广泛应用于农业、环境、经济和生物科学等方面。按照董晓芳等人[3]提出的MRSS构造过程，MRSS是从总体样本中随机抽取大小为mn的样本，分为n组，每组m个，对每组分别由小到大进行排序，如果m为奇数，则从每组中抽出次序为（m+1）/2的样本单元并测量，如果m为偶数，则每组中抽出次序为m/2的样本单元并测量。如令

则样本量为n的中位数排序集样本可记为

根据MRSS构造，用MRSS估计总体中位数有下列强相合性和渐近正态性定理。ε0.5是满足的总体分布F（x）的中位数，如果ε0.5是唯一的，则概率为1。如果总体x的密度函数f（x）在ε0.5的一个邻域内大于0，且在ε0.5点连续，则估计量有渐进正态分布。这个理论为我们企业工时定额的确定提供了方法论支撑。

3 工时定额的拟设和样本统计

3.1工序类定义

公司机匣族类零件号数量多，每个零件的工序类别较多，有的工序是设备加工，有的工序是单纯人员操作，工序有纯自制和外委，也有自制和外委交叉加工，各工序的加工周期长短不一，根据企业年度生产任务，考虑工序难易程度和一人多机核算的管理要素，对机匣族类零件工序进行分类，包括机加工、钳工、检验、特种加工、准备、焊接、电加工和磨加工，共8个工序类别，具体统计如下：

如前所述，企业进行工时定额的目的是为了有效提高企业设备利用率、优化计划管理、深化成本管理、进一步提升企业的竞争力，所以在工厂的层面做工时定额的范围框定在企业成本费用占用较大的内部设备和人员上，因此我们选取机加工、钳工、焊接、电加工和磨加工工序开展工时定额细化工作。

3.2工时定额拟设

工序工时定额由单件准结工时和单件加工工时，单件准结工时等于工序准结工时除以分摊批量，工序准结时间由工序准备时间和工序结束时间组成。往往工序工时定额受设备型号、设备精度、自动化程度、工人熟练度和测量难易度影响，但是企业内部同一个工序在不同设备和不同操作人员的实做工时都存在差异。所以我们开展的工时定额细化工作要同时兼顾各类因素，从统计学和MRSS估计来看，即使考虑这些差异性，针对同一产品同一工序，用MRSS估计总体中位数得出的工时定额也具备有强相合性和渐近正态性。

工时现场绩效工时的统计逐步趋于合理的基础上，在进行MRSS估计工时定额之前，我们采用经验估工法和技术测定法对机加工、钳工、焊接、电加工和磨加工工序定额工时进行拟设。在原有标准工时的基础上，通过与基层领导人员和操作工人采用经验数据形成经验工时，同时技术人员根据加工工艺步骤通过工艺模拟软件形成仿真工时，利用标准工时、经验工时和仿真工时三个数据进行差异化分析和讨论，完成对机匣族类零件的目标工序拟设工时，这个拟设工时定义为实做工时。

3.3样本收集和过程管理

如前所述，样本收集选取机加工、钳工、焊接、电加工和磨加工工序，企业当前参与此类工序设备110余台，人员260余人，工序6000余个，每月完工约15000人次，并且同一工序存在多个设备多个人员同时参与的情况，样本收集的方式是否科学也会影响到工时定额MRSS估计。经过前期多种方式收集，通过采用员工交班本、工段长人工统计和MES系统等方式，采用员工交班本和工段长人工统计方式由于数据量巨大和人为干扰造成部分数据失真，采用MES系统统计方式，易于标准化和汇总，数据相对真实。

综上，我们确定样本收集的方式为MES系统统计。为了确保数据接近实际，我们对MES系统的统计模式和报工管理方式进行开发和管理，计划收集6个月的收集，进行MRSS估计，后期三个月为周期进行重复MRSS估计并按学习曲线进行工时定额迭代。

样本收集的有效性和准确度决定MRSS估计的可靠性，通过MES统计的关键点在于各工序开工和结束报工的及时性。在样本管理的过程中，通过建立MES报工报工管理细则规范员工的开始结束报工要求，在前期三个月开展每天MES报工随机抽查，督促员工养成及时报工的良好习惯，项目运行至今MES报工月度及时准确率达到95%，为后续MRSS估计奠定了基础。

4 采用MRSS估计进行迭代和学习曲线管理

MRSS估计进行迭代得到可靠中位数，需要考虑样本数量和迭代循环频次两个关键因素。航发发动机机匣族类产品本身特点是多品种小批量，本项目要得到可靠中位数的周期需求相对较长，考虑循环迭代持续优化，定义单次MRSS估计样本数量不低于5个，循环频次为1个季度。

本项目MRSS估计使用EXCEL软件自动公式进行，单次MRSS估计建议总样本数不超过5万个。由于存在同一工序存在多名员工报工的情况，在MRSS估计前对样本进行前置处理，把样本数据的单位调整统一，公式设置的原则具体如下

通过MRSS估计后，对总样本的估计值进行数据透视可得出样本工序的中位数，再次把中位数设置为实做工时，导入MES系统基础数据库，根据循环频次进行学习管理，样本数据越大MRSS估计中位数就越准确，后期学习管理时必须兼顾到零件工序的工艺改进和工序调整，在对样本进行前置判断和处理。

5 结论

本文针对航空发动机机匣族类产品建立了工序工时MRSS估计中位数的一般方法，给出了目标工序工时的估计规则，并应用MRSS估计模型估算工序工时算法，识别出影响样本数据的因素并给出前置处理建议。与现行的经验估工法、技术测定法、比较类推法和统计分析法对比，引入了MES信息化统计手段后MRSS估计具备准确度高、速度快，可迭代自我学习等优点，为解决航空发动机多品种小批量的产品工序工时估算思路提供了创新型的思路，为推行产品精益生产提供了准确的工时数据支撑，进一步推动提升企业的运营效益。

参考文献：

[1]韩宇 王耀 崔国星 张杰.基于多工种、多品种生产模式建立工时定额标准的探索与实践[J].航天工业管理，2019，12期

[2]熊伟 孙根正 陈冰 李山.航空发动机叶片数控加工工时估算方法研究[J].数控加工，2014，8期

[3]董晓芳 张良勇.基于中位数排序集抽样的非参数估计[J].数理统计与管理，2013第32卷第3期

[4]Ozturk O，Wolfe D A. An improved ranked set two-sample Mann-Whitney-Wilcoxon test[3].Can.J.Statist.，2000，28：123-135.

[5]吴骏 黄青云.基于数学史的平均数、中位数和众数的理解[J].数学通报，2013第52卷第11期

[5]陈义时 孙根正 王刚 陈冰 李建荣.航空发动机零件工时定额测算技术研究与实现[J].航空制造技术，2012第1/2期