打开文本图片集

摘要：近年来，我国仓储物流事业迅速发展，交通条件也越来越便利，一些参考行政区划的物资仓库布局到了要重新规划的时候。针对这一情形，本文研究仓库聚类融合问题，首先构建基于成本导向的仓库聚类融合模型，然后将K-means聚类算法和遗传算法结合起来，用来求解相关聚类问题，最后引入案例，代入模型算法求出仓库聚类融合成本最优方案，为相关企业优化仓库布局、提高运营效益提供行之有效的方法策略。

关键词：仓库聚类融合；K-means聚类算法；遗传算法

0 引言

随着经济全球化和现代信息网络技术的日益完善，世界贸易和运输的迅速发展，物流业在国民经济中的地位日益提高，已成为重要的新兴产业。物流是贯穿产品生产、流通、消费全过程的系统工程，由仓储、运输、配送、包装、装卸、流通、信息等多个环节组成，各环节有机衔接，密不可分。仓储是现代物流的重要组成部分，仓储活动及其管理直接影响物流系统的质量和效率。[1]

改革开放以来，特别是进入21世纪，我国的仓储物流事业逐渐发展，产业规模不断扩大，同时也暴露出许多问题。在一些业务范围涉及全国的大型国有企业中，物资仓库的设置通常参考政府的行政区划，每个省、每个市甚至每个县都要设置一个物资存放仓库。这一举措确保了仓储配送的准时性，但也在很大程度上浪费了许多仓储空间，无形中增加了企业的仓储物流成本。近年来，随着我国经济的发展，交通越来越便利，仓储配送的时效性也更加依赖便利的交通条件，一些参考行政区划的物资仓库布局到了要重新规划的时候，在许多大型国有企业中，关于仓库聚类融合的研究势在必行。

1 聚类融合相关理论

聚类分析是统计学所研究的“物以类聚”问题的一种方法，它属于多变量统计分析的范畴。它是一种建立分类的方法， 能够将一批样本数据按照他们在性质上的亲疏程度在没有先验知识的情况下自动进行分类。一个类就是一个具有相似性的个性的集合， 不同类之间具有明显的非相似性。[2]利用聚类，人们可识别密集和稀疏的区域，并可发现很多潜在的不容易被发现的规律，特别是一些具有相似性的类别规律。随着大数据时代数据指数级增长，聚类的研究在数据挖掘领域变得越来越活跃。[3]

聚类方法的种类有很多，而K-means算法是其中重要的一种。K-means聚类算法由Steinhaus（于1955年）、Ball&Hall（于1955年）、Loyd（于1957年）、和McQueen（于1967年）在各自不同的科研领域独立地提出，至今仍然是聚类算法乃至数据挖掘领域中的研究热口方向。 [3]但是，K-means聚类算法在解决早熟和局部最优等问题方面存在不足，而一些智能算法具有扩大搜索解范围的能力，因此出现很多智能算法与聚类算法融合的新算法。[4]比如先利用K-means聚类算法求出初始解，再运用遗传算法进行聚类分析。这种融合算法不需要事前给定最终的簇个数，可发现任意的簇，且具有搜索全局最优解功能。因此本文构建仓库聚类融合模型，先利用K-means聚类算法求出初始解，再运用遗传算法去求解仓库聚类融合问题的最优解。

2 基于成本导向的仓库聚类融合模型

2.1 场景描述

存在m个地市分屯库，要求对其进行聚类融合，聚类数量不能大于n个。参照多个维度的数据，最终将其划分为k个聚类，选取k个聚类中心库融合聚类里的其他库，使得一定时期内的总运输成本、总仓租成本以及总人工成本之和最低。

2.2 模型构建

2.4 参数说明

（1）n表示最大聚类数量； （2）k表示待决策聚类数量；

（3）m表示地市分屯库个数； （4）qi表示第i个地市分屯库的年均运输量；

（5）wi表示第i个地市分屯库的年均库存金额； （6）dij表示聚类中心库与地市分屯库间的运输距离；

（7）rj表示第j个聚类中心库单位面积的租赁单价； （8）

（9） （10）sj表示第j个聚类中心库所管理物资需要的人工数量；

（11）c表示吨公里运费； （12）t表示万元金额物资需要的租赁面积；

（13）f表示该地区单位人工的年平均成本；

3 基于遗传算法的K-means仓库聚类求解

3.1 遗传算法

遗传算法（Genetic Algorithm）在 1975 年被 J.Holland 教授首次提出，它是借由模拟自然进化过程来找最优解，详细来说，它主要模拟生物进化论中的自然选择（适者生存，优胜劣汰）和遗传学中的生物进化过程中的计算模型，通过启发式算法求解最优值，在这个过程中，采用简单的编码来反映各种复杂多变的自然选择的过程，并得到最终搜索目标，形成一种求解最优值的启发式算法。因此它能够解决许多常规方法尚无法处理的复杂问题的优化。[5]

3.2 K-means算法

K-means算法是一种数据统计分类和聚类的方法，它的基本思想是通过计算样本之间的相似度或欧式距离来将数据分为K个类别。同一聚类中的对象相似度较高，而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”来进行计算的。[3]

3.3 基于遗传算法的K-means仓库聚类求解步骤

第一步：数据输入和参数设置

输入某企业在某省份单位库存所需仓储面积、年平均工资以及该省份的单位运费等数据；输入需要进行聚类融合的各地市分屯库的地理坐标、年均库存量、用工数量、单位仓租以及各地市分屯库之间的运输距离等数据；设置遗传算法的初始种群规模、迭代进化次数、自然选择概率、交叉进化概率以及变异进化概率等参数。

第二步：K-means算法——求得问题的一组初始解

K-means算法的具体步骤是：首先，随机选择k个数据点作为初始聚类中心。其次，对每个数据点，都计算其到全部k个聚类中心的距离，然后将该数据点分配给距离最近的那个聚类中心所代表的聚类。下一步，针对每个聚类重新计算聚类中的所有点的平均值，作为新的聚类中心。最后，重复以上两步，直到聚类中心不再发生变化或者是经过了预定的迭代次数。本文平均加权经度、纬度、年均库存金额等多个维度进行聚类，在MATLAB 2023a上重复运行软件自带的kmeans函数，求得仓库聚类融合问题的一组初始解。

第三步：遗传算法——确定适应度函数

将仓库聚类融合模型中的目标函数转化为便于遗传算法运行的适应度函数，遗传算法会将进化迭代后的解集代入适应度函数，再根据适应度函数的大小确定下一步的进化迭代方向。

第四步：遗传算法——自然选择

基于kmeans函数求出的初始解集，执行遗传算法的自然选择操作。自然选择是遗传算法的关键，毕竟我们需要的就是最优解，不对种群进行选择肯定得不到最优解的。自然选择时，适应度越大的解越容易被选择。

第五步：遗传算法——交叉进化

基于自然选择后的解集，执行遗传算法的交叉进化操作。如果一堆初始解中没有最优解，则需要在选择过程中让解也在变化。形象地理解就是，一直选择就相当于无性繁殖，克隆，没有什么变化；而交叉则是有性生殖，就是“龙生九子，十子不同”，这样能够保证解的多样性，有可能出现最适的解并在选择当中得以保存下来。并且，交叉这个步骤是可以保留父母双方的优良性状的，之后保留下来的优良性状又会继续交叉从而传递给下一代。

第六步：遗传算法——变异进化

基于交叉进化后的解集，再执行遗传算法的变异进化操作。变异进化与交叉进化的目的相同，都是为了产生初始解集之外的更优解。在初始解集进化程度较低时，变异进化可以使得种群快速摆脱初始解集，更快地寻找到问题的最优解。

第七步：遗传算法——迭代后输出问题的最优解

将每次变异进化后的解集作为新的初始解集，重复进行选择——交叉——变异的操作。根据事先设置好的迭代次数终止遗传算法，通过比较每次迭代后的局部最优解，输出全局最优解。

4 案例引入——移动公司C在H省的物资仓库聚类融合

4.1 案例介绍

移动公司C在H省的每一个地市都设置有一个物资仓库，来为本地市的分公司提供通信物资供应。应上级部门“降本增效”相关文件的要求，C公司计划对H省内各地市的物资仓库进行聚类融合，以节约仓储成本，提高H省配送系统的整体运作效益。如图1所示。

4.2 数据引入

已知信息有：

（1）H省各地市分屯库的地理坐标，H省各地市分屯库每年每平米的仓租价格、所需的人工数量，以及近几年H省各地市分屯库的年均运输量、年均库存金额，如表1所示；

（2）H省各地市分屯库之间的运输距离，如表2-1、表2-2所示；

（3）C公司万元金额物资需要的租赁面积为0.2平方米，H省境内吨公里运费为0.3元，C公司员工在H省的平均年薪约为70000元。

4.3 案例求解

（1）K-means算法初步求解

首先基于以上数据构建模型，在MATLAB 2023a上直接调用K-means算法，将K值设置为6，输入经度、纬度、年均库存金额等多个维度的数据，多次重复运行K-means算法，得出聚类融合方案的一个初始解集，在初始解集中选择一个K-means算法下成本最优的聚类融合方案，如图2所示。

图2中，一种颜色代表一种聚类，正方形图标代表聚类中心库，最低聚类成本的单位是元。从图2可以看出，考虑3个维度数据的K-means算法求得的结果并不是很理想，成本应当还有压降的空间。因此，需要在K-means算法求得的初始解集的基础上，运行遗传算法，求得成本更优的聚类融合方案。

图2 K-means算法下聚类融合成本最优方案

（2）遗传算法求聚类融合成本最优方案

将K-means算法求出的初始解集作为初始种群，在MATLAB 2023a上运行遗传算法，限定最大聚类数量为6，将遗传算法的选择程序概率设置为0.8，交叉程序概率设置为0.9，变异程序概率设置为0.05，迭代次数设置为5000次。多次重复运行遗传算法，可以得出聚类融合成本最优方案，如图3-图4所示。由图4可以看出，6聚类中心方案中产生了聚类融合成本最优方案：

聚类1：库5；

聚类2：库12；

聚类3：库3、库4，聚类中心库为库4；

聚类4：库13、库14、库17，聚类中心库为库14；

聚类5：库8、库10、库11、库16，聚类中心库为库10；

聚类6：库1、库2、库6、库7、库9、库15，聚类中心库为库1；

最低聚类融合成本：约为11286175元。

（3）遗传算法求得的其他成本较优的聚类融合方案

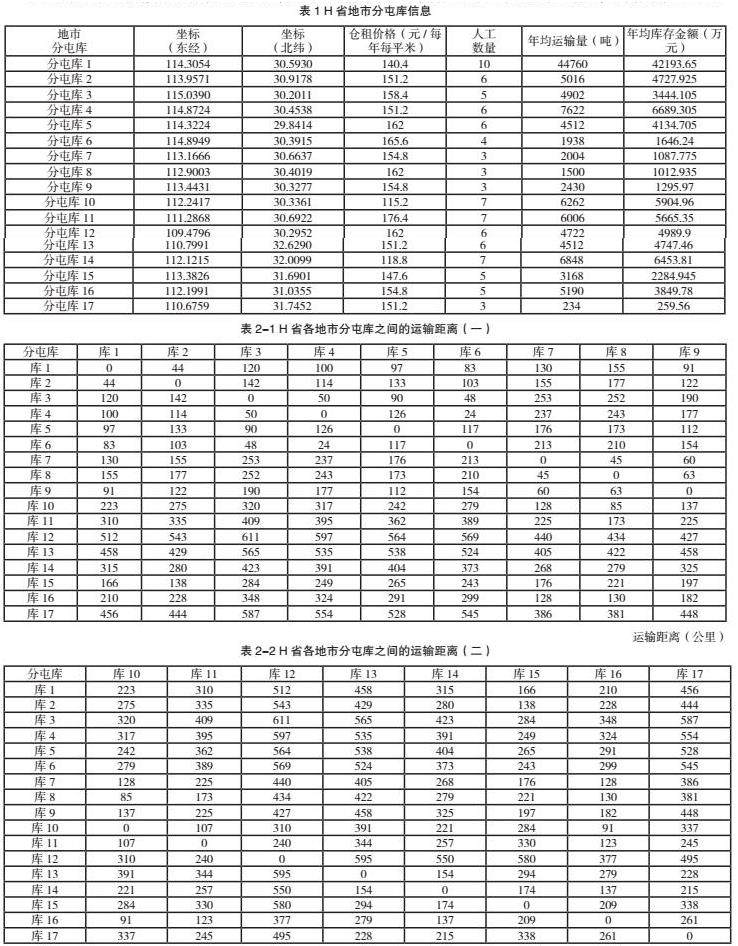
为了给C公司在H省的物资仓库聚类融合计划提供更多的支持，给出遗传算法求得的4聚类中心成本最优方案和5聚类中心成本最优方案，如图5-图6所示。

5 总结

针对K-means聚类算法需要事前给定最终的簇个数，一些时候难以求得问题的全局最优解的弊端，本文结合运用K-means聚类算法和遗传算法来求解物资仓库聚类融合问题。通过案例表明，结合运用K-means聚类算法和智能算法求得的聚类结果要比单独运用K-means聚类算法求得的聚类结果有着更好的经济效益。本文为相关企业实施物资仓库聚类融合计划提供了一种经济效益更高的解决方案。

参考文献：

[1]刘庭翠，沈捷.仓储与配送实务[M].重庆：重庆大学出版社，2022.

[2]祝丽，汝宜红，罗平.基于聚类分析电信运营企业仓库布局优化研究[J].物流技术，2007， （08）：106-109.

[3]左倪娜.基于现代优化算法的K-means聚类的研究与应用[D].广西大学，2016.

[4]李振.K-Means算法研究及其与智能算法的融合[D].安徽大学，2016.

[5]田延硕.遗传算法的研究与应用[D].电子科技大学，2004.

作者简介：史继祥（1992.12—），男，汉族，江苏连云港，大学本科，主要从事工作：供应链管理，通信管理

马维（1997.10—），男，汉族，山西大同，硕士，主要从事工作：物流管理，供应链管理

刘沁荣（1998.10—），女，汉族，山西朔州，大学本科，主要从事工作：物流管理，采购与供应链管理