打开文本图片集

摘 要：依据课程改革的需要和教育观念的深入，广大教师越来越重视数学思维品质的培养。小学阶段学生能够养成一个良好的思维习惯，善于思考，这会给以后的学习打下扎实的基础。良好思维的培养是数学教育的本质，而教师也应准确把握这一教育目的，转变自身的教学行为。本文基于小学生灵活数学思维品质的培养，对教学行为的转变进行分析。

关键词：数学;思维品质;灵活性;教学行为

以往的数学课堂，教师比较注重教学的效率。这种快节奏、讲求实效性的教学观念对小学生的内心需要置若罔闻，从而导致学生的思维得不到训练，带给学生的危害显而易见，比如小学生独立思考能力差，知识迁移存在困难，无法灵活应用数学知识等。因此，在小学数学教学中，要不断改进教学行为，以此培养学生灵活的思维品质，提高学生的思维能力，促进学生更好地掌握知识，提高教学质量。

一、数学思维品质、教学行为的界说

（一）数学思维品质

数学思维品质又称为数学思维的智力品质，即思维的深刻性、广阔性、灵活性、批判性、创造性等等，它起着衡量数学思维发展水平的作用。在实际教学中，经常可以发现有的学生反应快，灵活;而有的学生反应慢，呆板，这就是思维品质的差异。在数学教学中，思维的灵活性是指能依据客观条件的变化及时调整思维的方向，全面地、科学地考察问题、分析问题，及时地提出新的设想和解题方案，不受思维定势和模式的束缚。不仅能够把握住事物的全体，抓住事物的基本特征，而且也不会忽视重要的细节问题。

（二）教学行为

广义的教学行为是指一切与教学有关的教育活动。狭义的教学行为是指课堂教学中，教师采取的外显的、可观察的行为。也就是，教师的教学行为是指教师在课堂教学中影响学生学习的一切活动或表现。由此，我们把教师的课堂教学行为定义为教师在课堂特定的情景下，以学生发展和自身发展为整体目标，周而复始连续性的从事各种活动。

二、改进数学课堂教学行为的若干案例

在实际教学中，教师往往重视集中思维的训练，或者采用讲授的教学方式，凡此种种，均不能起到良好的教学效果。发散思维是学会学习的关键思维品质，是进行知识迁移不可或缺的，也是适应未来生活必备的。以提高小学生思维的灵活性为目标，兼顾培养发散思维，我在教学实践中做了一些探索与思考。

（一）教学方式：从“教师的教”转为“学生的学”

小学数学教学中，图形与几何这部分知识一直都是重难点，尤其是图形公式的推导。实际课堂上，教师对于图形公式的讲解并不透彻，学生对于新知识的学习是一知半解，大多数时候死记硬背公式。因此，转变课堂上的教学方式刻不容缓，从“教师主导的教”转为“学生主导的学”，下面以某一课例进行分析。

[案例描述]人教版五年级上册《平行四边形的面积》这一课的公式推导，教材的例题出示了含有一个平行四边形和一个长方形的格子图，常规课堂中，在教师的引导下，学生先数出方格数然后完成表格（一个方格代表1 m²，不满一格的都按半格计算），接着，教师会直接提问：同学们观察表格里的数据，你发现了什么？学生对于这个问题的答案保持惊人的一致：通过数方格我们发现，平行四边形的底和长方形的长相等，平行四边形的高和长方形的宽相等，平行四边形的面积和长方形的面积也相等，猜想：平行四边形的面积=底×高。

[问题探讨]数格子的方法，得出图形各部分的数据，能有力证明图形的面积与各部分的关系;类比长方形的面积计算公式，得出平行四边形面积公式的猜想，在小学阶段是常用的方法，也适合现阶段学生的思维方式。看似完美无缺，但从实际教学效果来看并不让人满意，认真反思可能存在以下两点原因：

其一：由于教师习惯性地主导课堂，让学生跟着已经设定好的思路走，导致学生的猜想只有一种，限制了他们的思维，不利于灵活性思维品质的培养。在错误例子中可以反映出来，很多学生解决问题时运用了“平行四边形面积=邻边×邻边”这一错误公式，并没有选择正确的面积公式，说明学生没有掌握公式的推导过程，不是真正理解公式的含义。

其二：用一组数据得出猜想，不够严谨。数学中不完全归纳法，至少需要三组数据的支撑，才能基本符合得出某一结论的要求，然而，本例题中只有一组数据，着实不够严谨。这一弊端，不利于学生细致严谨态度的养成，也会造成学生对科学方法的误解。

[教学改进]针对案例中存在的问题，教师应合理利用新旧知识之间的联系，放手让学生进行大胆的猜想，既是为了激发学生的学习兴趣，也是为了探索平行四边形的面积打下基础。

师：老师这里有个平行四边形，你们认为这个平行四边形的面积怎么列式呢？请大胆猜一猜？（课件出示）

生1：我认为，平行四边形的面积=7×5。因为长方形的面积=长×宽，所以我猜想平行四边形的面积是用两个邻边的长度相乘。

生2：我有不同意见，平行四边形的面积=7×4。因为平行四边形和长方形之间是有联系的，可以把平行四边形转化成我们熟悉的长方形，利用转化后的长方形的面积就能求出平行四边形的面积，所以我猜想平行四边形的面积=底×高。

改进后的课例是直接出示一个平行四边形，给出两条邻边和其中一条高，让学生自由猜想平行四边的面积计算公式，那么猜想是多样的，更有利于培养学生的创新意识和灵活的思维品质。

（二）问题设计：从“封闭式问题”转为“开放式问题”

数学从问题出发，问题是数学学科的“核心”，一代又一代的数学家提出数学问题，孜孜不倦地对问题进行研究探索，以此来推动数学这门学科不断地向前发展。由此可知，在小学数学课堂教学中，问题的设计非常关键，不同的知识内容，可以有不同的问题形式。灵活多变的题型和出题方式，对于培养学生数学思维品质的灵活性也大有裨益。下面以几种“开放式问题”设计的教学实例进行阐述。

1.结论开放式问题设计。结论开放式问题是开放性题目的一种，指题目中给出了所有已知条件，问题也非常明确，但问题的答案不唯一或者没有现成的结论。解决这类问题时，引导学生尽可能多地探究寻找相关结论，多维度、多角度来思考，不仅需要思考条件本身，而且要思考条件之间的关系，综合运用与变换手段来处理数学信息，得出结论，有利于坚忍不拔的钻研精神和创新精神的培养，也有助于灵活数学思维品质的培养。

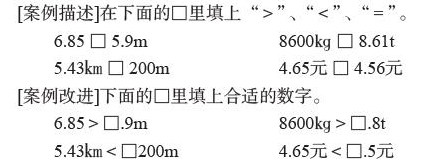
[案例描述]在下面的□里填上“>”、“<”、“=”。

6.85 □ 5.9m 8600㎏ □ 8.61t

5.43㎞ □ 200m 4.65元 □ 4.56元

[案例改进]下面的□里填上合适的数字。

6.85>□.9m 8600㎏>□.8t

5.43㎞<□200m 4.65元<□.5元

2.条件开放式问题设计。条件开放式问题是指题目的已知条件没有全部确定，让学生根据部分已知条件和数学问题补全数学信息的一类题型。这样设计的目的在于，引起学生对题目条件的发散思考，尽可能从不同角度来提问，进而形成“独立思考，自问自答”的良好学习习惯。教学中，教师还应及时追问，去掉或者增加某个条件，会得出什么结论呢？ 让这样的训练常态化，既能调动学生的积极性，养成善于思考的习惯，进而激发学习数学的兴趣，又能开发学生的思维，提高思维迁移的灵活性。

[案例描述]传统的题目是“封闭式问题”，包括一个或多个已知条件，需要解决一个或多个数学问题。即题目中的已知条件是确定的，无法更改，考查学生对于某一知识点的掌握情况。例如：六年级上册百分数的两道题目。

a.林场去年植树600棵，今年植树的棵数是去年的20%，今年植树多少棵？

b.林场去年植树600棵，去年植树的棵数是今年的20%，今年植树多少棵？

[案例改进]这两题是同一类型的题目，考查的内容也是一样的，只是其中一个已知条件发生了变化，出题时可以考虑合并为一道题，也可以选用其他已知条件。

例如：根据在横线上补充不同的条件，写出正确的算式。

林场去年植树600棵， ，今年植树多少棵？

（1）今年植树的棵数是去年的20%。

（2）去年植树的棵数是今年的20%。

（3）今年比去年多植树20%。

（4）去年比今年多植树20%。

总而言之，小学数学本身涉及的内容较多，教师必须要全面地对课堂教学行为进行分析、研究，以期改进教学方式，提高教学质量。以问题设计为切入点优化课堂教学方案，根据实际课堂的生成与反馈情况，充分利用情景教学、小组合作等方法深入开展小学数学教学。让学生在自主探究中，激发学习兴趣，更好地培养小学生灵活的数学思维品质。

参考文献

[1]刘明辉.谈数学思维品质灵活性与批判性的培养[J].南昌教育学院学报，2012，（6）：140.

[2]孙国芹.如何培养学生数学思维的灵活性品质[J].教学方法，2016，（15）：63.

[3]张鉴涛.小学数学高效教学行为初探[J].学校教研，2019，（3）：117.

[4]曹一鸣、王振平.基于学生数学关键能力发展的教学改进研究[J].课程与教学，2018，（3）：61.