
- 收藏
- 加入书签
基于改进蛙跳算法的含分布式电源的配电网重构方法
摘要:配电网重构是一个复杂的非线性组合优化问题。为了克服配电网重构算法存在收敛速度慢,容易陷入局部最优等问题,本文提出了一种基于分子动力学理论和云模拟理论的改进混合蛙跳配电网重构算法。在配电网的重构优化过程中,本文首先基于独立环路的整数编码策略,输入配电网初始数据,随机生成相应规模的初始种群,并判断其有效性。再基于重构网络简化法则对配电网进行简化处理,得到有效解。然后采用前推回代算法对有效解进行潮流计算。最后基于该改进的蛙跳算法对种群进行迭代优化。研究结果表明,配电网重构后,系统的有功网损显著降低。对于解决配电网重构问题,该算法不仅具有良好的寻优性能,而且收敛快,效率高。
关键词:分布式电源;配电网;重构算法;改进蛙跳算法
1 引言
智能电网中大量的分布式电源(Distributed Generator,DG)的接入对配电网的正常运行产生不可忽视的影响,对配电网电能质量、供电可靠性都带来挑战。传统的配电网重构主要改变配电网线路开关的开合状态,从而改变网络拓扑结构,达到平衡负荷、降低网损的目的。而当风电、太阳能电站等分布式电源接入配电网后,潮流的大小和方向发生改变,使得含有DG的电网重构变得复杂。
本文提出一种基于改进混合蛙跳算法的配电网重构算法。该算法借鉴分子动力学模拟[1-2]的思想,并利用云模型[3]云滴的稳定倾向性和随机性特点,采用一种新的更新策略对最差个体进行更新,从而有效地平衡了种群的多样性和搜索的高效性。
2 改进的配电网重构算法
2.1 配电网重构模型
配电网重构时一般将网损最小作为优化目标函数:
式中为系统有功损耗,为支路总数,和分别为流过支路的有功和无功功率,为支路末端的节点电压,为支路的电阻,为开关的状态变量,0表示断开,1表示闭合。配电网重构满足以下约束条件:
(1)拓扑约束,即网络中不存在孤岛和环网。
(3)支路容量约束,即实际功率不超过允许容量。
(4)潮流约束,配电网重构需满足潮流约束方程。
2.2 含分布式电源(DG)的配电网潮流计算
不同类型的DG接入配电网接口形式不同,如:太阳能光伏发电和燃料电池通过电流逆变器接入,风力发电通过异步发电机接入,地热能发电通过同步发电机接入等。不同形式的DG接口在潮流计算时使用不同的模型,如异步发电机可以简化成PQ节点,在潮流计算时应视为方向相反、功率大小相等的负荷。
式中、是节点的有功、无功功率。
光伏电池等通过电流逆变器接入电网的电源,可以看作电流和注入功率保持恒定的PI节点,相应的无功功率可以根据上依次迭代得到的电压、电流复制和有功功率计算得到,通过下式转换成PQ节点。
对于只有一个平衡节点(电源节点)的和若干个 PQ节点(负荷节点)的辐射状配电网潮流计算,前推回代法是一个编程简单、计算高效的方法[4]。
配网重构的工作流程如下:
1)输入配电系统初始数据,包括电源基准电压,节点及支路编号,各节点负荷值,开关所属环路编号;设定相应算法参数。
2)按照2.1节中的编码方法确定环路数及环路中开关对应的编号,并随机生成相应规模的初始种群。
3)判断初始解的有效性。本文采用两种判据[17]进行判断:
① 支路数=节点数-1;
② 配电网络中不存在电力“孤岛”,即按判据(1)断开相应数量的开关后,网络中各负荷节点都和电源节点连通。
4)根据2.2节对配电网进行重构简化处理,得到有效解。根据2.3节所述前推回代算法对有效解进行潮流计算,得出目标函数(网损)适应值。
5)依据2.4节所述改进蛙跳算法对初始种群进行更新优化操作。
6)判断是否收敛到全局最优解,依据为迭代次数是否到达设定进化代数。若是,则输出结果,否则重新生成种群再次进化。
3 实验与仿真
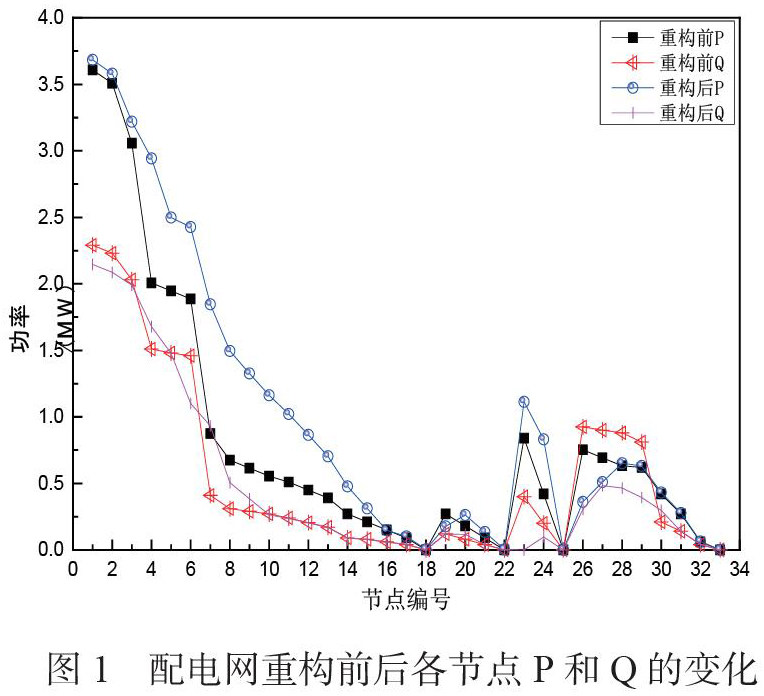
为验证本文方法的有效性,选取如图1所示IEEE33节点配网测试系统进行仿真计算。系统额定电压为12.66kV,包含33个节点,37条支路,其中联络开关5个,网络总负荷为3607kW+j2300kvar。设置种群数量为200,子群体规模为20,子群体数为10,局部深度搜索迭代次数10,全局混合迭代次数为30,比例系数为4,个体编码长度为5。仿真实验共接入4个DG,DG接入较重负荷附近,每个DG的容量小于接入点负荷。
图2显示了基于改进蛙跳算法的配电网重构方法重构前和重构后各节点有功功率P和无功功率Q的变化。从图1中看出,配电网重构后的有功功率随节点的变化规律基本一致,但总体有功功率P略高于重构之前,在4个DG接入位置附近,P值明显增高,特别在节点8接入DG时,其P值可由0.6750MW增加至1.4955MW,增幅达121.55%,而IEEE33节点配网测试系统的总P值由重构前的26.0487MW增至33.2588MW。另外,重构后各节点的无功功率Q值较重构之前更加均衡。
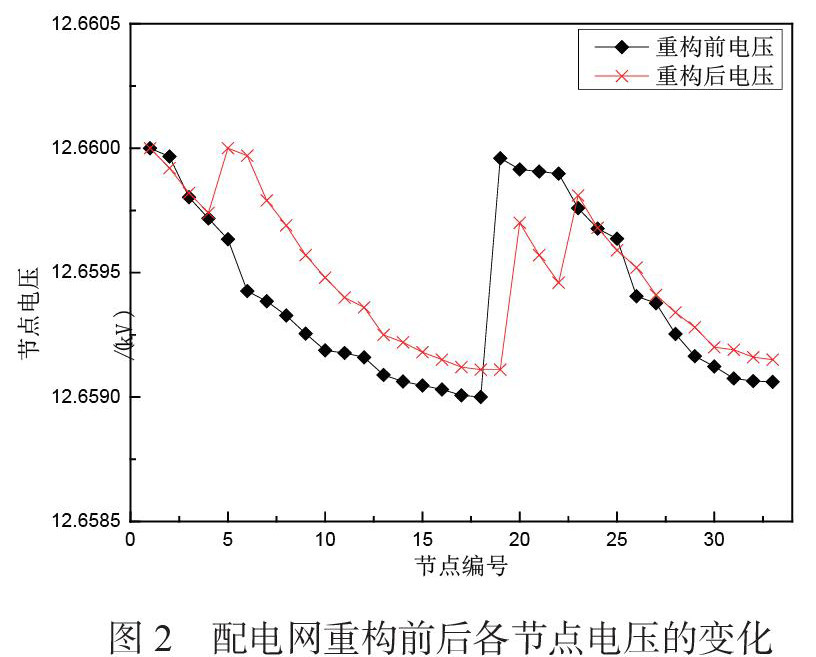
基于改进蛙跳算法对IEEE33节点配网测试系统的重构仿真,其配电网重构前后各节点的电压变化如图2所示。从图2中可以看出,在6、8、21、24节点DG接入位置,其节点电压明显增高。IEEE33节点配网测试系统各节点的电压极差值由重构前的1V降至0.85V,系统电压更加稳定。
4 结论
针对传统基于优化算法的配网重构算法收敛慢,容易陷入局部最优解的问题,本文提出一种基于改进混合蛙跳算法的配电网重构算法。该算法借鉴分子动力学模拟的思想,并利用云模型云滴的稳定倾向性和随机性特点,采用一种新的更新策略对最差个体进行更新,从而有效平衡种群的多样性和搜索的高效性。本文基于该配电网重构算法对IEEE33节点配网测试系统进行仿真计算。研究结果表明,该算法克服局部最优性能佳,全局搜索能力强,收敛速度快,能有效解决目前常用算法存在的收敛速度慢、容易陷入局部最优等问题。
参考文献
[1]Goh W F, Yoon T L, Khan S A. Molecular dynamics simulation of thermodynamic and thermal transport properties of strontium titanate with improved potential parameters. Computational Materials Science, 2012; 60: 123-129.
[2]Yang X-Q, Zhai P-C, Liu L-S, Zhang Q-J. Molecular dynamics simulation on mechanical properties of crystalline CoSb 3 with vacancy defect. Physica B: Condensed Matter, 2012; 407(12): 2234-2238.
[3]Ardagna D, Casolari S, Colajanni M, Panicucci B. Dual time-scale distributed capacity allocation and load redirect algorithms for cloud systems. Journal of Parallel and Distributed Computing, 2012; 72(6): 796-808.
[4]余昆, 曹一家, 陈星莺, 郭创新, 郑华. 含分布式电源的地区电网动态概率潮流计算. 中国电机工程学报, 2011; 31(1): 20-25.






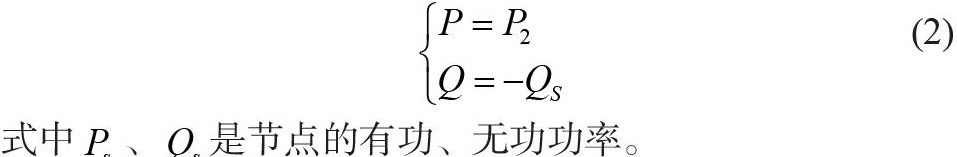
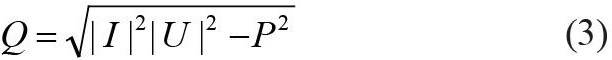

 京公网安备 11011302003690号
京公网安备 11011302003690号


