打开文本图片集

摘要：四旋翼无人机是一种具有较高载荷性能的旋翼无人机，它具有两套对称的螺旋桨，通过调整螺旋桨的旋转速度，可以改变飞机的姿态和轨道。小型四旋翼无人机因其精确悬停、垂直起降、机械结构简单等优点，尤其适用于复杂的地形和狭窄的空间；同时，四旋翼无人机在体积、结构、操作控制等方面都有着巨大的优越性，因此受到了许多控制研究机构的关注。

关键词：反步法；小型四旋翼无人飞行器；飞行控制系统

一 四旋翼分析机概述

（一）四旋翼飞机机身构造

四旋翼飞机是一种飞行系统，它的四个末端都有螺旋桨。飞机在十字架上是对称的，每一个螺旋桨都有一个马达，它可以通过调整马达的速度来调整螺旋桨的旋转速度，调整螺旋桨的升力，从而达到控制飞机的目的。

（二）四旋翼飞机飞行理论研究

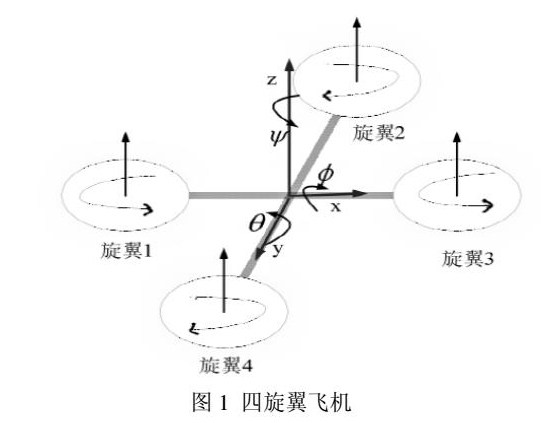
四旋翼飞机是一种欠传动的系统，它有四个输入，六个状态。四旋翼飞机是刚性体，它的空间位置和姿态可以通过在坐标轴上的旋转和围绕坐标轴的旋转来描述，而角度和直线运动是有限制的。四旋翼飞机在飞行中，各转子在产生升力的同时，也会产生与轴向相反的反向力矩，从而达到较好的偏转。

四旋翼飞机的两组螺旋桨1、3、2、4，分别是逆时针和顺时针旋转，通过四个螺旋桨的旋转速度来调整飞机的升力。它的飞行方式是这样的：

垂直起降和悬停，飞机的两套螺旋桨同时增大（降低）旋转速度，可以增大（降低）作用在机身上的升力，由此导致四旋翼飞机在竖直方向上升高或降低；四旋翼在两组螺旋桨的升力相加等于机身本身的重量时，就会使其悬停。

俯仰和前后移动，维持旋翼2，4的旋转速度，在降低（增大）旋翼3的旋转速度的同时，增大（降低）旋翼1的旋转速度，由此改变四旋翼的旋转力矩，由此在轴方向上形成升力的成分，能够实现四旋翼的纵摇和前后移动。

二 四旋翼微型无人机的反步飞行控制系统的设计

四旋翼飞机控制系统的欠驱动主要体现在四个控制量和六个自由度，其数学模型具有强耦合、强非线性、多变量等特点。在满足欠驱动特性的情况下，一般都是采用线性二次型、滑模控制、智能控制和反步法等非线性设计。在此基础上，逆步法被广泛地用于控制领域，它可以缩短调节时间、减少超调量和良好的跟踪性能，同时也可以把高阶系统分解成几个较低的子系统，同时结合 Lyapunov的稳定性，从而使控制器的结构更加明确。所以，采用逆步法进行四旋翼的控制，可以更好地满足低传动特性。另外，反步法还可以与其它控制方法一起进行系统的设计，其结果也会更好。

（一）反步法的基本原理

近年来，在求解非线性系统的控制器时，多采用逆步法，把高阶系统分为几个较低阶的子系统，并从其微分方程出发，将其引入到虚控制的理论中，从而得到所需的控制规律。在控制器的推导中，将此方法与 Lyapunov的稳定性证明结合起来，使所设计的控制器结构更加明确。

（二）RBF神经网络结构

RBF是一种前馈网络，它的最基础形式有三个层次，第一个层次是输入层，它包含一个信号源节点，它连接了网络和外部世界，将输入信号传递给隐藏层的节点；第二层次是隐藏层，该层的结点数目依赖于目标的复杂性；第三级为输出层，其输出神经元具有线性特性，其主要功能是对输入层的输入方式进行响应。RBF网络的基本思路是：隐含层节点基函数--一般选择 RBF基函数，以实现从输入空间到隐含空间的非线性转换；从隐含层到输出层的映射是一种可调整参数的线性转换，在此空间内，输出层可以对隐藏层的输出进行线性加权，从而导出权重并调整。此设计思路对改进 RBFNN的学习具有重要意义，而且能有效地解决局部最小问题，能有效地解决系统的实时性和复杂性，使其具有较强的鲁棒性和适应性。然而，在求解复杂问题时，由于 RBFNN中神经元的输入空间面积很小，因此要进行大量的隐含层节点才能达到更好的逼近效果，从而导致了学习的复杂性和学习效率的降低。

建立了一种包括复杂干扰在内的飞机数学模型；其次，采用反步方法对飞机进行位置控制，得到了飞机的升力和姿态回路的给定角度；最后，采用反向步法对姿态角和角速度环进行了设计，利用 RBF神经网络对复杂干扰进行了估算与补偿，实现了飞机对复杂干扰的抑制，提高了飞机的稳定性和飞行性能。

结束语

四旋翼飞机在飞行过程中所受的动力学和外界环境的变化，会对飞行器的一些参数产生一定的影响，比如旋转时的抖动和自身的重量会改变飞机的惯性矩，从而对飞机产生不确定的影响；同时，由于近地效应、桨叶摆动、风速变化等因素的存在，也会产生不确定的影响。

参考文献：

[1]王晓惠，谢文丹.基于5G网络的无人驾驶飞行器控制系统设计[J].长江信息通信，2022，35（02）：73-75.

[2]申遂愿，徐锦法.无人飞行器自抗扰控制研究进展[J].中南大学学报（自然科学版），2021，52（04）：1197-1212.

[3]姜鸿儒，徐利，邱令存，李迪，董诗音.基于扩张状态观测器的反馈线性化无人飞行器姿态控制[J].计算机测量与控制，2021，29（04）：95-99+125.DOI：10.16526/j.cnki.11-4762/tp.2021.04.019.

[4]黄旭，柳嘉润，贾晨辉，王昭磊，张隽.深度确定性策略梯度算法用于无人飞行器控制[J].航空学报，2021，42（11）：404-414.