打开文本图片集

摘  要：电力电缆载流量的计算对电缆线路的设计、敷设以及运行都具有重意义。因而以排管敷设电缆群为研究 对象，利用人工智能算法求解，建立了排管敷设电缆群载流量优化数值计算模型；将目标函数设定为电缆群的总载流量达到最大。在建立电缆群温度场及载流量数值计算模型的过程中，需要大量的计算模型参数，例如电缆结构尺寸参数、环境温度值及电流值等，这些参数都可用变量参数来表示，只要改变这些变量参数的赋值（如电流值），就能得到不同的计算结果（如电缆线芯温度）。变量参数取不同的值，就构成不同的设计方案，而Matlab优化设计技术就是在满足设计要求的前提下搜索最优设计方案。改进的人工智能算法的结果显示，通过设计电缆群电流分布的最优化通流方案，能最大限度地提高电缆群的总载流能力，为节能减排提供了良好的理论基础。

关  键  词：电缆；敷设方式；人工智能算法

随着科学技术的发展，现如今的电力架设形式不仅仅局限于架空线路，城市中心更是逐渐走向电缆化建设。由此，传统的电缆敷设方式虽然能够满足现如今的城市供电需求[1-3]，但缺因为敷设方式不科学，材料浪费等众多因素，限制了电力行里的发展与效率的提高。未来电力行业发展的必然选择是节能减排，建设环境友好型电力设施[4-5]。而电力电缆的载流量计算的研究更是尤为重要[6-7]。

文献[8]提出了一种考虑电力导线在自然环境如海拔高度、太阳折射温度等众多因素下输电导线的允许载流量计算方法，该方法对电网导线选型，负具有借鉴意义。文献[9]提出了一种利用传热学基本原理，根据电缆的结构参数和周围敷设区域的物性参数分析了电缆沟中电缆区域温度场分布情况，计算电缆载流量的方法。为使电缆线路高效率运行，达到节能减排的目的，因此计算载流量的方法也较多如有限差方法、边界元法和有限元法等。而电缆群载流量问题又可以看成是一个带有约束问题的目标优化问题，而智能算法是解决目标优化问题的有效方法[10-12]。

目前，智能算法[9]已经在多个领域得到推广应用。而将智能算法应用于解决控制分配问题，与传统的解法相比，它能够在受限条件下，具有更高的效率，取得更好的结果。随着技术的发展，传统的优化方法难以有效地解决在实际工程中遇到的问题，为了取得更好的优化速度和寻优结果，不少专家学者在人工智能优化方法上开辟了新的道路[13-14]。

本文是通过建立了排管敷设电缆群载流量优化数值计算模型；将目标函数设定为电缆群的总载流量达到最大。利用改进了传统的灰狼算法的种群更新方式和收敛因子的收敛方式[15，16]，以此来加快智能算法的收敛速度，和增强算法的开发和探索能力，并将其在仿真软件上进行仿真验证。

1  1问题描述

在建立电缆群温度场及载流量数值计算模型的过程中，需要大量的计算模型参数，例如电缆结构尺寸参数、环境温度值及电流值等，这些参数都可用变量参数来表示，只要改变这些变量参数的赋值（如电流值），就能得到不同的计算结果（如电缆线芯温度）。变量参数取不同的值，就构成不同的设计方案。本文是利用Matlab的强大计算功能进行仿真计算。

1.1  智能算法基本要素

在本文中，所有的仿真验证都将采用Matlab进行，第 1 步，设定某一敷设方式下电缆群的温度场分布；第 2 步，在完成电缆群温度场分布求解的前提下，利用Matlab优化设计技术，调用合适的优化算法，设置必要的优化步骤，计算电缆群的最优化电流分布。

1）设计变量（DVs）。设计过程中需要不断调整赋值的变量参数。每个设计变量可能有上、下限，用于规定其取值范围。本文中的设计变量为每条敷设电缆的实时载流量。

2）状态变量（SVs）。即设计要求满足的约束条件变量参数，它是设计的因变量，是设计变量的函数。本文中的状态变量为电缆群的实时载流量之和。

1.2  电缆群载流量优化数值计算模型

电缆群载流量优化的目标是使电缆群的总载流量（即所有电缆的电流之和）最大，电缆群中不同的电缆电流分布可以看作不同的设计方案，即电缆群中不同的电缆电流组合构成不同的设计方案。

把电缆群中各根电缆电流作为优化设计变量，在优化过程中，可以不断调整电流的赋值；把各根电缆线芯温度作为状态变量，线芯温度是电缆电流的函数，并设定线芯温度上限值不超过 90 ℃，这是利用改进的灰狼算法计算电缆载流量的依据。

因为状态变量为电缆群的实时载流量之和。因此在进行目标函数的设定时，需要将其考虑与其中。本文代价函数的性能指标可以设定为：

该目标函数是电缆电流的函数，目标函数取得最小值的设计方案就是最优化设计方案，此时电缆群的所有电缆电流之和达到最大。

2  基于改进的灰狼算法

2.1 灰狼算法基础理论（GWO）

灰狼算法的灵感是源自动物界中的灰狼群体。灰狼算法中，拥有 最优适应度值的三匹狼分别被定义为 狼、 狼和 狼，并作为领导群体，影响种群中其他狼的位置的更新，种群中的剩余个体被定义为 狼。

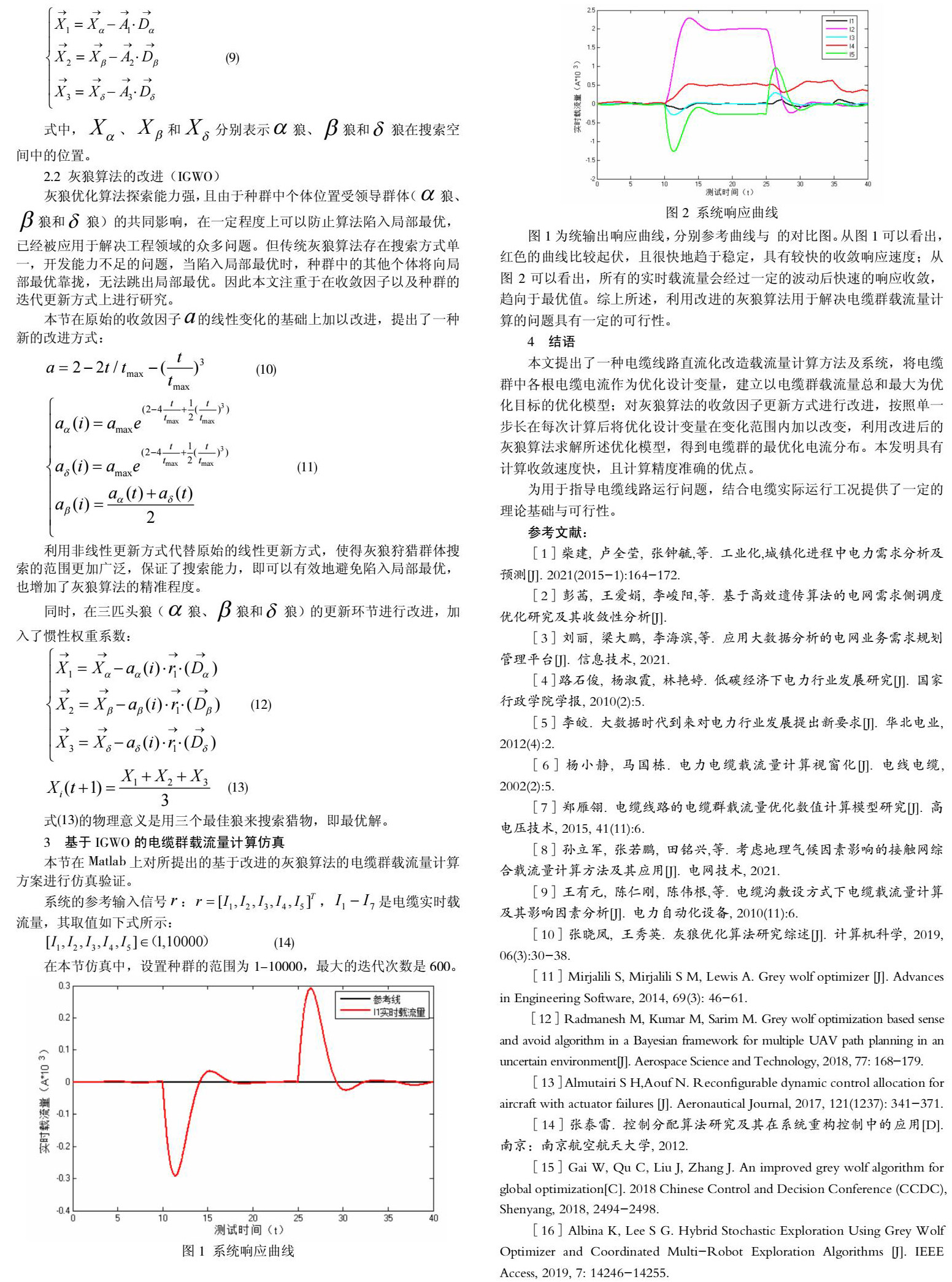
图1为统输出响应曲线，分别参考曲线与 的对比图。从图1可以看出，红色的曲线比较起伏，且很快地趋于稳定，具有较快的收敛响应速度；从图2可以看出，所有的实时载流量会经过一定的波动后快速的响应收敛，趋向于最优值。综上所述，利用改进的灰狼算法用于解决电缆群载流量计算的问题具有一定的可行性。

4  结语

本文提出了一种电缆线路直流化改造载流量计算方法及系统，将电缆群中各根电缆电流作为优化设计变量，建立以电缆群载流量总和最大为优化目标的优化模型；对灰狼算法的收敛因子更新方式进行改进，按照单一步长在每次计算后将优化设计变量在变化范围内加以改变，利用改进后的灰狼算法求解所述优化模型，得到电缆群的最优化电流分布。本发明具有计算收敛速度快，且计算精度准确的优点。

为用于指导电缆线路运行问题，结合电缆实际运行工况提供了一定的理论基础与可行性。

参考文献：

［1］ 柴建， 卢全莹， 张钟毓，等. 工业化，城镇化进程中电力需求分析及预测[J]. 2021（2015-1）：164-172.

［2］ 、彭茜， 王爱娟， 李峻阳，等. 基于高效遗传算法的电网需求侧调度优化研究及其收敛性分析[J].

［3］ 刘丽， 梁大鹏， 李海滨，等. 应用大数据分析的电网业务需求规划管理平台[J]. 信息技术， 2021.

［4］ 路石俊， 杨淑霞， 林艳婷. 低碳经济下电力行业发展研究[J]. 国家行政学院学报， 2010（2）：5.

［5］ 李皎. 大数据时代到来对电力行业发展提出新要求[J]. 华北电业， 2012（4）：2.

［6］ 杨小静， 马国栋. 电力电缆载流量计算视窗化[J]. 电线电缆， 2002（2）：5.

［7］ 郑雁翎. 电缆线路的电缆群载流量优化数值计算模型研究[J]. 高电压技术， 2015， 41（11）：6.

［8］ 孙立军， 张若鹏， 田铭兴，等. 考虑地理气候因素影响的接触网综合载流量计算方法及其应用[J]. 电网技术， 2021.

［9］ 王有元， 陈仁刚， 陈伟根，等. 电缆沟敷设方式下电缆载流量计算及其影响因素分析[J]. 电力自动化设备， 2010（11）：6.

［10］ 张晓凤， 王秀英. 灰狼优化算法研究综述[J]. 计算机科学， 2019， 06（3）：30-38.

［11］ Mirjalili S， Mirjalili S M， Lewis A. Grey wolf optimizer [J]. Advances in Engineering Software， 2014， 69（3）： 46-61.

［12］ Radmanesh M， Kumar M， Sarim M. Grey wolf optimization based sense and avoid algorithm in a Bayesian framework for multiple UAV path planning in an uncertain environment[J]. Aerospace Science and Technology， 2018， 77： 168-179.

［13］ Almutairi S H， Aouf N. Reconfigurable dynamic control allocation for aircraft with actuator failures [J]. Aeronautical Journal， 2017， 121（1237）： 341-371.

［14］ 张泰雷. 控制分配算法研究及其在系统重构控制中的应用[D]. 南京：南京航空航天大学， 2012.

［15］ Gai W， Qu C， Liu J， Zhang J. An improved grey wolf algorithm for global optimization[C]. 2018 Chinese Control and Decision Conference （CCDC）， Shenyang， 2018， 2494-2498.

［16］ Albina K， Lee S G. Hybrid Stochastic Exploration Using Grey Wolf Optimizer and Coordinated Multi-Robot Exploration Algorithms [J]. IEEE Access， 2019， 7： 14246-14255.