打开文本图片集

单元复习课是帮助学生复习近期所学，承载着将碎片化的单元知识结构化、系统化，数学思想方法深入化的功能。基于“串联”策略的复习课可以横纵关联，引导学生走向整体思考。笔者以《对称图形——圆》单元复习展示课为例，阐述自己的思考。

1 备课思考

《对称图形——圆》是苏科版教材九年级上册第2章内容，是继三角形、四边形之后又一个重点研究的图形，主要内容有：基本性质、与圆有关的位置关系、正多边形与圆、与圆有关的计算。虽然学生已经通过新授课进行了系统地学习，但由于圆章节教学时间长，内容繁多，容易造成知识前学后忘，知识点碎片化，“只见木不见林”。基于“串联”的复习策略，能有效帮助学生回顾旧知，逐步建构知识网络，易于形成整体认知。

2 教学目标

（1）经历运用平移变换建构知识的过程，体会知识间的整体联系，形成清晰的章知识脉络。

（2）掌握圆的基本性质，点与圆、直线与圆的位置关系的判定与性质，正多边形与圆的关系以及与圆有关的计算，在解决问题中获得解题经验。

（3）在解决与圆有关的问题中，学会有条理地思考与表达，感悟数形结合思想、转化思想、分类讨论等思想。

3 教学过程

3.1 操作活动，导入复习

活动 同学们已经学习过平移、翻折、旋转变换，请分别对圆进行翻折、旋转，并思考问题：圆具有哪些对称性？

师生活动：学生动手操作，教师通过询问“你是怎样折的？”，学生能够说出沿着直径翻折、绕着圆心旋转，从而回忆起圆具有轴对称性和中心对称性。

设计意图：通过简单地折纸操作，既促使学生自然回忆起圆的两种对称性，同时也为圆的基本性质的复习定好基调，一石二鸟。

3.2 基于“串联”，展开复习

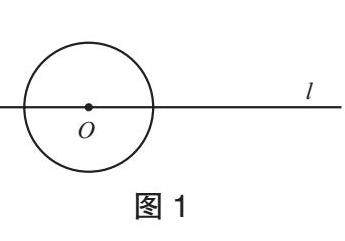
问题1 如图1，圆心O在直线l上，已知O的半径为5，现将O沿直线l向右平移3个单位长度到M的位置，那么点O与M有怎样的位置关系？

师生活动：学生思考后回答，教师追问：如何判定点与圆的位置关系？引导学生说出用“数量关系判定位置关系”的方法。

设计意图：通过圆的初次平移，让学生总结出判定点与圆位置关系的方法，体会数形结合思想。

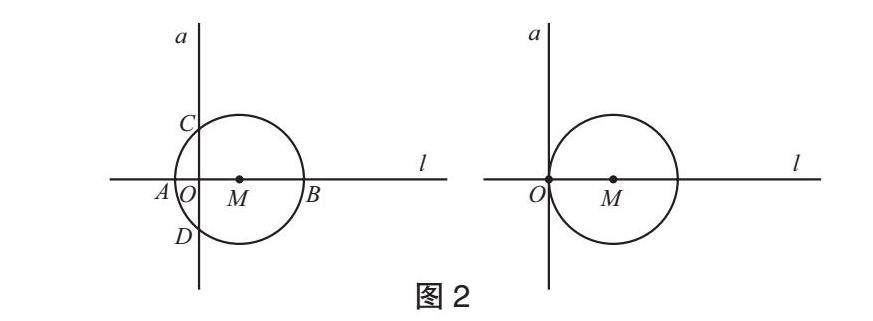
问题2 如图2，过点O作直线l的垂线a，你能求出图中哪些线段的长？如果要使M与直线a相切，M还需向右平移几个单位长度？说说你的理由。

师生活动：学生通过构造半径CM，运用勾股定理可求出OC长，进而利用垂径定理求出CD长。教师引导学生说出，在运用垂径定理时，通常要构造“半径、半弦、弦心距”组成的直角三角形，通过勾股定理建立方程解决问题。对于第2个问题，教师追问：“怎样判断直线a是圆的切线？有其他的方法吗？”，帮助学生厘清切线的判定方法。

设计意图：通过设计过点O的垂线，引导学生回顾垂径定理的内容与基本方法。通过第2次平移，把学生的视角自然地拉到直线与圆的位置关系上来，引导学生总结出特殊的位置关系（相切）的判定方法：①用数量关系判定位置关系；②切线的判定定理。

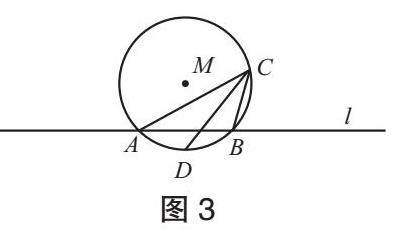
问题3 将M继续平移到如图3所示的位置，M交x轴于A，B两点，AB=5，连接CA，CB， ∠ACB的平分线交M于点D，你能求出哪些角的度数？图中有哪些相等的量？

追问：（1）你是根据什么知识得到∠ACB=45°的？ 圆心角和圆周角之间是通过什么元素相互建立联系的？（2）“弧AD与弧DB相等”是根据什么知识得到的？

设计意图：通过第3次平移，适当添加圆周角以及它的角平分线，帮助学生回顾圆周角定理、等对等定理的内容，并通过追问，提炼出两个定理的核心思想方法。

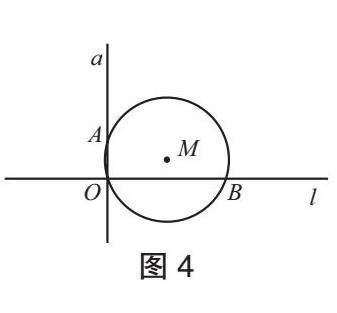
问题4 如图4，继续平移M，使得M过点O，OA=2， 你能求出OB的长吗？

设计意图：通过第4次平移，使得直角顶点在圆周上，从而得到弦AB是直径，AB=10，引导学生回顾圆周角定理的推论。

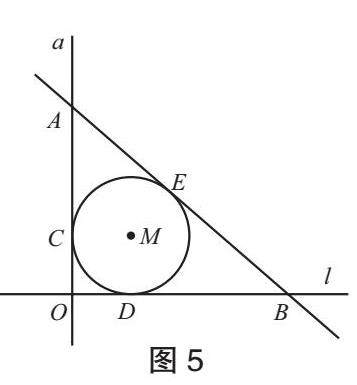
问题5 如图5，将M缩小后，继续平移，使得M与x轴、y轴相切于点C，D，直线AB也与M相切，切点为E， 若AE=4， BE=6， 那么M的半径为多少？

设计意图：改变M的大小后，第5次平移，使其与直线a，l都相切，再添加一条切线AB，让M成为直角三角形AOB的内切圆。在计算内切圆半径的过程中，学生可以用勾股定理建立方程解决问题，也可以用等面积法建立方程解决问题，但两种方法都需要运用到切线长定理结论，从而自然过渡到对切线长定理的复习。

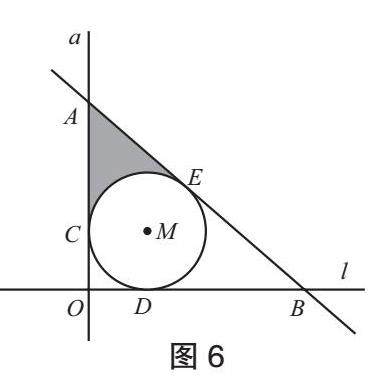
问题6 如图6，如何求阴影部分的面积？说说你的方法。

追问：怎样求不规则图形的面积？扇形的面积如何求？师生共同总结出求不规则图形面积的方法。

设计意图：在问题5的基础上对不规则图形区域阴影化处理，自然过渡到与圆有关的计算板块的复习，其中渗透转化的数学思想。这里只需厘清方法、回忆公式即可，不要求学生进行具体计算。

由以上6个问题逐渐形成以下章节脉络：

3.3查漏补缺，完善知识网络

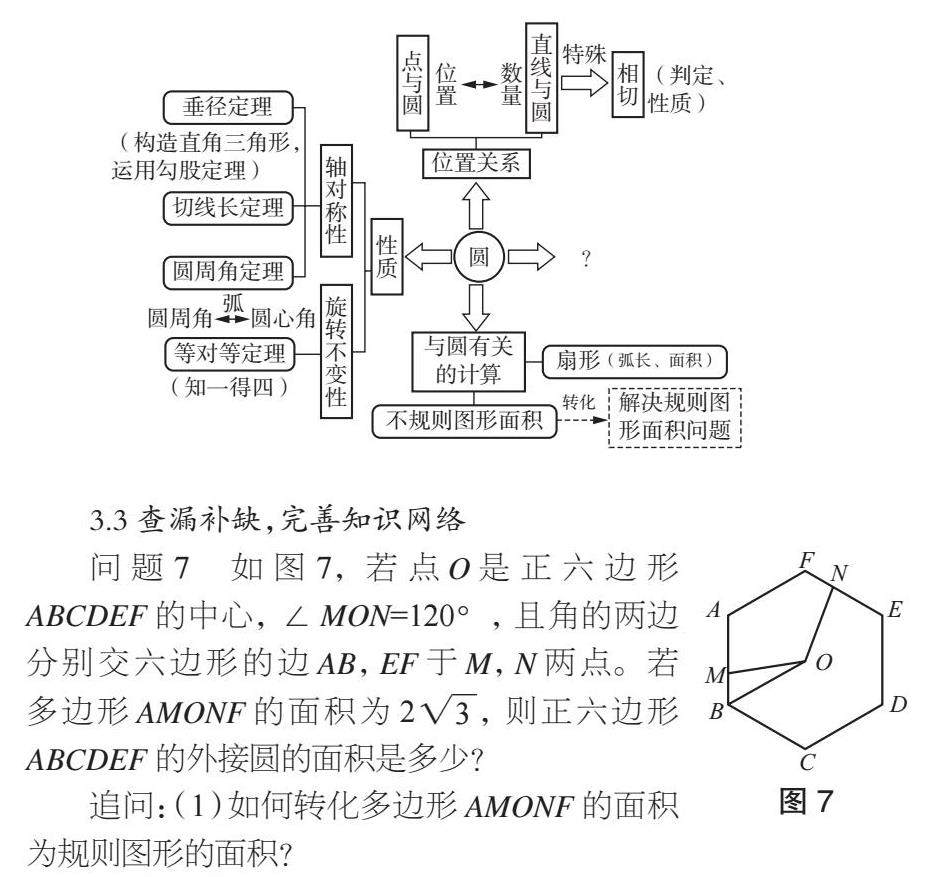
问题7 如图7，若点O是正六边形ABCDEF的中心， ∠MON=120°，且角的两边分别交六边形的边AB，EF于M，N两点。若多边形AMONF的面积为2，则正六边形ABCDEF的外接圆的面积是多少？

追问：（1）如何转化多边形AMONF的面积为规则图形的面积？

（2）正多边形与圆有怎样的关系？如何解决正多边形问题？

设计意图：本题涉及正多边形与圆的关系、三角形全等的判定、菱形的判定以及等边三角形面积计算等知识点，学生要运用转化思想将多边形的面积转化为菱形的面积，菱形面积再转化为正三角形面积， 在解决问题的过程中，体会“等分圆得到正多边形”这一关系，教师帮助学生补齐最后一版块的知识结构：

3.4综合运用，拓展能力，提升素养

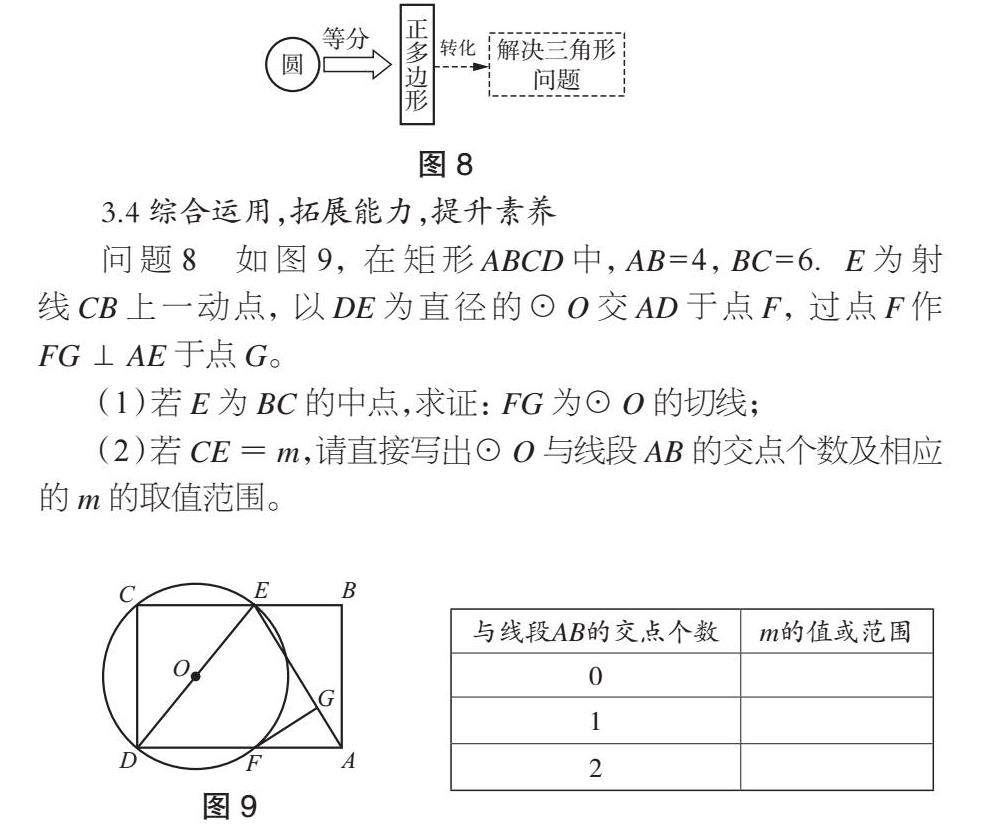
问题8 如图9，在矩形ABCD中，AB=4，BC=6．E为射线CB上一动点，以DE为直径的⊙O交AD于点F，过点F作FG⊥AE于点G。

（1）若E为BC的中点，求证：FG为⊙O的切线；

（2）若CE＝m，请直接写出⊙O与线段AB的交点个数及相应的m的取值范围。

师生活动：学生先独立思考，想象相关图形，如有困难，教师展示几何画板动态演示，要求学生画出特殊位置的图形，小组讨论后填写表格。

设计意图：在已经横向“串联”构建起章知识网络的基础上，纵向提升学生分析、解决问题的能力。由于圆章节重点内容较多，这里侧重于研究直线与圆的位置的关系，引导学生感悟分类讨论思想，培养学生有条理地表达，几何直观、推理等数学素养。

4 教学反思

4.1 基于“串联”，构建知识网络

章建跃博士曾说：“教学要有贯穿课堂始终的主线，要有结构的、逻辑关联、层层递进且能启迪学生思维的问题引领……”。数学是一个整体，复习教学应引导学生把知识点连成线，织成网，在头脑中形成知识体系，这样的复习有利于学生全面认识和准确理解相关的数学知识。本节课从关联的视角重新审视复习内容，有效整合已有知识，通过5次平移进行“串联”，构建了知识网络，系统高效地复习了圆章节的大部分知识，引导学生理解性质、判定方法，提升学生分析问题、解决问题的能力。

4.2 走向“整体”，发展一般观念

《义务教育数学课程标准（2022年版）》指出，数学教学要帮助学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展核心素养。纵观本章可以发现，研究圆的性质其实就是研究基本元素（圆心、半径）与相关要素（弦、弧、圆心角、圆周角等）之间的关系；研究点与圆、直线与圆的位置关系时都是用数量关系来刻画；研究与圆有关的计算就是研究整体（圆）与部分（扇形），平面（扇形）与曲面（圆锥）的相互依存转化关系。也就是说，圆的研究延续和发展了三角形、四边形的研究思路，这有利于学生形成对图形知识研究的整体思维和一般观念，也有利于更好地发展核心素养。